BCI代数的Ω-犹豫模糊P理想

姜 曼

(西安交通工程学院 公共课部,西安 710300)

0 引 言

自从模糊集[1]的概念被提出后,模糊集已经应用到生活中的各个方面.模糊集及其扩展在处理问题中的不确定性方面取得了成功的结果,在世界范围内,人们对模糊集的应用兴趣正在迅速增长.由于需要考虑元素之间非此即彼的关系,文献[2]提出了直觉模糊集;由于在客观事物都具有两极性,在处理问题中难免有更多的不确定性,文献[3]提出了双极值模糊集的概念;Ω-模糊集[4]是经典凸集的推广,它是线性空间中一类特殊的模糊集;为了能够更全面,更精确地了解决策者对信息的判断,文献[5]提出了犹豫模糊集.直觉模糊集和双极值模糊集已经得到推广,这些模糊化思想也被应用到其他代数结构中,一系列结论相继出现,例如,文献[6]研究了否定非对合剩余格中的双极值模糊理想并讨论了它们的性质,文献[7]把直觉模糊理论和教学评价相结合做的一些研究,更多结论见文献[8-9].

犹豫模糊集是一种表达现实生活中人们在决策中模棱两可的有用工具,它解决了很多不确定性问题.它在解决问题时比一般的模糊集更精准,能够解决一些存在犹豫性的,不确定的问题,这在许多数学模型中都有应用[10-12].犹豫模糊集的思想更接近于一般思维,能更准确地研究逻辑代数.文献[13-14]提出了Baltic Capesize Index Algebras(简称BCI代数),并在BCI代数中引入了模糊 Prime Ideal(简称P理想)的概念,BCI代数是逻辑代数的一个典型代表,它上面的准则,比如滤子、子代数、理想等都有很强的研究意义.因此,本文主要研究BCI代数中的Ω-犹豫模糊P理想,得到了一些有意义的结果.

1 预备知识

1.1 BCI代数

定义1[13]对一个集合X,如果它满足下列条件:对∀x,y,z∈X,有

(i) {(x*y)*(x*z)}*(z*y)=0; (ii) {x*(x*y)}*y=0; (iii)x*x=0;

(iv)x*y=y*x=0⟹x=y; (v)x*0=0⟹x=0,

则称集合X为BCI代数.

定义2[13]设X是BCI-代数,I是X上的非空子集,如果I满足以下条件:

(vi) 0∈I; (vii) ∀x,y∈X,x*y∈I和y∈I,x∈I,

则称I是X上的理想.

在本文中,用Ω和X表示BCI代数上的非空集合.

定义3[13-15]μ是X上的模糊集,如果∀x,y∈X,μ满足下列条件:

(viii)μ(0)≥μ(x); (ix)μ(x)≥μ(x*y)∧μ(y),

则称μ是X上的模糊理想.

定义4[15]设I是X上的非空子集,∀x,y∈X,如果μ满足下列条件:

(vi) 0∈I; (x)(x*z)*(y*z)∈I和y∈I,x∈I,

则称μ是X上的P理想.

定义5[15]μ是X上的模糊集,∀x,y,z∈X,如果μ满足(viii)和下列条件:

(xi)μ(x)≥μ((x*z)*(y*z))∧μ(y),

则称μ是X上的模糊P理想.

定义6[5]设Ω,X表示一非空集合,称映射δ∶R×Ω→[0,1]为R的Ω-模糊集.

定义7[16]δ是X上的Ω-模糊集,如果∀x,y∈X,q∈Ω,δ满足下列条件:

(xii)δ(0,q)≥δ(x,q); (xiii)δ(x,q)≥δ(x*y,q)∧δ(y,q),

则称δ是X上的Ω-模糊P理想.

性质1[15]设X是BCI代数,则有

(xiv)0*(0*((x*z)*(y*z)))=(0*y)*(0*x);

(xv)0*(0*((x*y))=(0*y)*(0*x).

1.2 犹豫模糊集

定义8[5]设X是一个给定集合,一个X上的犹豫模糊集A的定义如下:A∶{(x,hA(x))|x∈X},其中hA(x)是由区间[0,1]上若干个不同值构成的集合,表示X中的元素x属于集合A的若干种可能隶属度.记X上的全体犹豫模糊集为HF(X).

如果P([0,1])为区间[0,1]的幂集,A为X上的犹豫模糊集.称集合X(A,γ)∶={x∈X|γ⊆hA(x)}为A的犹豫水平集,并且γ∈P([0,1]).

2 Ω-犹豫模糊P理想

定义9设X上的Ω-犹豫模糊集A具有如下形式:A∶{(x,hA(x,q))|x∈X,q∈Ω}.

记X上的全体Ω-犹豫模糊集为Ω-HF(X).

定义10设A∈HF(X),对∀x,y,z∈X,如果A满足以下条件:

(i)hA(0)⊇hA(x);

(ii)hA(x)⊇hA((x*z)*(y*z))∩hA(y),

则称A是X的犹豫模糊P理想.记X的全体犹豫模糊P理想为HFPI(X).

定义11设A∈Ω-HF(X),对∀x,y,z∈X,q∈Ω,如果A满足以下条件:

(iii)hA(0,q)⊇hA(x,q);

(iv)hA(x,q)⊇hA((x*y),q)∩hA(y,q),

则称A是X的Ω-犹豫模糊理想.记X的全体犹豫模糊理想为Ω-HFI(X).

定义12设A∈Ω-HF(X),对∀x,y,z∈X,∀q∈Ω,如果A满足以下条件:

(iii)hA(0,q)⊇hA(x,q);

(v)hA(x,q)⊇hA((x*z)*(y*z),q)∩hA(y,q),

则称A是X的Ω-犹豫模糊P理想.记X上全体Ω-犹豫模糊P理想为Ω-HFPI(X).

例1(i) 每一个常数函数A∶X×Ω→[0,1]是X的Ω-犹豫模糊P理想.

(ii) 令X={0,a,b,c}是一个BCI代数,且满足下表:

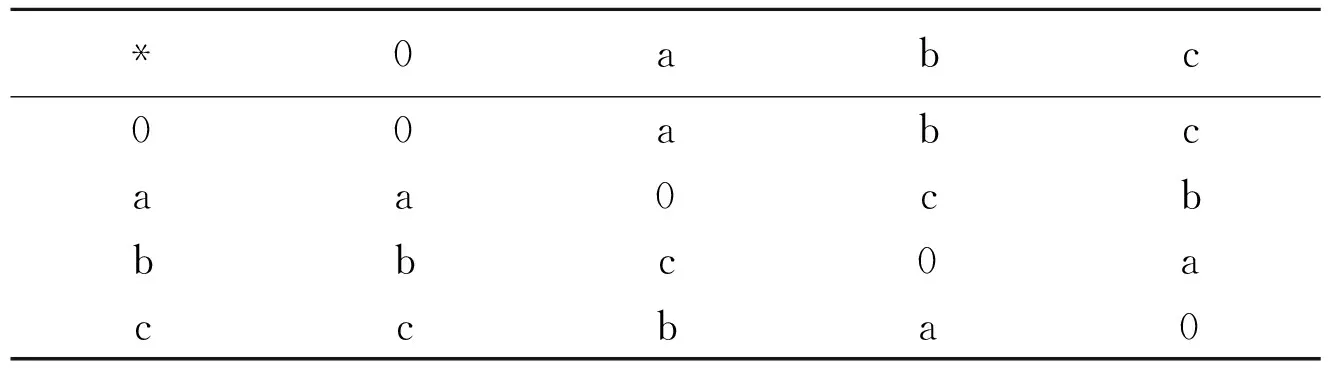
表1 BCI代数

定义X上的Ω-犹豫模糊集如下:对任意的q∈Ω,hA(0,q)=0.8,hA(a,q)=0.6,hA(b,q)=hA(c,q)=0.5;通过计算可得A是X的Ω-犹豫模糊P理想.

性质2若A∈Ω-HF(X),A∈Ω-HFPI(X).如果对∀x,y∈X,且x≤y,那么有hA(x,q)⊇hA(y,q).

性质3设A∈Ω-HFPI(X),如果∀x∈X,q∈Ω,则有hA(x,q)⊇hA(0*(0*x),q)成立.

证因为A∈Ω-HFPI(X),则对∀x,y,z∈X,∀q∈Ω,有

hA(x,q)⊇hA((x*z)*(y*z),q)∩hA(y,q),

现在用x代替z,用0代替y,则有

hA(x,q)⊇hA((x*x)*(0*x),q)∩hA(0,q)=hA(0*(0*x),q)∩hA(0,q)=hA(0*(0*x),q).

定理1如果A∈Ω-HFPI(X),则A∈Ω-HFI(X).

证令A∈Ω-HFPI(X).对∀x,y∈X,∀q∈Ω,由于x*0=x,则有

hA(x,q)⊇hA((x*0)*(y*0),q)∩hA(y,q)=hA(x*y,q)∩hA(y,q).

因此,A∈Ω-HFI(X).

注 定理1的逆,即如果A是X上的Ω-犹豫模糊理想,不能得到A是X上的Ω犹豫模糊P理想,下面给出具体例子说明此结论.

例2令X={0,a,b,c,d}是一个BCI代数,满足下表:

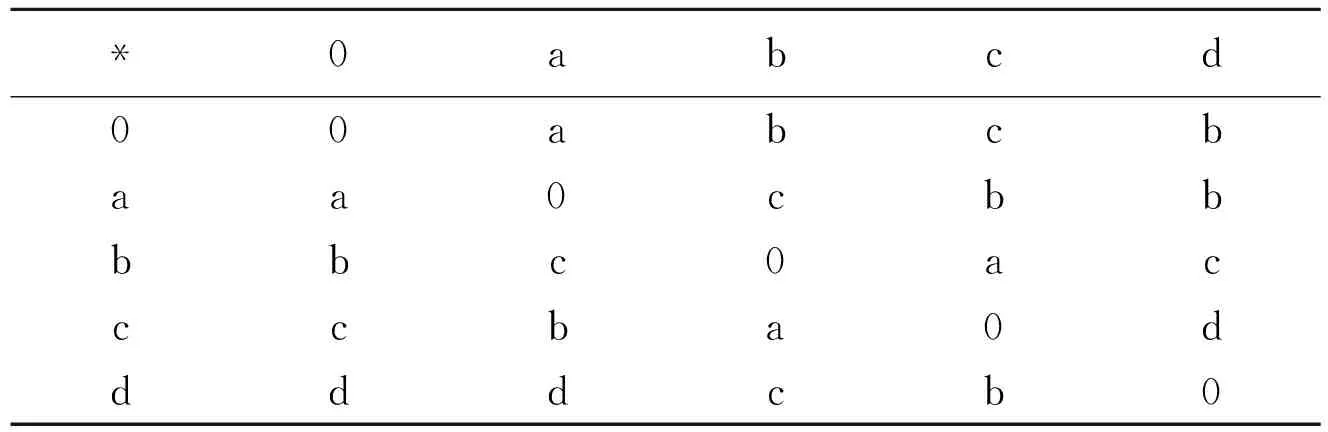
表2 BCI代数

定义X上的Ω-犹豫模糊集如下:A∶X×Ω→[0,1],且对任意的q∈Ω,令

hA(0,q)=0.71,hA(a,q)=0.62,hA(b,q)=hA(c,q)=hA(c,q)=0.58;

根据计算可得A∈Ω-HFI(X).但是

hA(a,q)⊂hA((a*b)*(0*b),q)∩hA(0,q),

因此A∉Ω-HFPI(X).

定理2设A∈Ω-HFPI(X),如果对∀x,y,z∈X,∀q∈Ω,则hA((x*z)*(y*z),q)⊇hA(x*y,q)成立.

证在BCI代数中有(x*z)*(y*z)≤x*y成立,则有

((x*z)*(y*z))*(x*y)=0.

因为A∈Ω-HFPI(X),则由定理1可得A∈Ω-HFI(X).即对∀x,y,z∈X,∀q∈Ω,有

hA((x*z)*(y*z),q)⊇hA(((x*z)*(y*z))*(x*y),q)∩hA(x*y,q)
=hA(0,q)∩hA(x*y,q)=hA(x*y,q).

定理3设A∈Ω-HFI(X),如果对∀x,y,z∈X,∀q∈Ω,有

hA((x*y)*(y*z),q)⊆hA(x*y,q)

成立,则有A∈Ω-HFPI(X).

证因为A∈Ω-HFI(X),对∀x,y,z∈X,∀q∈Ω,则有

hA((x*z)*(y*z),q)∩hA(y,q)⊆hA(y,q)∩hA(x*y,q)⊆hA(x,q)

和定义11(iii)成立,因此,A∈Ω-HFPI(X).

说明 若A∈Ω-HFI(X),则有hA(0*(0*x),q)⊇hA((0*(0*x))*x,q)∩hA(x,q).

定理4如果A∈Ω-HFI(X),则对∀x∈X,∀q∈Ω,有hA(x,q)⊆hA(0*(0*x),q)成立.

证若A∈Ω-HFI(X),则对∀x∈X,∀q∈Ω,有

hA(0*(0*x),q)⊇hA(0*(0*x)*x,q)∩hA(x,q)=hA(0,q)∩hA(x,q)=hA(x,q)

成立.

定理5设A∈Ω-HFI(X),如果对∀x∈X,∀q∈Ω,有hA(x,q)⊇hA(0*(0*x),q)成立,则有A∈Ω-HFPI(X).

证对∀x,y,z∈X,∀q∈Ω,因为A∈Ω-HFI(X),由定理4以及性质1,有

hA((x*z)*(y*z),q)⊆hA(0*(0*((x*z)*(y*z))),q)=hA((0*y)*(0*x),q)
=hA(0*(0*(x*y)),q)⊆hA(x*y,q).

因此,由定理3可得,A∈Ω-HFPI(X).

定理6设A,B∈Ω-HF(X) ,如果A,B∈Ω-HFPI(X),则A∩B∈Ω-HFPI(X).

证由于A,B∈Ω-HFPI(X),因此对∀x,y,z∈X,∀q∈Ω,则

hA∩B(0,q)=hA(0,q)∩hB(0,q)⊇hA(x,q)∩hB(x,q)=hA∩B(x,q),

hA∩B(x,q)=hA(x,q)∩hB(x,q)

⊇(hA((x*z)*(y*z),q)∩hA(y,q))∩(hB((x*z)*(y*z),q)∩hB(y,q))

=(hA((x*z)*(y*z),q)∩hB((x*z)*(y*z),q))∩(hA(y,q)∩hB(y,q))

=hA∩B((x*z)*(y*z),q)∩hA∩B(y,q).

定义13设X和X′都是BCI代数,f是X到X′的同态映射,A与B分别是X和X′上的Ω-犹豫模糊集,则由f可以诱导出两个Ω-犹豫模糊集f(A)和f-1(B):

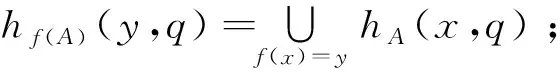
定理7X,X′是两个BCI代数,设f∶X→X′是同态满射,B∈Ω-HF[X′],如果B∈Ω-IFPI[X′],则有f-1(B)∈Ω-IFPI[X].

证设

B={x,hB(x,q)|x∈X′,q∈Ω},f-1(B)={x,hf-1(B)(y,q)|x,y∈X′,q∈Ω}.

由于B∈Ω-IFPI[X′],因此对∀x∈X,∀q∈Ω,有

hf-1(B)(0,q)=hB(f(0),q)=hB(0′,q)⊇hB(f(x),q)=hf-1(B)(x,q),

对∀y′,z′∈X′,∀q∈Ω.因为f∶X→X′是同态满射,所以∃y,z∈X,使得f(y)=y′,f(z)=z′.则有

hf-1(B)(x,q)⊇hB((f(x)*z′)*(y′*z′),q)∩hB(y′,q)

=hB((f(x)*f(z))*(f(y)*f(z)),q)∩hB(f(y),q)

=hB(f((x*z)*(y*z)),q)∩hB(f(y),q)

=hf-1(B)((x*z)*(y*z),q)∩hf-1(B)(y,q),

因此f-1(B)∈Ω-IFPI[X].

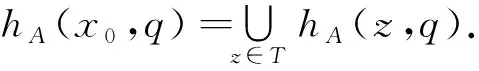
定理8X,X′是两个BCI代数,设f∶X→X′是同态满射,若A具有上确界且满足A∈Ω-HFPI[X],则有f(A)∈Ω-HFPI[X′].

证设

A={x,hA(x,q))|x∈X,q∈Ω},

f(x)={y,hf(x)(y,q)|f(x)=y,y∈X,q∈Ω}.

由于0∈f-1(0′),则对∀x∈X,∀q∈Ω,有

对∀x′∈X′,∀q∈Ω,有

对∀x′,y′,z′∈X′,∀q∈Ω,令x0∈f-1(x′),y0∈f-1(y′),z0∈f-1(z′),则有

因此可得

综上可得,f(A)∈Ω-HFPI[X′].

现在,研究如何用犹豫模糊P理想构造Ω犹豫模糊P理想.

定理9X是一个BCI代数,令Ω={A|A∈HFPI(X)},定义B∈Ω-HF(X),如果对∀x∈X,∀B∈Ω,hB(x,A)=hA(x), 则B∈Ω-HFPI(X).

证∀x∈X,∀A∈Ω,则有

hB(0,A)=hA(0)⊇hA(x)=hB(x,A).

∀x,y,z∈X,∀A∈Ω,可得

hB(x,A)=hA(x)⊇hA((x*z)*(y*z))∩hA(y)=hB((x*z)*(y*z),A)∩hB(y).

因此,B∈Ω-HFPI(X).

定义XΩ∶Ω→X,在XΩ上定义二元运算⊗:

(α⊗β)(q)=α(q)*β(q),α,β∈XΩ,q∈Ω,

则(XΩ,⊗,θ)是一个BCI代数,且对q∈Ω,θ是XΩ上的零映射当且仅当θ(q)=0.

定理10设A∈HFPI(X),如果f∶XΩ×Ω→[0,1],其中hf(α,q)=hA(α(q)),α∈XΩ,q∈Ω.则f∈Ω-HFPI(XΩ).

证对α,β,γ∈XΩ,q∈Ω,有

hf(α,q)=hA(α(q))⊇hA(0)=hA(θ(q))=hf(θ,q),

hf(α,q)=hA(α(q))⊇hA((α(q)*γ(q))*(β(q)*γ(q)))∩hA(β(q))

=hA((α⊗γ)(q)*(β⊗γ)(q))∩hA(β(q))

=hA((α⊗γ)⊗(β⊗γ))(q))∩hA(β(q))

=hf((α⊗γ)⊗(β⊗γ),q)∩hf(β,q),

因此f∈Ω-HFPI(XΩ).

定理11令A∈Ω-HFPI(XΩ),对∀q∈Ω,定义Aq∶X→[0,1],其中对∀x∈X,hAq(x)=hA(x,q).则有Aq∈Ω-HFPI(X).

证对∀x∈X,∀q∈Ω,有

hAq(0)=hA(0,q)⊇hA(x,q)=hAq(x).

令x,y,z∈X,q∈Ω,则

hAq(x)=hA(x,q)⊇hA((x*z)*(y*z),q)∩hA(y,q)=hAq((x*z)*(y*z))∩hAq(y),

因此,Aq∈Ω-HFPI(X).

定理12令A∈Ω-HF(X),A∈Ω-HFPI(X)当且仅当对∀γ∈[0,1],则有

R(A,γ)={x∈X|hA(x,q)⊇γ,q∈Ω}≠∅

是X的P理想.

证假设A∈Ω-HFPI(X),由定义12可得,对∀x∈X,q∈Ω,hA(0,q)⊇hA(x,q).因此,hA(0,q)⊇hA(x,q)⊇γ,所以0∈R(A,γ).

令(x*z)*(y*z)∈R(A,γ),y∈R(A,γ),则

hA((x*z)*(y*z),q)⊇γ,hA(y,q)⊇γ.

因为A∈Ω-HFPI(X),则有

hA(x,q)⊇hA((x*z)*(y*z),q)∩hA(y,q)⊇γ,

因此A∈Ω-HFPI(X).

反之,仅需要证明定义12中的(i)和(ii)成立.用反证法证明.

假设(i)不成立.则存在x′∈X,q′∈Ω,使得

hA(x′,q′)⊃hA(0,q′).

如果令γ′=[hA(x′,q′)+hA(0,q′)]/2,则有hA(x′,q′)⊃γ′⊃hA(0,q′).因此x′∈A且R(A,γ)≠∅.因为R(A,γ)是X的P理想,则有0∈R(A,γ),因此γ′⊆hA(0,q′).产生矛盾.

假设(ii)不成立.则存在x′,y′,z′∈X,q′∈Ω,有

hA(x′,q′)⊂hA((x′*z′)*(y′*z′),q′)∩hA(y′,q′).

令

γ′=[hA(x′,q′)+hA((x′*z′)*(y′*z′),q′)∩hA(y′,q′)]/2,

则

hA(x′,q′)⊂γ′⊂hA((x′*z′)*(y′*z′),q′)∩hA(y′,q′),

因此可得

γ′⊂hA((x′*z′)*(y′*z′),q′),γ′⊂hA(y′,q′),

即(x′*z′)*(y′*z′)∈R(A,γ),y′∈R(A,γ).因为R(A,γ)是X的P理想,则有x′∈R(A,γ),并且hA(x′,q′)⊇γ′.这仍然矛盾.

定理13若A∈Ω-HFPI(X),则对∀x0∈X,Ix0={x∈X|hA(x,q)⊇hA(x0,q),q∈Ω}≠∅是X的P理想.

Ix0={x∈X|hA(x,q)⊇hA(x0,q),q∈Ω}

是X的P理想.

3 Ω-犹豫模糊P理想的乘积

定义14设ξ是X上的一个Ω-犹豫模糊关系,则称ξ是X×X上的Ω犹豫模糊集.其中ξ定义如下:ξ∶(X×X)×Ω→[0,1].

定义15设A,B∈Ω-HF(X),对∀x,y∈X,q∈Ω,A和B的乘积A×B定义如下:

hA×B((x,y),q)=hA(x,q)∩hB(y,q).

引理1令A,B∈Ω-HF(X),则以下结论成立:

(i)A×B是X上的Ω-犹豫模糊关系;(ii)∀t∈[0,1],(A×B)t=At×Bt.

定义16设A∈Ω-HF(X),则X上的强Ω-犹豫模糊关系ξ0是X×X上的Ω犹豫模糊集,且ξ0定义如下:hξ0((x,y),q)=hA(x,q)∩hB(y,q),∀x,y∈X,q∈Ω.

引理2设A∈Ω-HF(X),如果ξ0是X上的强Ω-犹豫模糊关系,则对∀t∈[0,1],有(ξ0)t=At×At.

定理14设A∈Ω-HF(X),ξ0是X上的强Ω-犹豫模糊关系.如果ξ0是X×X上的Ω犹豫模糊P理想,则对∀x∈X,q∈Ω,有hA(0,q)⊇hA(x,q)成立.

证因为ξ0是X×X上的Ω犹豫模糊P理想,即对∀x∈X,q∈Ω,hξ0((0,0),q)⊇hξ0((x,x),q).因此

hA(0,q)∩hA(0,q)⊇hA(x,q)∩hA(x,q),

由此可得hA(0,q)⊇hA(x,q).

定理15令A,B∈Ω-HFPI(X),则A×B∈Ω-HFPI(X×X).

证对∀(x,y)∈X×X,q∈Ω,由于A,B∈Ω-HFPI(X),首先

hA×B((0,0),q)=hA(0,q)∩hB(0,q)⊇hA(x,q)∩hB(y,q)=hA×B((x,y),q).

又令(x1,x2),(y1,y2),(z1,z2)∈X×X,q∈Ω,则有

hA×B(((x1,x2)*(z1*z2))*((y1,y2)*(z1*z2)),q)∩hA×B((y1,y2),q)

=hA×B(((x1*z1,x2*z2)*(y1*z1,y2*z2),q)∩hA×B((y1,y2),q)

=hA×B(((x1*z1)*(y1*z1),(x2*z2)*(y2*z2)),q)∩hA×B((y1,y2),q)

=hA(((x1*z1)*(y1*z1),q)∩hB((x2*z2)*(y2*z2),q)∩hA(y1,q)∩hB(y2,q)

=hA((x1*z1)*(y1*z1),q)∩hA(y1,q)∩hB((x2*z2)*(y2*z2),q)∩hB(y2,q)

⊆hA(x1,q)∩hB(y1,q)=hA×B((x1,y1),q).

即证A×B∈Ω-HFPI(X×X).

定理16A,B∈Ω-HF(X),如果A×B∈Ω-HFPI(X×X),则以下结论成立:

(i) ∀x∈X,q∈Ω,hA(x,q)⊆hA(0,q)或hB(x,q)⊆hB(0,q)成立.

(ii) ∀x∈X,q∈Ω,若hA(x,q)⊆hA(0,q),可得hA(x,q)⊆hB(0,q)或者hB(x,q)⊆hB(0,q)成立.

(iii) ∀x∈X,q∈Ω,若hB(x,q)⊆hB(0,q),可得hA(x,q)⊆hA(0,q)或者hB(x,q)⊆hA(0,q)成立.

(iv)A∈Ω-HFPI(X)或B∈Ω-HFPI(X).

证(i)假设对∀x,y∈X,q∈Ω,hA(x,q)⊃hA(0,q)和hB(y,q)⊃hB(0,q)成立.则有

hA×B((0,0),q)=hA(0,q)∩hB(0,q)⊂hA(x,q)∩hB(y,q)=hA×B((x,y),q).

产生矛盾.因此(i)成立.

(ii)假设存在x,y∈X,q∈Ω,hA(x,q)⊃hA(0,q)和hB(y,q)⊃hB(0,q)成立.因此

hA×B((0,0),q)=hA(0,q)∩hB(0,q)=hB(0,q).

即

hA×B((0,0),q)=hB(0,q)⊂hA(x,q)∩hB(y,q)=hA×B((x,y),q).

产生矛盾,因此(ii)成立.

(iii)证明同(ii).

(iv)对∀x,y∈X,q∈Ω,由(i)可得hA(x,q)⊆hA(0,q)或hB(x,q)⊆hB(0,q)成立.假设hB(x,q)⊆hB(0,q),由(iii)可得hA(x,q)⊆hA(0,q)或hB(x,q)⊆hA(0,q)成立.如果对∀x∈X,q∈Ω,hB(x,q)⊆hA(0,q),则有

hA×B((0,x),q)=hA(0,q)∩hB(x,q)=hB(x,q).

令(x1,x2),(y1,y2),(z1,z2)∈X×X,q∈Ω,因为A×B∈Ω-HFPI(X×X),有

hA×B((x1,y1),q)⊇hA×B((x1,x2)*(z1,z2))*((y1,y2)*(z1,z2)),q)∩hA×B((y1,y2),q)

=hA×B(((x1*z1)*(y1*z1),(x2*z2)*(y2*z2)),q)∩hA×B((y1,y2),q).

(1)

如果令x1=y1=z1=0,则

hB(x2,q)=hA×B((0,x2),q)

⊇hA×B((0,(x2*z2)*(y2*z2)),q)∩hA×B((0,y2),q)

=hA(0,q)∩hB((x2*z2)*(y2*z2),q)∩hA(0,q)∩hB(y2,q)

=hB((x2*z2)*(y2*z2),q)∩hB(y2,q).

即证B∈Ω-HFPI(X×X).

现在考虑对∀x∈X,q∈Ω,有hA(x,q)⊆hA(0,q)成立.假设对∀x∈X,q∈Ω,有hB(y,q)⊃hA(0,q)成立.则

hB(0,q)⊇hB(y,q)⊃hA(0,q).

因为hA(x,q)⊆hA(0,q),则有hB(0,q)⊃hA(x,q).因此

hA×B((x,0),q)=hA(x,q)∩hB(0,q)=hA(x,q).

在(1)中,令x2=y2=z2=0,则有

hA(x1,q)=hA×B((x1,0),q)

⊇hA×B(((x1*z1)*(y1*z1),0),q)∩hA×B((y1,0),q)

=hA((x1*z1)*(y1*z1),q))∩hB(0,q)∩hA(y1,q)∩hB(0,q)

=hA((x1*z1)*(y1*z1),q)∩hB(y1,q).

即证A∈Ω-HFPI(X×X).

现在给出具体例子说明,如果A×B∈Ω-HFPI(X×X),则A和B不一定是X的Ω犹豫模糊P理想.

例3X是一个BCI代数,且|X|≥2.定义X上的Ω-犹豫模糊集,对∀x∈X,q∈Ω,分别定义

则

hA×B((x,y),q)=hA(x,q)∩hB(y,q)=0.4,

即A×B是常函数,因此A×B∈Ω-HFPI(X×X).现在有A∈Ω-HFPI(X),但是当x≠0时,有

hB(0,q)=0.6<1=hB(x,q),

所以B∉Ω-HFPI(X).

定理17设A∈Ω-HF(X),ξ0是X上的强Ω-犹豫模糊关系.则A∈Ω-HFPI(X)当且仅当ξ0∈Ω-HFPI(X×X).

证假设A∈Ω-HFPI(X),对∀x,y∈X,q∈Ω,有

hξ0((0,0),q)=hA(0,q)∩hA(0,q)⊇hA(x,q)∩hA(y,q)=hξ0((x,y),q).

对∀(x,x′),(y,y′),(z,z′)∈X×X,q∈Ω.有

hξ0((x,x′),q)=hA(x,q)∩hA(x′,q)

⊇[hA((x*z)*(y*z),q)∩hA(y,q)]∩[hA((x′*z′)*(y′*z′),q)∩hA(y′,q)]

=[hA((x*z)*(y*z),q)∩hA((x′*z′)*(y′*z′),q)]∩hA(y,q)∩hA(y′,q)

=hξ0(((x*z)*(y*z),(x′*z′)*(y′*z′)),q)∩hξ0((y,y′),q)

=hξ0((x*z,x′*z′)*(y*z,y′*z′),q)∩hξ0((y,y′),q)

=hξ0((x,x′)*(z,z′))*((y,y′)*(z,z′)),q)∩hξ0((y,y′),q),

因此ξ0∈Ω-HFPI(X×X).

反之,假设ξ0∈Ω-HFPI(X×X),则对∀x∈X,q∈Ω,

hA(0,q)=hξ0((0,0),q)⊇hξ0((x,x),q)=hA(x,q).

对∀(x,x′),(y,y′),(z,z′)∈X×X,q∈Ω.则有

hA(x,q)∩hA(x′,q)=hξ0((x,x′),q)

⊇hξ0((x,x′)*(z,z′))*((y,y′)*(z,z′)),q)∩hξ0((y,y′),q)

=hξ0((x*z,x′*z′)*(y*z,y′*z′),q)∩hξ0((y,y′),q)

=hξ0(((x*z)*(y*z),(x′*z′)*(y′*z′)),q)∩hξ0((y,y′),q)

=[hA((x*z)*(y*z),q)∩hA((x′*z′)*(y′*z′),q)]∩hA(y,q)∩hA(y′,q)
=[hA((x*z)*(y*z),q)∩hA(y,q)]∩[hA((x′*z′)*(y′*z′),q)∩hA(y′,q)].

特别地,如果令x′=y′=z′=0,则

hA(x,q)⊇hA((x*z)*(y*z),q)∩hA(y,q).

因此A∈Ω-HFPI(X).

4 结 论

作为模糊集一个重要的分支,犹豫模糊集对研究BCI代数有非常重要的理论意义. 许多文献在研究了BCI代数理论时,侧重点主要是此代数中的滤子和理想等相关性质.本文在相关概念的基础上研究了BCI代数的Ω-犹豫模糊P理想,讨论了它的一些性质,丰富了BCI代数和犹豫模糊集的理论研究.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.