追求内容与过程的结构化

摘"要：教学《认识多边形》一课时，教师围绕“有几条边就是几边形”这个核心问题结构化设计学习内容，并借助分类、数形结合等数学思想结构化组织学习过程，通过将生活场景数学化、将零散知识统整化和将统整内容纵横化，发展学生的直观想象能力，培养学生的空间观念。

关键词：小学数学；结构化；学习内容；学习过程；《认识多边形》

“认识多边形”是苏教版小学数学二年级上册第二单元的教学内容，是在学生直观认识了长方形、正方形、圆和三角形等常见平面图形的基础上，进一步教学多边形的知识。本课的教学重点是根据“边”来判断多边形的方法，充分感知多边形的特点；教学难点是在画、围、剪、搭等活动中，感受图形的联系和变换。教学时，笔者围绕“有几条边就是几边形”这个核心问题结构化设计学习内容，并借助分类、数形结合等数学思想结构化组织学习过程，发展学生的直观想象能力，培养学生的空间观念。

一、教学过程

（一）将生活场景数学化

师"同学们，我们东台西溪已经被中央电视台报道了！走，一起去欣赏吧！（播放视频）这些美景里还藏着我们熟悉的图形宝宝呢，你能指一指或描一描，再说出它的名称吗？

生"我描出的图形是三角形。

生"我找到了一个长方形。

……

师"你们的数学眼光真棒！

（课件在实物上描出图形。）

［说明：课始，让学生通过欣赏家乡美景，发现生活中处处都有图形；而描出或者指出这些图形，则是从具体实物中抽象出几何图形。这是数学化的初始阶段。］

（二）将零散知识统整化

1.认识四边形

（1）设疑引入

师"（画面定格于其中一个长方形）这个长方形本领可大了，还会变魔术呢。变变变，变成了——

生"正方形。

师"还想变吗？再变！变成各种各样的四边形。（指图1）观察这些图形，你有什么问题要问吗？

生"右边的这两个图形我们不认识，它们的名称是什么呢？

生"我还见到过一些稀奇古怪的图形，也不知道怎么称呼它们。

师"你们的想法特别有价值！这堂课，就让我们走进图形的世界。（板书：认识多边形）

（2）体验“围成”

师"（指图1）仔细观察这几个图形，什么变了？什么没变？

生"这些图形都有4条线，有的图形是方方正正的，有的图形有点歪斜。

生"我数了一下，都有4条边；图形形状变了，边的条数不变。

师"是这样吗？我们一起动手来数一数，验证一下。

（学生展示数边的过程，教师注意引导方法，依次数，体验“围成”。）

师"（小结）像这样有四条边的图形就是四边形。（板书：4、四边形）它们的形状变了，边的条数不变。（板书：变、不变）

（3）动手操作

师"我们认识了四边形，现在大家想自己动手做一个吗？请利用课前准备的材料动手做一个四边形。

（学生选择合适的材料动手制作四边形。学生用不同方法创作的四边形如图2所示。）

师"材料不同，方法和形状不同，为什么它们都是四边形？

生"它们都有4条边，所以都是四边形。

生"因为四边形有4条边，这些图形都有4条边。

师"你们说出了四边形的本质特征，真棒！

（4）联系生活

师"我们身边也藏着许多四边形，找找看！

生"课桌的桌面是四边形的。

生"瓷砖的面也是四边形的。

……

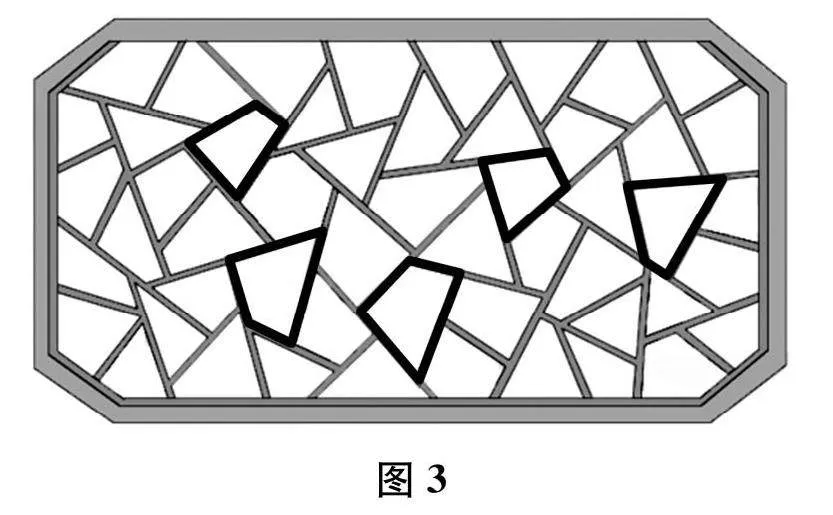
师"（出示窗格图）窗格图案是古代劳动人民智慧的结晶，你能从中找出四边形吗？

（学生找四边形，教师用不同的颜色标注出部分四边形，如图3。）

（5）小结方法

师"我们一起回忆一下刚才研究四边形的方法。先数一数它有几条边，再自己做一个四边形，最后到生活中找一找哪些物体上有四边形。

（板书：数、做、找。）

［说明：学习过程结构化，是学生提升数学学习力的基础。这里，教师先让学生从熟悉的长方形和正方形入手，在“变一变”的过程中，观察、比较多个四边形，排除非本质属性的干扰，找到本质上的联系，抽象出四边形的概念；再回归到数学中，创造多种表征形式的四边形；最后到生活中寻找丰富多样的四边形。这样由特殊到一般再到特殊的认知过程，符合学生的认知规律，让学生的思维不断进阶。同时，变与不变、数形结合的数学思想也在悄然渗透。］

2.认识五边形、六边形

（1）找出图形，描边分类

师"观察窗格图，你看到了什么，能提出一个数学问题吗？

生"我发现窗格图中，除了四边形，还有其他图形，它们是什么图形呢？

师"真是一个爱思考的孩子！

生"我想问的是，窗格图中的每一个图形是不是都有自己的名字？有四边形，是不是还有三边形、五边形？

师"你提的这个问题很有数学的味道！原来，窗格图案里还有其他的图形宝宝，你能用笔描出自己喜欢的图形吗？

（学生汇报，展示在窗格图中描出的三角形、四边形、五边形等。）

师"大家找了这么多图形，看起来有点乱，怎么办呢？

生"按边的条数，从少到多排列。

师"你能想到按照顺序来排列，有序地思考，真棒！

生"可以把边的条数一样多的放在一起，这样就整齐了。

师"（板书：分类）你能进行归类，爱动脑筋的孩子！那请同学们把这些图形分分类吧。

（学生分类，得到图4所示的结果。）

（2）分组研究，交流发现

师"除了我们刚才认识的四边形，剩下的三组，同学们想用什么方法来研究呢？

生"用刚刚研究四边形的方法：数、做、找。

师"研究之前，让我们先来看看活动要求。

（教师出示活动要求：①数一数：它有几条边，给它取个名字；②做一做：你能创造一个同类的图形吗？③找一找：生活中有这样的图形吗？学生小组活动后，交流各自的发现和创造。）

生"我们小组数的是第3组图形，都有5条边，大家给这些图形取的名字是“五边形”。有同学是用笔画了一个五边形，有同学在钉子板上围了一个五边形，有同学发现贴画是五边形的，玩的积木也有五边形。

师"（板书：5、五边形）像这样有5条边的图形是五边形。

（其他小组继续汇报。）

师"（板书：6、六边形）像这样有六条边的图形是六边形。第一组图形，是我们以前认识的三角形，其实也可以叫三边形。（板书：3、三角形）认识了五边形、六边形，你能想到什么呢？

生"如果有7条边就是七边形，如果有8条边就是八边形。

生"七边形就有7条边，八边形就有8条边。

师"同学们在不知不觉中学会了类推。

（3）发现规律，完善结构

师"仔细观察这些图形，你还能发现什么呢？

生"有4条边的就叫四边形，有5条边的就叫五边形，有6条边的就叫六边形。

生"有几条边的图形就是几边形。

师"（板书：几条边、几边形）你的概括能力真强！这些都是我们今天认识的多边形。（同步板贴，最终板书如图5所示）多边形就像一棵大树，它们都是大树结的果实，这也是同学们发现的果实。

［说明：布鲁纳指出：掌握事物的结构，就是使许多别的东西与它有意义地联系起来，进而理解它。简单地说，学习结构就是学习事物是怎样关联的。学生迁移学习四边形的方法，类比认识四边形的过程，自主认识五边形、六边形等。在这个过程中，学生突破了单个知识点的束缚，建立起图形名称与边的关系，发现了“有几条边的图形就是几边形”，把感性经验转化为理性经验，建构了多边形的数学模型。“大道至简”——几条边就是几边形。学生的思维超越了具体图形，而是形成了一种具有一般思想意义的、更为上位的结构性思维。］

（三）将统整内容纵横化

1.横向关联

师"带着你们的收获，和三角形来一次魔幻旅行吧。（课件展示动画）观察大屏幕，三角形摇身一变，变成了几边形？（生答“四边形”）再变成——（生答“五边形”）接下去会是什么图形？（生答“六边形、七边形……”）你发现了什么？

生"每增加一条边就变成了一个新的图形。

师"你们发现了图形之间的联系，真厉害！

2.纵向发展

师"（动画演示正方形依次变成正八边形、正十六边形……）想象一下，如果像这样继续变下去会是什么图形？

生"边会越来越多，变成多边形。

生"我觉得边会变得越来越弯曲，可能会变成圆。

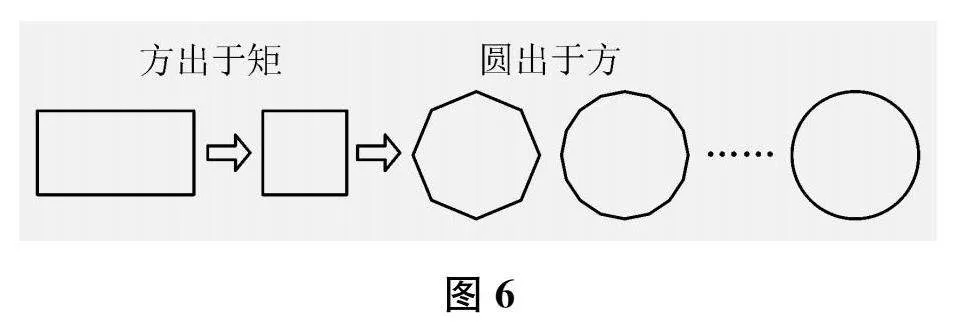
师"很有想象力！我们一起来看电脑的演示。（课件演示正多边形逐渐向圆演变的过程，如下页图6所示）当边无限多的时候，最终就变成了圆。其实，我们的祖先早就发现了这个规律。“圆出于方，方出于矩”，矩是指长方形，也就是长方形可以变成正方形，正方形可以变成圆。数学知识就是这样，横着看，竖着看，之间都是有紧密联系的。

［说明：四边形、五边形、六边形等不是割裂的，是有横向联系的，是可以变换的。学生认识到“每增加一条边就变成了一个新的图形”，多边形是“依靠”边来“命名”的。换一个角度看，正方形变成正八边形、正十六边形……最终变成圆，学生感受到知识是有纵向联系的，具有延展性，并初步体验了转化、极限的数学思想。古语“圆出于方，方出于矩”，寥寥几个字指明了图形的演变和联系，让学生感受到了中国文化的博大精深。］

二、教学反思

教学不是教知识，而是教知识的结构。本堂课，笔者以“多边形本质”为中心，把零散的知识点统整化，纵横交错，形成了一个系统结构，有效促进了学生结构化思维的发展。

（一）结构化搭建学习内容

本课是《平行四边形的初步认识》单元的第一课时，需要引导学生认识多边形，理解“有几条边就是几边形”，整体感知多边形名称的由来。笔者从整体和系统上把握教学内容，不局限于教材中提出的三角形、四边形、五边形、六边形，而是进一步拓宽知识面，延伸到“有几条边的图形就是几边形”。如此，七边形、八边形等多边形的学习就变得“既不费时又不费力”。同时，笔者在知识点的深度和知识之间的贯穿度上做了一定的尝试：在变化中，学生理解了“每增加一条边就变成了一个新的图形”；正多边形在不断增加边的过程中，越来越接近圆。这沟通了多边形之间的联系，构建了正多边形与圆的关联。学生充分感悟，认知的整体性、方法的连贯性、思维的结构性达到了统一。

结构化设计“多边形”学习内容，让知识之间纵横交错，紧密联系，形成一个系统。内容的结构化也促进学生深入理解多边形的共性特征，由浅层学习迈向深度学习。

（二）结构化组织学习过程

波利亚说：教一个概念的时候，应当让学生重走人类思维中的那些关键性步骤。也就是说，学生在获取数学知识的过程中经常采用相同的学习方法，形成科学的方法结构。这堂课，学生通过观察、操作，运用推理、想象和抽象等思维方式，感悟数形结合、分类、极限和转化等数学思想。学习过程的结构化，促进了学生空间观念和几何直观的发展，同时培养了学生的推理意识、应用意识和创新意识。

本课中结构化的学习过程具体体现在以下几个方面。学生从实物图片中描出多边形，用语言描述图形特征，动手操作“创造”多边形，抽象出多边形的外部形象；同时，根据多边形想象生活中的实际物体。通过抽象和想象，从三维到二维，再从二维到三维，发展了空间观念。学生根据图形边的条数进行分类，以边的条数来“命名”多边形，建立形与数的联系，把握多边形的本质，发展了几何直观。从四边形到五边形、六边形，学生归纳、类比，合理地猜想、推理，概括出任何一个（由线段围成的）平面图形“有几条边就是几边形”。在最后的“魔幻之旅”中，学生直观感受到“每增加一条边就变成了一个新的图形”，

发现了图形之间的关系；“圆出于方，方出于矩”，感悟了极限和转化的数学思想。

通过结构化的学习过程，概括了多边形的共性和不同图形的差异，促进知识结构更好地内化为学生的认知结构，成为他们探索新知识、解决新问题的“助推剂”，最终形成嵌入灵魂之中的数学素养。