细分计数单位，凸显运算一致性

摘"要：小数乘法作为基础且关键的数学内容，不仅是学生掌握更高级的数学概念的基石，还对学生数感与运算能力的提升至关重要。教学《小数乘小数》一课时，强调“计数单位”在理解数运算一致性中的核心地位，通过模型图式的实际应用，帮助学生体验0.1与0.1相乘产生新计数单位0.01的全过程，从而深刻领悟小数乘法和整数乘法运算的内在一致性。

关键词：小学数学；计数单位； 运算一致性；《小数乘小数》

小数乘法作为基础且关键的数学内容，不仅是学生掌握更高级的数学概念（如分数运算、代数表达式以及科学计算）的基石，还对学生数感与运算能力的提升至关重要。教学苏教版小学数学五年级上册《小数乘小数》一课时，笔者通过细分计数单位，凸显乘法运算的一致性，提升学生的数学理解能力和运算技能。教学过程及相关思考如下：

一、教学过程

（一）基于实例，感受细分计数单位的起点

（教师出示问题：一台抽水机每小时可以浇地0.1公顷，照这样计算，2小时可以浇地多少公顷？然后，指名学生回答。）

生"0.1×2=0.2（公顷）。

师"这个0.2表示什么意思？

生"0.2表示2小时浇地的面积，因为0.2里面有2个0.1。

（教师出示问题：一台抽水机每小时可以浇地0.1公顷，照这样计算，7小时可以浇地多少公顷？然后，指名学生回答。）

生"0.1×7=0.7（公顷）。

师"0.7表示什么？

生"表示抽水机7小时浇地的面积为0.7公顷，因为0.7里面有7个0.1。

师"这是我们学习过的什么知识？

生"小数乘整数。

师"（出示：一台抽水机每小时可以浇地0.1公顷，照这样计算，0.1小时可以浇地多少公顷？）观察，哪里有变化？请读出来。

生""0.1小时浇地多少公顷。

师"怎样列式？

生"0.1×0.1。

师"这是什么乘法？

生"小数乘小数。

教师从整数乘法入手，逐步引导学生理解计数单位的细分过程。通过复习小数乘整数的实例，学生逐步过渡到小数乘小数的学习中。这既帮助学生巩固了对小数乘整数意义的理解，即计算总共有多少个小数单位，也为学习小数乘小数的算理做了铺垫。

（二）借助面积模型，具象呈现计数单位细分的过程

师"（出示图1）猜一猜，0.1×0.1的得数会比0.1大还是比0.1小？

一台抽水机每小时可以浇地0.1公顷，照这样计算，0.1小时可以浇地多少公顷？

0.1×0.1=？（公顷）

小组合作探究：

1.在图中表示出0.1公顷。

2.分一分、画一画、想一想、写一写，0.1小时可以浇地多少公顷？

生"我觉得结果会比0.1小，因为1×0.1等于0.1，而0.1×0.1中一个0.1和1×0.1中0.1相等，这个因数不变，另一个因数从1变成了0.1，变小了，积也会变小。

师"同意他的想法吗？

生"（齐）同意。

师"0.1×0.1究竟应该等于多少？我们一起来研究。

（学生小组活动，然后汇报交流。）

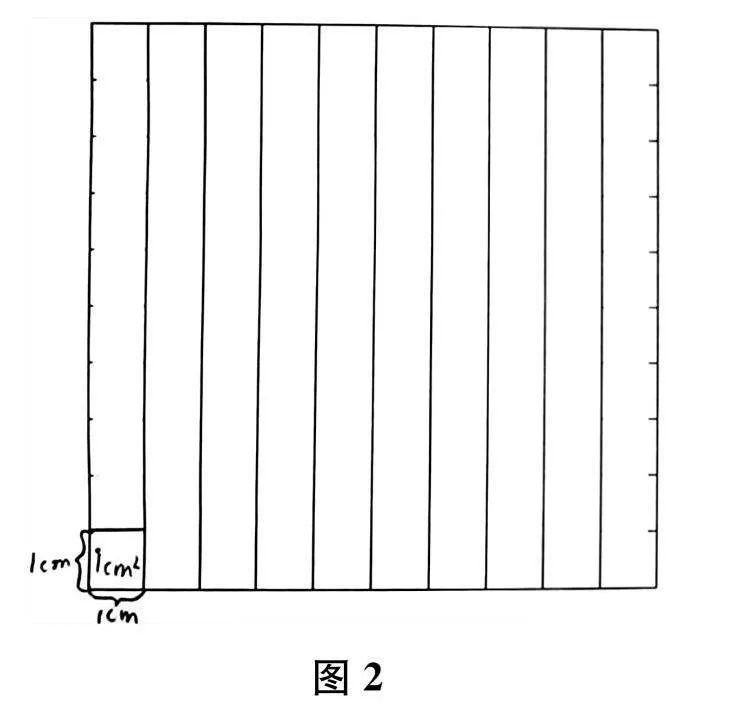
生"（展示探究成果，如图2）我画的这个小正方形表示0.01.因为大正方形表示1公顷，上面的9条竖线把它平均分成了10个长方形，再把每个长方形平均分成10份，10×10是100个格子，这1个格子相当于1公顷的1%，就是0.01公顷。

师"听得懂吗？

生"我有意见。题目的第一个要求是让我们表示0.1，而他直接表示了0.01。（展示探究成果，如图3）我觉得应该像这样先表示出0.1，再把0.1平均分成10份，表示出这样的一份，才是0.01。

生"（展示探究成果，如下页图4）我觉得还应该把格子画满，才能一眼看出表示的是1公顷的1%，也就是0.01。

生"全部画出来更清楚。

师""因此，0.1×0.1=0.01，也就是说，产生了一个新的计数单位“0.01”。

在复习了小数乘整数后，教师调整“计数单位”的应用视角，引入面积模型，帮助学生直观体验因数相乘产生新的计数单位的过程，让学生在操作和讨论中初步感受小数乘法的“理”与“法”一致性。在小组活动中，学生通过画图来表示0.1×0.1的过程，将抽象的数学问题具体化。在汇报交流环节，同伴之间的互动讨论进一步加深了个体对0.1×0.1的理解。通过小组合作，学生能够相互启发，共同探讨问题的解决方法。教师在这一过程中扮演引导者和促进者的角色，鼓励学生大胆表达自己的观点，并对学生的回答作出及时的反馈和点评。

（三）基于计数单位细分的过程，寻找整数乘法与小数乘法的联系

师"现在，我们已经知道0.1×0.1等于0.01，那么其他的小数乘法我们怎样计算呢？

师"（出示：提高效率后，一台抽水机每小时可以浇地0.4公顷，照这样计算，0.3小时可以浇地多少公顷？）请在练习纸上按照刚才的方法想一想，画一画，找一找。

（学生小组活动，然后汇报交流。）

生"（展示探究成果，如图5）0.4=410，所以先把1公顷的正方形平均分成10份，（同步指）0.4在这里。0.3=310，将0.4再平均分成10份，涂出其中的3份。

师"0.3×0.4的结果在图上共有多少个小方格？

生"12个。

师"12表示什么意思？

生"12个0.01，就是0.12。

师"如果没有图，0.4×0.3还可以怎么算？

生"我觉得可以先不看它们的0和小数点，就是4×3=12，最后把小数点点上去。

师"同意吗？可以先算4×3吗？（板书：4×3=12）这个4表示什么？

生"4个110，也是4个0.1。

师"3呢？

生"3个0.1。

师"4个0.1×3个0.1，得到了什么？

生"12个0.01。

师"是的，无论是0.1×0.1=0.01，还是0.3×0.4=0.12，它们都是用0.1×0.1得到了一个新的计数单位。

（出示：一台抽水机每小时可以浇地0.6公顷，照这样计算，0.5小时可以浇地多少公顷？）这道题可以怎样计算？

生"先不看0和小数点，算6×5=30。

师"（板书：6×5=30）6个什么乘5个什么？

生"6个0.1×5个0.1，等于30个0.01。

师""我们回到图中验证一下。（动画演示计算过程）先找到0.6的部分，把0.6再平均分成10份，找到0.5的部分，看一下，是不是30？写的时候写0.30吗？

生"写0.3。

师"这个0.3表示什么？

生"30个0.01，只是写的时候把末尾的0简化了。

师"（出示：①4×3=12，0.3×0.4=0.12；②6×5=30，0.6×0.5=0.30=0.3）比一比每组两道算式，你有什么想说的？

生"计算方法是一样的，都是先算整数乘法，最后点上小数点。

在学生通过面积模型初步理解了小数乘小数的算理之后，教师进一步引导学生抓住计算的关键点，即计数单位的统一，比较整数乘法和小数乘法，发现二者在算法本质上是一致的。

（四）立足数域视角，感悟计数单位的细分与统一

师"（出示：再次提高效率后，一台抽水机每小时可以浇地1.2公顷，照这样计算，3.15小时可以浇地多少公顷？）估一估，3.15×1.2的结果大约是多少？

生"大约是4。

生"大约是3。

生"3—4之间。

生"肯定是一个三位小数。

师"同学们说得都很有道理，自己在本子上列竖式试一试吧。

（学生计算后交流。）

师"（出示图6）请补上小数点，使图中的竖式成为一道小数乘法。

在学生深入理解了小数乘法的意义和过程后，教师可以设计一些跨数域的练习，确保

学生不仅能够熟练掌握计算技巧，而且能够

由此深入理解数的运算本质，拓展完成其他具有挑战性的数学问题。通过这些练习，学生可以发现无论是哪种小数相乘，都可以通过统一的方法来理解和计算：将问题转化为整数乘法，然后根据计数单位的细分程度确定小数点的位置。

二、教学反思

“计数单位”是运算教学的核心概念，学生对其的理解程度直接影响后续学习的效果。因此，在乘法运算的教学中，应突出“计数单位”的核心地位，注重模型图式的应用，多用数理的方式展开算理学习，以帮助学生更好地掌握小数乘法的算法和算理。在本堂课中，教师带领学生经历了0.1与0.1相乘产生新计数单位0.01的全过程，辅以可视化的学习材料，使学生感悟到小数乘法和整数乘法运算的内在一致性。

教学中也存在一些需要改进的地方。其一，教师应加强对学生估算能力的培养。通过估算，学生可以快速判断计算结果的合理性，这对于学生提高计算效率和准确性具有重要意义。在本堂课中，只有计算3.15×1.2时，用到了一次估算。这显然是不够的。其二，教师应注重对学生批判性思维的培养。在讨论小数乘法的过程中，教师可以引导学生深入思考和辩论。比如，教师提问：“为什么小数乘法积的小数位数是两个乘数的小数位数之和？有没有例外的情况？”通过这样的问题，学生不仅能巩固已学知识，还能学会质疑和探究方法，培养问题意识和创新精神。