单元复习教学：以“问题提出”的方式

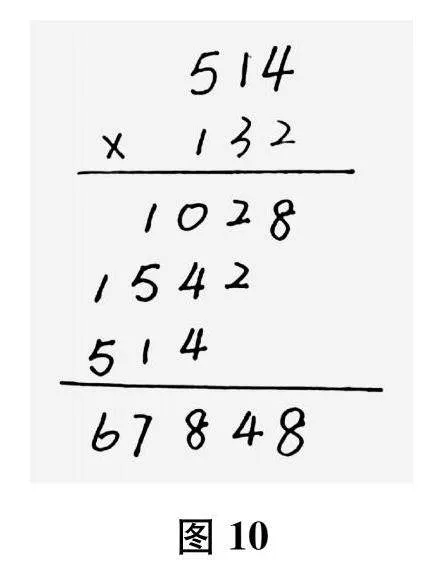
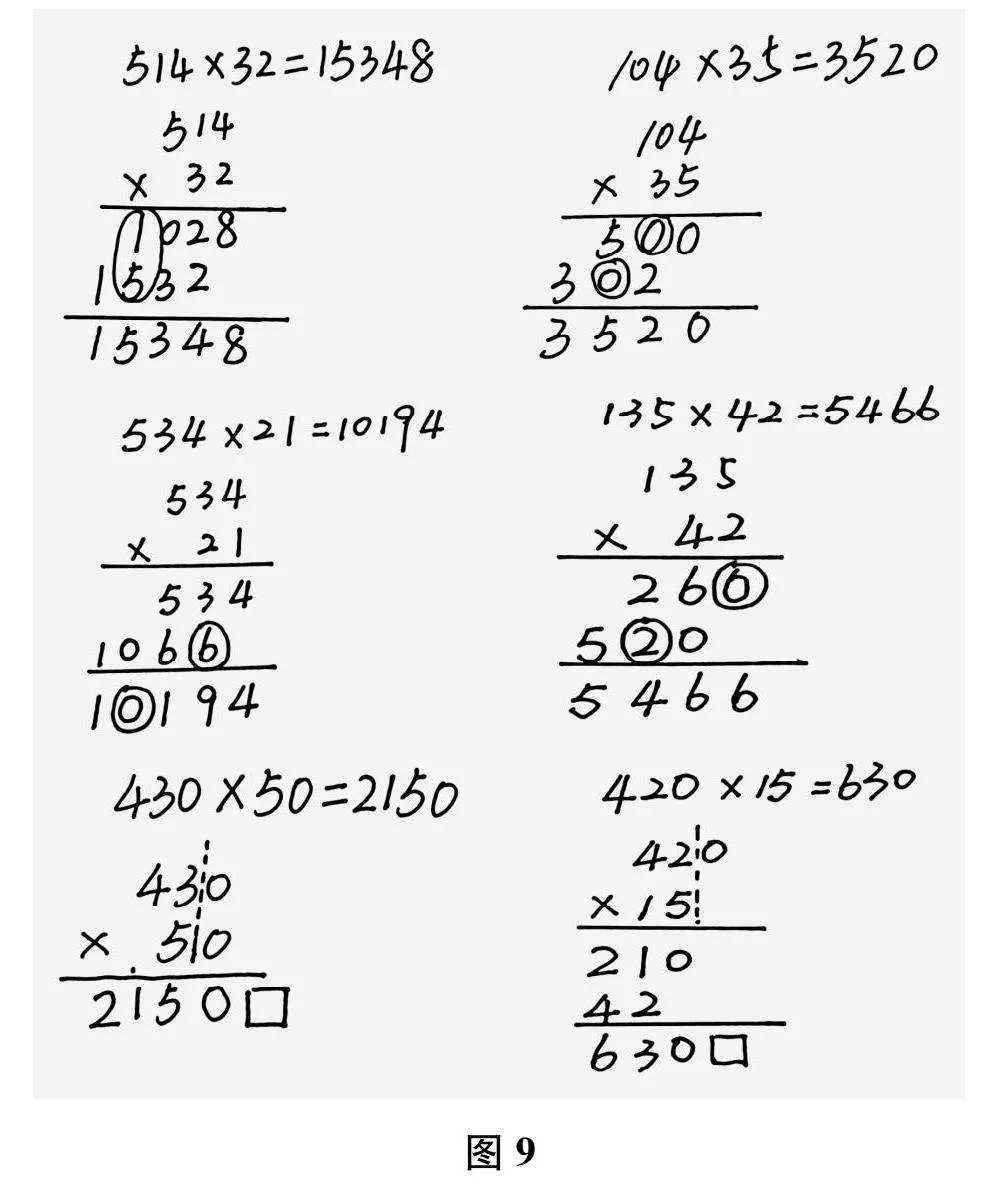
摘"要：《三位数乘两位数》单元复习课，依据“问题提出”的教学理念，设计“选数字组多位数，编写乘法算式”的情境任务，引导学生提出问题，从而激发学习兴趣，丰富学习资源；然后梳理学生编写的乘法算式，帮助学生归类可能的算式，建立模型，归因可能的错误，提醒纠错，并通过拓展算式，迁移运用模型，联系积的变化规律，进一步认识多位数乘法的算理和算法，从而突破计算难点，完善认知体系。这样的教学步骤明确、前后连贯，把原本枯燥、乏味的计算复习课上得更吸引人、更有新意，凸显了“问题提出”教学的优势。

关键词：小学数学；问题提出；三位数乘两位数；模型；纠错

一、教学实践

（一）教前思考

人教版小学数学四年级上册第四单元《三位数乘两位数》包括三位数乘两位数的笔算、积的变化规律、常见数量关系等内容，共有5道例题：例1是三位数乘两位数的一般情况，主要是让学生理解笔算的算理，掌握笔算的算法；例2是因数中间或末尾有“0”的情况，主要是让学生利用“遮零法”转化成学过的两位数乘两位数、三位数乘一位数或两位数乘一位数等乘法来计算；例3让学生观察算式，发现积的变化规律——可拓展到积不变的规律；例4、例5分别是“单价×数量=总价”“速度×时间=路程”这两种常见数量关系的简单应用。本单元是整数乘法的最后一个单元，学生在学习中能否理解算理、掌握算法，对其迁移学会更多位数乘法的计算具有重要的影响。

在新授课的课后作业中，笔者发现，学生计算的兴趣不高，出错率比较高，主要表现为：进位忘记加；数位对错了；对因数末尾有“0”的情况，积后面的“0”忘添或少添了；对因数中间或末尾有“0”的情况，不能区分不同的类型，灵活地运用计算方法……而且，很少能够自主发现错误，更不用说深入分析错因；对算理和算法的认识还不够深刻，不能很好地迁移计算更多位数的乘法。

因此，本单元的复习课，笔者尝试改变传统的教学模式，依据“问题提出”的教学理念，设计“选数字组多位数，编写乘法算式”的情境任务，引导学生提出问题，从而激发学习兴趣，丰富学习资源；然后梳理学生编写的乘法算式，帮助学生归类可能的算式，建立模型，归因可能的错误，提醒纠错，并通过拓展算式，迁移运用模型，联系积的变化规律，进一步认识多位数乘法的算理和算法，从而突破计算难点，完善认知体系；最后关注常见的数量关系，引导学生利用多位数乘法计算的知识解决生活问题。

（二）教学过程

1.设计情境任务，提出计算问题

课件出示数字卡片“0”“1”“2”“3”“4”“5”“0”，提出任务要求：（1）编写一道你能够算对的三位数乘两位数的算式；（2）编写一道你认为其他小朋友容易算错的三位数乘两位数的算式。教师引导学生理解任务要求后，学生根据任务要求编写三位数乘两位数的算式，教师收集学生编写的算式。

［设计意图：设计数字卡片情境，孕伏多位数乘法“数位（计数单位）分解，数字（计数单位的个数）相乘”的算理与算法。分“能够算对”和“容易算错”两个层次让学生编题，激发学习兴趣，丰富学习资源，同时了解学生的“已知”和“不足”，提高教学的针对性。］

2.梳理“能够算对”的算式，归类建模

师"老师从大家那里收集了几道“能够算对”的算式。

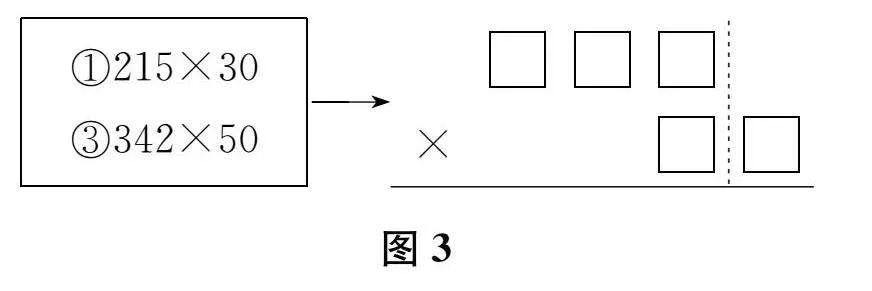
（出示算式：①215×30；②354×21；③342×50；④300×25；⑤530×20；⑥340×21；⑦302×15；⑧250×40；⑨520×43）请看①号算式。让你列竖式计算，你会怎么做呢？

生"（列竖式计算，如图1所示）把30中的“0”遮住不看，把算式转化成215×3，算出积，在后面添上一个“0”，就可以了。

师"很好！（出示图2）老师把这个竖式写成这样的模型，你们能看懂它的意思吗？

生"能。就是刚才的竖式，只是没有把数字填写上去。第二个因数末尾有“0”，可以先算“0”前面的数乘第一个因数的积，再在积的末尾添上一个“0”。

师"再看其他算式，还有哪些算式也可以用这个竖式模型计算？

生"③号算式。

师"（出示图3）这样就把①号算式和③号算式归为一类了。

师"接着看剩下的算式，你能将它们再归归类，并写出类似的竖式模型吗？想一想分类的理由是什么。小组讨论。

（学生小组讨论。）

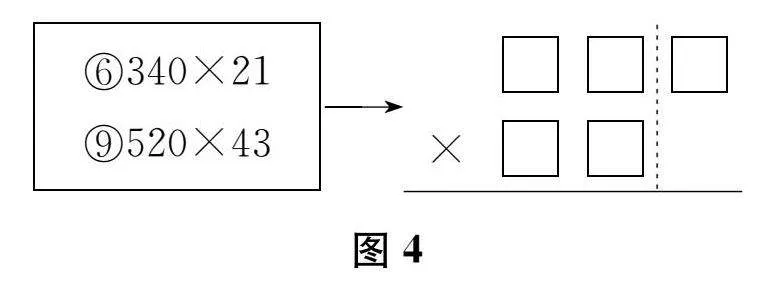
生"我们发现，⑥号算式和⑨号算式是同一类的：第一个因数末尾都有一个“0”。以⑥号算式为例，可以这样算：先把340末尾的“0”遮住，变成34×21计算，再在积的末尾添上一个“0”。（出示图4）可以用这样的竖式模型。

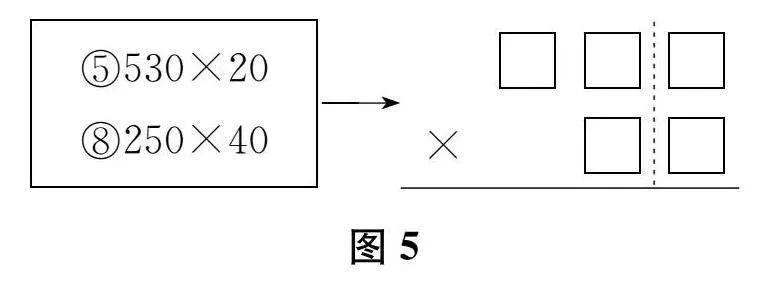
生"我们发现，⑤号算式和⑧号算式两个因数末尾都有一个“0”。列竖式时可以这样算：把两个因数末尾的“0”都遮住，变成两位数乘一位的乘法计算，再在积的末尾添上两个“0”。（出示图5）可以用这样的竖式模型。

生"我们发现，②号算式和⑦号算式两个因数末尾都没有“0”。列竖式计算时，数位要对齐，从个位算起。（出示图6）可以用这样的竖式模型。

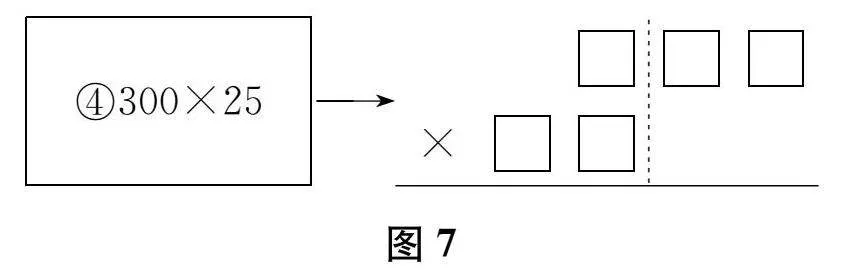
生"我们发现，④号算式第一个因数末尾有两个“0”。先将这个因数末尾的两个“0”都遮住，变成一位数乘两位数的乘法计算，再在积的末尾添上两个“0”。（出示图7）可以用这样的竖式模型。

生"④号算式不用单独分一类。它也是第一个因数末尾有“0”（只不过是有两个“0”）的算式，可以归到⑥号算式和⑨号算式那一类，即第二类；如果交换两个因数的顺序，它就变成第二个因数末尾有“0”的算式，可以归到①号算式和③号算式那一类，即第一类。另外，从将“0”遮住的结果看，它是两位数乘一位数的乘法，也可以归到⑤号算式和⑧号算式那一类，即第三类。

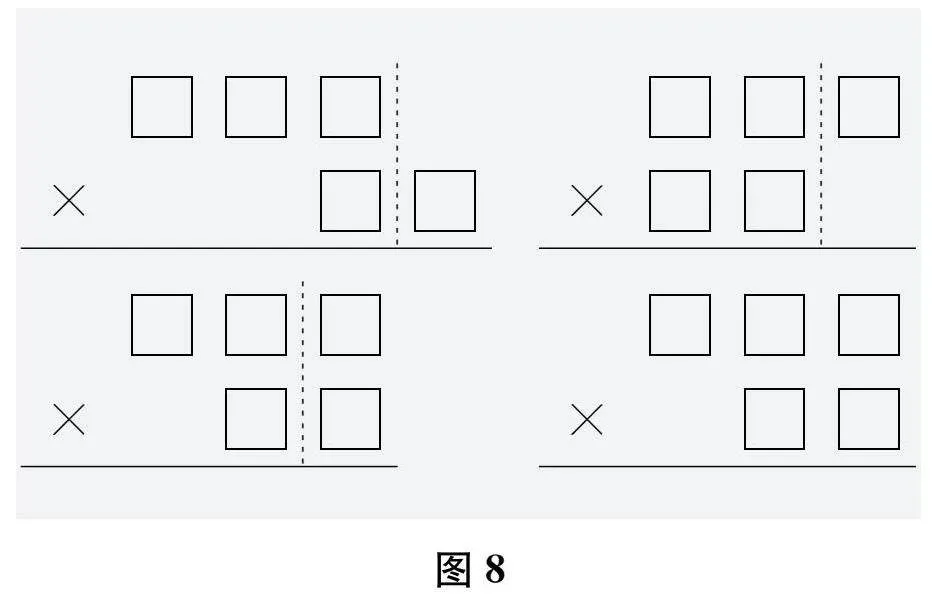
师"讲得真好！模型并不是一个具体的算式，而代表同一类算式。（出示图8）经过同学们的思考、讨论，得到了这四种竖式模型。

［设计意图：在学生“能够算对”的算式中选择丰富的样例，引导学生分类建立三位数乘两位数竖式计算的模型，为进一步认识多位数乘法的算理和算法做铺垫。同时，突出因数末尾有“0”的乘法计算过程中的转化思想，凸显旧知与新知的联系，为完善多位数乘法的认知体系做铺垫。］

3.初步拓展算式，迁移运用模型

师"之前的算式都是三位数乘两位数，都用了5张数字卡片。现在，我们多用一两张卡片，编一些我们还没学过的乘法算式。（出示算式：453×120；3540×21；5410×230）有了这些模型，你会利用它们计算这些算式吗？

生"453×120这个算式，可以用竖式模型一，转化成三位数乘两位数计算，再在积的末尾添上一个“0”。

生"3540×21这个算式，可以用竖式模型二，转化成三位数乘两位数计算，再在积的末尾添上一个“0”。

生"5410×230这个算式，可以用竖式模型三，转化成三位数乘两位数计算，再在积的末尾添上两个“0”。

师"如果在因数的末尾添上更多的“0”呢？

生"还是利用“遮零法”，通过相应的竖式模型计算。

师"同学们真会现学现用！得到了模型，也学会了运用。现在，请大家想一想：“遮零法”运用的是我们学过的哪个知识点？

生"积的变化规律：一个因数不变，另一个因数乘几或除以几（0除外），积也乘或除以相同的数。

生"积的变化规律有一种难一点的情况，是两个因数都变化的情况。这时，积也要相同地变化两次。

师"原来积的变化规律这么有用！同学们不仅要知其然，而且要知其所以然。

［设计意图：多用卡片，将三位数乘两位数拓展为更多位数的乘法，并针对学生计算的难点，聚焦因数末尾有“0”的情况（只有五张非“0”卡片的情境设计使这种情况的出现更为自然），让学生迁移运用三位数乘两位数竖式计算的模型，在特殊情况下进一步认识多位数乘法的算理和算法。同时，联系积的变化规律，揭示“遮零法”背后的道理，加强知识之间的联系。］

4.梳理“容易算错”的算式，归因提醒

师"同学们还编出了一些“容易算错”的算式。很多同学编的是两个因数末尾都没有“0”的算式。为什么呢？你们觉得会错在哪里？

生"因为数字多，进位多，容易把进位忘加或把进位加错。

师"也有同学编的是因数末尾有“0”的算式。这种算式会错在哪里？

生"忘添或少添积后面的“0”。

师"很有道理！请同学们把你编出的“容易算错”的算式用竖式计算，并且把你觉得其他同学会错的地方用红笔标注出来。

（学生计算、标注。教师巡视。）

师"老师从大家那里收集了一些具有代表性的易错题。

（出示图9）从编写第一个算式的同学开始说一说。

生"这个竖式在分步算乘法时都是对的，但是，在算两积之和时把1＋5算成了1×5。我想提醒大家：在计算时，要清楚哪些步骤用乘法计算，哪些步骤用加法计算。

生"先算5×4=20时，应该写0进2；再算5×0=0时，直接写0了，没有加进上来的2。同样地，先算3×4=12时，应该写2进1；再算3×0=0时，直接写0了，没有加进上来的1。我想提醒同学们：在计算时，向前一位进的数可以写在旁边，提醒自己，这样不容易遗忘。

生"乘法口诀记错了，2×4算成6了。另外，算5+6=11时，应该进位，而没有进位。我想提醒大家：在计算时，口诀一定要熟练，并且不要忘记进位。

生"书写潦草，把0写得像6，自己把自己给坑了。另外，算4×5=20时，应该进2，而没有进2。我想提醒同学们：在计算时，书写一定要端正，同时也不要忘记进位。

生"这个竖式其实属于上面的竖式模型三。这时，两个因数末尾都有一个“0”，应该在算出的积末尾添上两个“0”，但是，这里只添了一个“0”。我想提醒同学们：在计算时，在因数的末尾遮了几个“0”，在积的末尾就要添上几个“0”；不能觉得反正都是“0”，就用一个“0”代替多个“0”。

生"我的题目比较特别。420×15用“遮零法”，先转化成42×15=630；这个积末尾本身就有一个“0”，导致忘了在它后面添上之前遮去的“0”。我想提醒大家：计算时一定要小心、仔细，不能跳步骤；特别是，算出的积末尾本身带有的“0”，不要和因为之前遮去因数末尾的“0”而要补上的“0”混淆。

师"很好！这些就是我们平时计算中最容易出错的地方。同学们要注意：计算时，不要混淆加和乘，不要忘加或加错进位，不要忘添或少添“0”，也不能记错口诀，不能书写潦草，而要按照规范的格式和步骤，细心地计算。

［设计意图：在学生“容易算错”的算式中选择丰富的样例，引导学生呈现错误，分析错因，提醒纠错，从而突破难点。这里，学生的生成与教师的预设有一定的差异：学生关注了教师没预设到（不太关注）的“混淆加和乘”“记错口诀”“书写潦草”错误，忽视了教师预设到（较关注）的“数位对错”错误。这也是“问题提出”教学因为学生主体性强而产生的魅力和带来的困难。］

5.进一步拓展算式，打通算理和算法

师"之前，我们在有“0”的情况下，多用了一两张卡片。现在，我们把两个“0”变成一个“1”和一个“2”，依然多用一两张卡片，编一些我们还没学过的乘法算式。（出示算式：514×132；2514×32）你能用竖式计算吗？先算第一个式子。

（学生尝试计算。）

师"谁来说说计算的过程，特别是第二个因数百位上的数应该怎样计算？

生"（列竖式计算，如图10所示）先算第二因数个位上的数乘第一个因数每一位上的数，2×514=1028，积末尾的“8”要和个位对齐；再算十位上的数乘第一个因数每一位上的数，3×514=1542，表示1542个十，积末尾的“2”要和十位对齐；然后算百位上的数乘第一个因数每一位上的数，1×514=514，表示514个百，积末尾的“4”要和百位对齐；最后把这三个积相加。

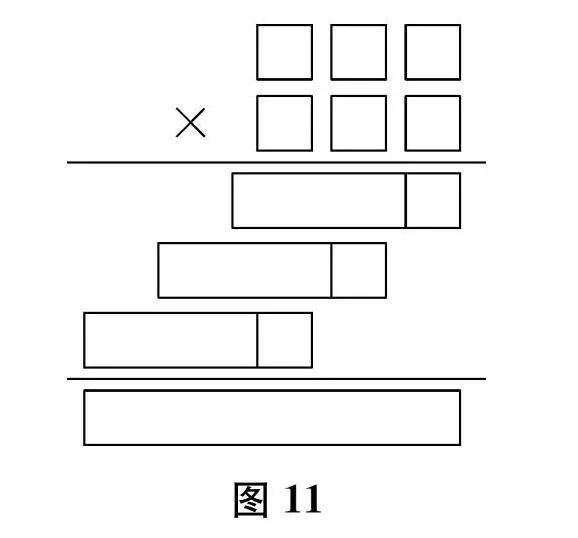
师"讲得非常完整！（出示图11）老师把这个竖式写成这样的模型，你们能看懂吗？

生"看得懂。它表示因数末尾没有“0”的三位数乘三位数的竖式计算。第二个因数个位上的数与第一个因数相乘，得到“几个一”，积的末尾与个位对齐，写在第一行；十位上的数与第一个因数相乘，得到“几个十”，积的末尾与十位对齐，写在第二行；百位上的数与第一个因数相乘，得到“几个百”，积的末尾与百位对齐，写在第三行；再把这三个积相加。

师"这个竖式和我们本单元学习的因数末尾没有“0”的三位数乘两位数的竖式有什么相同点和不同点？

生"计算方法是一样的，只不过多乘了一次。

生"原理是一样的：一位一位分开乘，乘得积再相加，而且每次乘得的积都要注意末尾与第二个因数中相应的数对齐。只是乘的次数不同。

师"同学们观察得很仔细！如果是四位数乘四位数呢？竖式会是怎样的？

生"和刚才的竖式模型一样：只要一位一位地乘，每一位乘得的积末尾与这一位对齐，就可以了。四位数乘四位数，要乘四次，得到四个积，写成四层，再将四个积相加。

生"不管第二个因数有几位，只要每一次乘得的积末尾不对错位，就行了。

师"是的。数学表面上看起来千变万化，实际上“万变不离其宗”。学会了计算原理和方法，多位数乘多位数也就能计算了。第二个式子留给同学们课后计算。

［设计意图：突破难点之后，继续多用卡片，将三位数乘两位数拓展为更多位数的乘法，并从特殊走向一般，聚焦因数末尾没有“0”的情况（需要将两张“0”卡片变为非“0”卡片），让学生迁移运用三位数乘两位数竖式计算的模型，在一般情况下进一步打通多位数乘法的算理和算法，从而完善多位数乘法的认知体系。同时，抓住这一契机，强调了“数位对齐”这一易错之处，补上了教学的漏洞。］

6.关注数量关系，解决生活问题

教师出示如下生活问题，引导学生运用所学的计算知识来解决。

1.估一估，三位数乘两位数的积最大是几位数，最小是几位数？

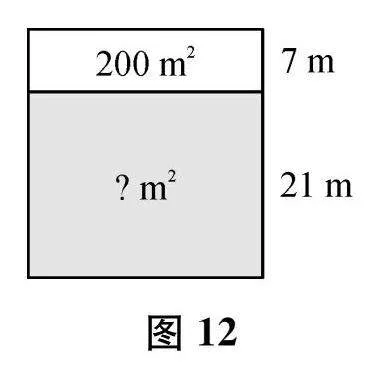
2.如图12，已知白色长方形的面积是200平方米，那么阴影部分长方形的面积是多少平方米？

3.某商场以每个88元的价格购进135个足球，以每个120元的价格卖出，这些足球全部被卖出，该商场一共赚了多少元？

4.一辆货车从甲地开往乙地送货，去时以40千米/小时的速度行驶，3小时正好到达，按原路返回时只用了2小时，这辆货车往返的平均速度是多少？

5.请你选择这节课编写的一道三位数乘两位数的算式，编写一个可以用这个乘法算式解决的生活问题。

［设计意图：计算的重要目的是解决生活问题。因此，课尾关注常见的数量关系，设计生活问题让学生解决。第1题让学生估算：估算是解决生活问题的重要方法。第2题让学生灵活运用积的变化规律解决问题：此题无法利用学生学过的知识直接计算。第3、第4题是常见数量关系的简单应用，让学生体验计算的现实意义。第5题让学生逆向思考，根据算式编写生活问题，帮学生感悟数量关系作为数学模型的应用价值，培养发散思维。］

二、教学评析

这是一堂有关“三位数乘两位数”的复习课，教学的重点是：帮助学生纠正常见错误，突破计算难点；打通算理算法，完善认知体系。

复习课常见的教学方式是：教师引导学生回顾已学知识，建立知识体系后，呈现不同的练习题，让学生去解答。这样的教学常常使学生被动学习，效率不高。 而“问题提出”教学能够给学生更多的自主学习空间，让学生既是问题提出者，也是问题解决者，从而不仅可以激发学生的学习兴趣，而且可以提升学生的思维能力。当然，这样的教学具有更大的不确定性，对教师理解数学、理解学生以及把控课堂的能力提出了更高的要求。

“问题提出”的教学过程往往包括四个基本步骤：呈现问题情境，提出任务要求，学生提出问题，师生处理问题。如何让四个步骤环环相扣，让学生在主动的数学探索中有效地实现教学目标，这是“问题提出”教学的关键所在。本堂课在这方面给予我们很多有益的启示。

本堂课中，“问题提出”的情境是“0”“1”“2”“3”“4”“5”“0”七张数字卡片。因为直接的教学目标是多位数乘法的细节，多位数乘法的原理是基于位值（数位和数字）制记数法的，所以，用相对抽象的可以排列组合的数字作为问题情境，所提的问题比较容易直接和教学目标建立连接。而给出两个“0”，为学生提出特殊情况和容易产生错误的问题提供了丰富的背景材料。

学生提出的问题不仅受问题情境的影响，而且直接受教师引导语（任务要求）的影响。本堂课中，教师用了两句不同的引导语，要求每个学生提出两个问题。第一句引导语要求的“问题提出”比较宽泛也相对容易，可以作为热身活动。和教学目标更为关联的是第二句引导语。这句引导语要求学生提出更难的问题，实质上是鼓励学生把问题情境中的两个“0”合理地用在所提的问题中。这体现了问题情境和引导语的内在联系，而这样的内在联系能让“问题提出”教学更好地服务于教学目标的实现。更有意思的是，在第二句引导语中，教师要求学生提出“你认为其他小朋友容易算错”的题目。这样的要求能帮助那些学习困难的学生提出有效的数学问题。因为有些学生即使不是一个很好的问题解决者，仍然可以提出好问题“让其他小朋友容易算错”。为传统课堂中学习困难的学生提供积极参与的机会，正是“问题提出”教学的一大优势。

当学生提出问题后，“问题提出”教学就进入另一个重要的步骤：师生处理问题。本堂课中，教师没有直接让学生解决问题（进行计算），而用了一个特殊又关键的方法来梳理学生提出的问题：归类建模。图8中师生一起总结出的四种竖式模型，直接体现了两位数乘三位的特殊与非特殊情况。到此，教学目标已经自然地呈现在学生提出的问题中了。显然，要有这样的效果，学生必须提出有效的数学问题。而学生提出有效的数学问题，又和前面教师设置合理的问题情境和引导语密不可分。由于这个环节对数学思维的要求很高，教师合理地运用了小组讨论和全班汇报的方式来完成。通过分类建模完成问题梳理后，就进入问题解决的过程。不难看出，有了“问题提出”的过程，学生无论是对题目的理解还是对题目的感情都不同一般。

值得一提的是，本堂课中，完成了“问题提出”的教学过程后，教师还不失时机地引导学生将所学的知识运用到生活情境中，从而进一步巩固和深化本单元的教学目标。

总之，这堂课的教学步骤明确、前后连贯，把原本枯燥、乏味的计算复习课上得更吸引人、更有新意，凸显了“问题提出”教学的优势。