核心素养引领下的“初中数学教学之习题设计”
孙程程

摘要:数学教学的习题设计要聚焦几个核心问题——注重习题的变式,一题多解,习题设计要体现数学知识的结构,习题训练中能暴露新知的易错点,善于在习题中渗透数学思想方法.追求精益求精的习题设计能力是值得持之以恒探索的课题.
关键词:核心素养;习题设计;知识结构化;数学思想
罗增儒老师说过,谁也无法教会所有的题,重要的是通过有限道题的学习,领悟那种可以解决无限道题的数学素养.高昂的时间成本是教学活动难以逾越的障碍,一节课如果内容太多,任务太重,学生很忙,思考力就难以提升.因此,作为教学设计者和执行人的教师,要反复研读教材,在尊重学生认知规律的前提下设计合理可行的习题,体现教学重难点,不让学生做廉价的发现、无畏的探索.教师在习题设计中要恰当地设置障碍,让学生的思维始终处于活跃状态.鉴于此,笔者结合多年初中数学一线教学经验,具体谈谈初中数学教学中“习题设计”的理念.
1 精心设计习题的变式
变式教学具有得天独厚的优势,它不是一味地灌输知识,而是点燃思维的火焰.变式可以引领学生不断面对新的问题,运用所学知识来解决问题,逐步让知识向深处漫溯,形成知识结构的建构,从而促进思维能力的提高.善于变式体现了一个教师的专业功底.好的变式是一节好课的心脏,能让一节课“活”起来,触发学生的思考.各变式之间,要具备并列或递进的关系,要具有层次性,由易到难,层层递进,环环相扣,前一个问题是后一个问题的基础与铺垫,即思维逐层深入,逐步拓展,达到“会一题通一类”的效果.
下面以“勾股定理”中的习题为例进行变式设计.
例 在Rt△ABC中,∠C=90°,若a=3,b=4,求c的长.
变式1 如图1,一棵垂直于地面的树被台风吹倒,在离树顶部5 m处折断,树顶距树底部4 m,则树高为_________m.
分析:已知直角三角形斜边为5,一直角边为4,则另一直角边为3.学生在实际解决中,容易错把3 m作为答案,忘记树高还要再加折断的5 m,正确答案应是8 m.
设计意图:变式1在勾股定理的基础上,用数学的思维来解决实际问题.变式1用勾股定理搭建思维的扶梯,用数学的眼光来看待现实生活中的实际问题,体会数学的价值与意义.
变式2 一直角三角形的两边长分别为3和4,则此直角三角形的第三边长为_________.
分析: 边长4可以作直角边,也可以作斜边.①当4为直角边时,第三边为5;②当4为斜边时,第三边为7.
设计意图: 变式2从实际问题再回归到数学问题,例题及变式1的解决,为变式2做了足够的铺垫,凸显了分类讨论思想,属于暴露易错点的变式.变式1到变式2的过渡,从形象到抽象,关注了知识的内涵和外延,增强了学生对数学思想方法的感悟以及对数学技能的掌握,积累数学活动经验.
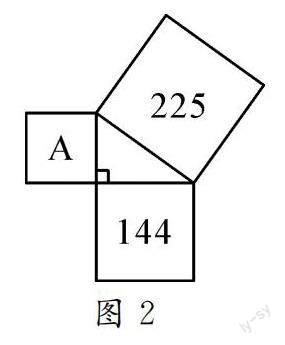
变式3 如图2,三个正方形的边围成一个直角三角形,两个正方形的面积分别为225和144,则正方形A的面积是_________.
設计意图:把勾股定理融入变式中,从数到形,数形结合,让学生在最近发展区引发思考,促进思维的进阶,深度参与解决问题.
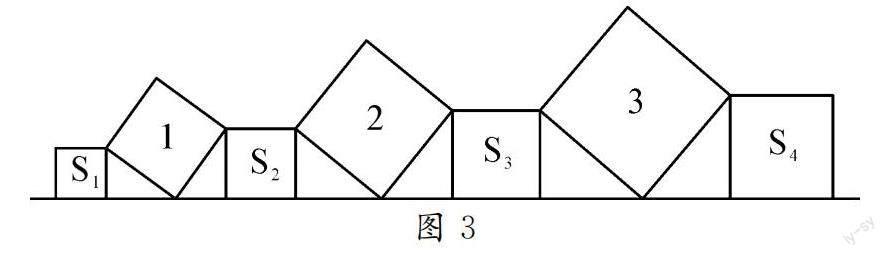
变式4 如图3,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别是1,2,3,正放置的四个的正方形的面积依次是S1,S2,S3,S4,则S1+S2+S3+S4=_________.
设计意图:变式4属于拓展型变式,熟练方能收获巧思,通过变式,增加重复的价值,比投身题海战术收效更大.认知结构上的同化与顺应,促进新图式构建与元认知能力的发展,充分挖掘思维潜能,发展思维的灵活性与深刻性.
变式5 如图4是一个三级台阶,它的每一级的长、宽和高分别为20 dm,3 dm,2 dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是多少?
设计意图:台阶中的最值问题,让学生感悟解决现实问题要关注数学知识背景,在建立模型的过程中学会用数学的思维思考现实世界,有效拓展,深刻理解模型的关键条件,强化数学建模意识,把复杂问题化归为简单熟悉的问题,将知识纵向迁移,提高解题能力.
变式是巩固新知识的好方法,运用变式教学,层层递进,逐步深挖,突破思维定式,激起学生好奇心.通过一系列的变式教学,始终围绕“勾股定理”这个知识“点”,通过变式串成一条“线”,再拓展延伸成“面”.将所学知识融会贯通,在润物无声中培养学生的探知能力,实现从理解知识到掌握知识的飞跃,提升并发展学生数学核心素养.
2 善于设计一题多解的习题
培养思维不设限,一题多解,多方面多角度思考,可以拓宽思路,优化学生的思维品质,提升思维的广阔性、深刻性、灵活性、批判性、独创性;知道为什么这样做,还可以怎么做.学生思维一旦激活,奇思妙想就会宛如“千树万树梨花开”,既巩固了技能,又培养了能力,比再练一道同类题目收益更大.
如:若x=2是一元二次方程x2+4x-p=0的一个根,求该方程的另一个根.
解法一:把 x=2代入方程x2+4x-p=0,得4+8-p=0,解得p=12.
把p=12代入方程x2+4x-p=0,得x2+4x-12=0,解得x1=2,或x2=-6.
所以方程的另一个根为-6.
解法二:设方程的一个根x1=2,另一个根为x2,由根与系数关系,得2+x2=-4,解得x2=-6.
本题以一元二次方程为载体,通过一题多解,让学生感受到应用根与系数的关系解题的优越性,体现发展为本的理念,让学生从“惑”中走出来,知识、素养、经验、智慧都拾级而上.
3 设计体现知识结构、串联新旧知识点的习题
《义务教育数学课程标准(2022年版)》课程实施中提出的教学建议为整体把握教学内容,注重教学内容的结构化.
如,人教版“23.2.3关于原点对称的点的坐标”的教学中,当学生探索并掌握了“平面内的两个点关于原点对称,横、纵坐标互为相反数”这一规律时,笔者设计如下习题.
如:已知二次函数y=ax2+4ax+4a-1的图象是C1,求C1关于原点(0,0)成中心对称的图象C2的函数解析式.
解析:二次函数的解析式可以化为y=a(x+2)2-1,
所以其顶点坐标为(-2,-1).
于是与C1关于原点(0,0)成中心对称的图象C2的顶点坐标为(2,1),且开口与C1相反.
故C2的解析式为y=-a(x-2)2+1.
拓展 二次函数y=a(x-h)2+k(a≠0)关于原点中心对称的抛物线C2的解析式是什么?你发现了什么规律?
解析:二次函数y=a(x-h)2+k关于原点成中心对称的图象开口与原图象相反,顶点坐标是原顶点坐标(h,k)的相反数,即(-h,-k).
所以C2解析式为y=-a(x+h)2-k.
延伸 二次函数y=a(x-h)2+k(a≠0)关于x轴对称的抛物线C2的解析式是什么?你又发现了什么规律?
解析:二次函数y=a(x-h)2+k关于x轴对称的图象开口与原图象相反,頂点坐标与原顶点坐标(h,k)关于x轴对称,即(h,-k).
所以C2的解析式为y=-a(x-h)2-k.
归纳:关于某点成中心对称即是把一个图形绕着某一点旋转180°,其特征为无论作何种变换,抛物线的形状一定不会发生变化,因此|a |永远不变.求变换后的抛物线的解析式时,可以先确定原抛物线的顶点坐标及开口方向,再确定变换后抛物线的顶点坐标及开口方向,然后再写出其变换后抛物线的一般表达式.
设计意图:把坐标平面内“点”的中心对称迁移到“抛物线”的中心对称或轴对称,综合应用了中心对称、轴对称和二次函数的联系,提高学生的知识迁移能力.因此,习题设计的“结构化”体现了课时内容的叠加,把碎片化的知识点有机整合起来,把不同章节的新旧知识点串联起来,由新知联想旧知,通过对比、分析、推理,深入理解知识的内涵和外延,丰富知识网络,完善知识体系,形成高效教学,提升并发展数学核心素养.
4 善于在习题中渗透数学思想方法
以“转化思想”为例:如图5,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点(且点P不与点B,C重合),PE⊥AB于点E,PF⊥AC于点F,则EF的最小值为().
A.4 B.4.8 C.5.2 D.6
本题立足于“垂线段最短”这一知识“生长点”,由已知条件可得四边形AEPF为矩形,锁定已知,构建联系;利用矩形对角线相等的性质,把线段EF的长转化为AP的长;再根据垂线段最短原理,利用等积法即可求解.此过程中让学生积极参与探索,了解问题的实质,产生新旧知识冲突,感受数学发现与创造的快乐,真正做到“懂”“通”“透”,培养学生数学抽象与逻辑推理能力,对数学素养的提升起到“春风化雨,润物无声”的效果.
数学教学的习题设计能力是每一个教师需要终身修炼的教学基本功.它需要教师深入研读教材,重视教材内容的解读,聚焦核心素养,把要传授的内容浓缩体现在习题之中,并将其加工渗透于习题之中,而这又是专业基本功的体现.因此,在教师生涯中,追求精益求精的习题设计能力是值得持之以恒探索的课题.

