“问题串”在初中数学复习教学中的应用探究
孙俏
摘要:问题是数学的心脏,问题的存在让数学学科充满了生机与活力.本文中从理论基础出发,以“一次函数的图象与性质”为例,从精心备课、活动探索与归纳总结三个方面具体阐述如何将“问题串”应用在复习教学中,以提高复习实效,发展学生的数学核心素养.
关键词:问题串;复习;教学
《义务教育数学课程标准(2022年版)》要求学生学会从数学的角度发现问题、提出问题、分析问题与解决问题,以提高知识的应用意识[1].这句话明确了“问题”在数学教学中的重要性.“”问题串”以其得天独厚的优势成为当今数学课堂教学的重要引导模式,研究发现,将“问题串”灵活应用于复习课中,能有效助推学生的思维,提高复习实效.
1 理论基础
1.1 最近发展区理论
维果斯基提出人的认知发展存在“现有水平”与“潜在水平”,介于这两种发展水平之间的为最近发展区.作为教育工作者,关注学生的最近发展区尤其重要.因为低于这个发展区间的教学难度,无法调动学生的学习兴趣;而高于这个区间的教学难度,又会削减学生的学习信心.因此,结合学情,设置处于学生最近发展区内的问题,才会有效激发学生的探索欲.
值得注意的是学生的最近发展区是动态变化的,因此问题的设计也应随之改变.“问题串”的设计一般遵循由浅入深的顺序,从学生的最近发展区出发,带领学生逐层深入地发展思维,提高认知水平,使得问题与学生的最近发展区始终处于对应水平.
1.2 建构主义理论
皮亚杰在《发生认知论》中提出:学生总是从自身的认知结构出发汲取知识,而认知结构一直在不断地更新,这就导致不同阶段的认知图式出现了差异[2].因此,需帮助学生建立知识间的联系,为建构完整的知识体系奠定基础.建构主义理论着重强调学习观、学生观、知识观与教学观对教学的影响.
“问题串”的解决,师生、生生之间积极的互动与交流对帮助学生更好地获得知识间的联系具有重要价值.基于建构主义理论基础,将“问题串”应用于数学复习课中,学生以已有的知识结构为基础,成为知识的主动建构者,并在阶梯状“问题串”的引领下重组知识结构,完善知识体系.
1.3 布鲁姆-特内教学提问模式
布鲁姆-特内教学提问模式将提问分为“知识、理解、运用、分析、综合、评价”六个水平,这六种水平由浅入深地呈现出问题的“点—线—面—体”[3].学生在追求思维的高阶发展时,可结合布鲁姆-特内教学提问模式设计“问题串”.如此设计出的问题层次清晰、条理分明,学生的思维可随着问题的变化呈螺旋式上升趋势.
2 例談实施措施
2.1 精心备课——结合学情制定目标
复习教学的目的是为了巩固、提升学生原有的知识结构,对存在的问题进行查漏补缺.那么,教师在课前需精心研究学情,探寻学生的易错点,结合学生认知漏洞设计教学目标,择取典型例题进行复习教学,让学生在教学过程中自主发现并解决问题,为形成完整的知识结构奠定基础.
一次函数的图象与性质难度不大,大部分学生在新课授课时掌握得较好,但在实际应用上仍不够灵活.因此,在设计复习课教学时,笔者以学生喜闻乐见的活动课方式进行授课,让学生在由浅入深的“问题串”的引领下逐步提高知识的应用能力.
2.2 活动探索——逐层深入发展思维
活动1:知识点的回顾.
问题1 已知一个等腰三角形的周长为4,腰长为x,底边长为y,该三角形的底边长是腰长的函数吗?说明理由.
追问1:写出这个函数表达式.
追问2:这个问题中的自变量的取值范围是什么?
追问3:若去掉“等腰三角形”这个背景条件,该函数自变量的取值范围是什么?
追问4:观察该函数表达式,这是一个什么函数?
教师择取学生通过独立思考获得的各个问题的答案进行投影.生生之间互相纠错,表述解决问题的关键点.教师将本题所涉及到的知识点进行板书.
设计意图:以等腰三角形三边关系唤醒学生对一次函数的回忆,而三角形两边之和大于第三边又为解题增加了隐含条件.设计本题意在培养学生的逻辑思维能力与解题技巧,涉及到的知识点有函数的定义、表达方法、自变量的取值范围以及一次函数的定义等.
活动2:一次函数的图象与性质.
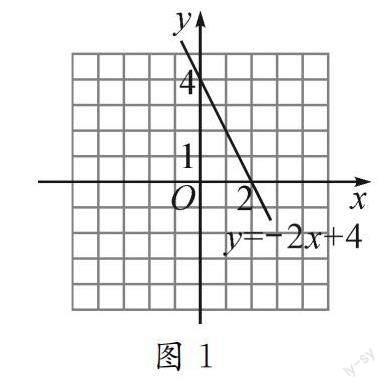
问题2 将问题1中的一次函数图象画在平面直角坐标系中(如图1),观察图象,你有什么发现?
追问1:一次函数图象是怎么画出来的?
追问2:通过这个函数图象,能解决哪些问题?
如,y=0,x的值是多少?y<0,x的取值范围是什么?y>0,x的取值范围又是什么?
学生独立思考并画图,举手表达自己通过观察所获得的结论.教师引导学生对结论进行补充、完善,课堂氛围达到小高潮.教师将本题涉及到的知识点进行梳理、板书.
设计意图:这是一个开放性问题,不同水平层次的学生所形成的感悟各不相同.引导学生互相补充的过程,实则为发散学生思维、拓宽学生视野的过程,这是激发学生潜能、促进思维发展的重要方式.追问的提出,意在让学生通过数形结合思想,将一次函数和一元一次方程以及一元一次不等式建立关联,并在图象上进行描述.
活动2复习的知识点:①用两点法画一次函数图象;②复习一次函数单调性、平行与平移等内容;③建立一次函数和一元一次方程以及一元一次不等式间的联系.
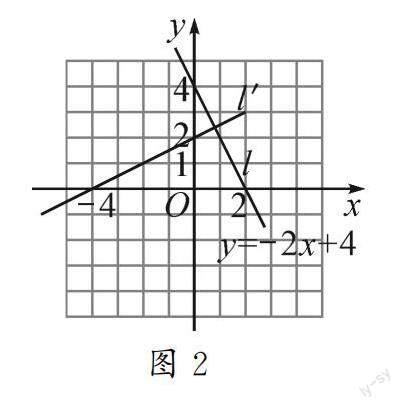
问题3 请在图1的直角坐标系中画出一次函数y=-2x+4的图象l绕原点旋转90°之后的图象l′,并写出l′的函数表达式.(见图2)
追问1:说说你们是怎样画出图象l′的?
此环节,给予学生充足的思考与画图时间,并将学生所画图象进行投影,及时纠正部分学生的错误.通过互动的方式,学生自主表达画图方法.必要时教师进行适当点拨.
设计意图:一次函数图象的旋转问题是复习的重点与难点,这部分内容不仅需从代数角度考虑待定系数法,还需从几何角度思考旋转问题.因此,给予学生充足的时间,进一步深化对基础知识的理解,同时感知数形结合思想的妙处.
问题4 以上问题中,直线l与l′的交点坐标是什么?
追问1:请观察图象,分析当x分别取什么值时,会出现y1>y2,y1=y2,y1<y2的情况?
追问2:当x取什么值时,y1>y2≥-2?
追问3:直线l,l′与x轴所围成的三角形面积是多少?
学生通过独立思考与合作交流自主完成以上所有问题.教师将学生的结论进行投影,让生生之间互相纠错.通过问题的引导,学生完成问题的同时也提炼出比较两个一次函数大小的具体方法,这为提高解题能力奠定了基础.
设计意图:随着课堂的推进,复习内容的难度逐渐加深,问题4的提出意在让学生在掌握基础知识的同时学会应用分类讨论思想解决实际问题.追问3的提出,意在考查学生对知识的综合应用,为后续解决更多综合性问题作铺垫.
2.3 归纳总结——思维导图建构体系
要求学生回顾本节课所学内容,并将各个知识点在草稿纸上罗列出来,并用思维导图将知识与知识之间的联系表达出来,进一步巩固对一次函数图象及其性质的认识.
总之,将“问题串”应用到复习教学中,不仅能进一步巩固与提升学生的“四基与四能”,还能对学生进行学习方法上的指导,帮助学生提炼数学思想方法,促进数学核心素养的形成与发展.
参考文献:
[1]中華人民共和国教育部.义务教育数学课程标准(2022年版)[S].北京:北京师范大学出版社,2022.
[2]皮亚杰,英海尔德.儿童心理学[M].吴福元,译.北京:商务印书馆,1980.
[3]安德森.布鲁姆教育目标分类学(修订版):分类学视野下的学与教及其测评[M].北京:外语教学与研究出版社,2009:69.

