例谈核心素养视域下的教学整体把握

罗尉

摘要：二次函数是初中函数教学主题中的重要内容，需要以大单元视角进行教学整体把握，才能更好地让学生体会到函数教学主题内容的整体性、逻辑的连贯性、方法的普适性、思想的一致性、思维的系统性，积累基本活动经验，形成科学的思维习惯、发展核心素养.

关键词：单元教学；函数主题；二次函数

《义务教育数学课程标准（2022版）》（下简称新课标）在教学建议中特别提出“教学目标的设定要体现整体性”，“改变过于注重以课时为单位的教学设计，推进单元整体教学设计，体现数学知识之间的内在逻辑关系，以及学习内容与核心素养表现的关联”^［1］.基于此，笔者结合“二次函数的图象与性质”教学实际谈谈以单元主题教学来实现教学整体把握的实践与思考.

1 教学分析

1.1 已具备的认知水平和活动经验

在一次函数图象的研究过程中，学生已经体会到“列表—描点—连线”是画任一函数图象的“通性通法”.在反比例函数图象与性质的研究中，学生根据函数表达式的结构联想函数图象的形结构^［1］，再借助通法画出函数图象，从“由数想形”到“由形定性”，体会数学中研究函数图象的基本方法.在数学活动中，通过研究图象的平移，知道在y=k/x+b與y=kx+b中，常数b起到上下平移的作用；在y=k（x+h）与y=k/x＋h中，常数h起到左右平移的作用.这些数学活动经验的积累，可以辅助学生确定二次函数图象的研究思路以及具体的研究方式和方法.

1.2 确定二次函数图象与性质的研究思路

复杂的问题要从最简单的入手，二次函数图象的研究可以从y=ax²开始，对于这类形式的二次函数的图象与性质，可让学生借助已有经验自行研究.接着，大部分学生会自然地去研究y=ax²+k的图象，毕竟已经有了图象上下平移的研究经验.但学生的思路如何能自然地生长到研究y=a（x+h）²的图象上呢？这个时候，学生很容易受一般式y=ax²+bx+c的影响，直接在此基础上加上一次项，从而去研究函数y=ax²+bx或y=ax²+bx+c的图象.这时，不要怕出错，更不要直接要求学生回到预设的研究思路上来.不妨大胆地让学生尝试，在他们发现这样研究比较“麻烦”或者与之前的研究相距甚远时，再引导学生借助经验回头看看，便能发现上下平移研究后，还可以通过左右平移变化来继续研究形如y=a（x+h）²的二次函数的图象，进而研究形如y=a（x+h）²+k的二次函数的图象，思路也就更加顺利、自然.这样学生会对函数图象研究思路的理解更加深刻，以后也可用同样的方法去研究更高次的函数图象.

2 教学片段

2.1 环节一：提出问题，讨论研究方法

问题1 上节课我们从实际问题中抽象出了一类函数——二次函数，它丰富了函数家族，你能写出一些具体的二次函数吗？

追问1：你能将这些二次函数进行分类吗？

追问2：你能表达出每种形式的二次函数吗？

追问3：任意二次函数y＝ax²＋bx＋c都能写成y=a（x+h）²+k的形式吗？

设计意图：学生自己归纳出二次函数常见的几种形式，为后面图象与性质的研究做铺垫.

问题2 如果我们继续研究，你认为可以研究二次函数的哪些方面？你是怎么想到的？

追问1：为什么我们要研究这些内容？

追问2：怎样研究二次函数的图象与性质？

问题3 你打算从哪种形式的二次函数开始研究？为什么？

2.2 环节二：合作学习，研究函数性质

活动一：将学生分成几个学习小组，以小组为单位自主研究二次函数y＝ax²的图象和性质.

设计意图：让学生借助已有的活动经验自主探究，进一步积累研究函数图象与性质的经验和方法，掌握绘制二次函数图象的技巧，体会从特殊到一般解决问题的思维方式.

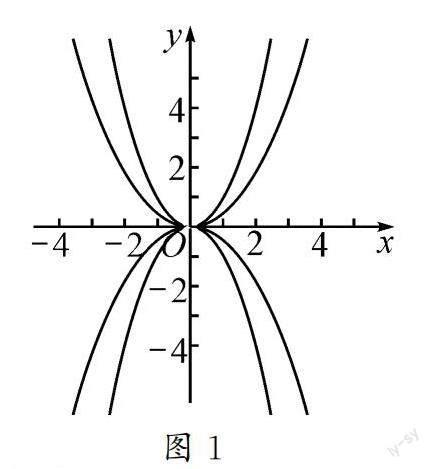
展示不同小组画的函数图象（如图1），让学生意识到a决定二次函数图象的开口方向和大小.再借助“几何画板”动态演示，让学生直观地体会a的变化与图象变化的对应关系.

2.3 环节三：共同讨论，明确研究路线

问题4 接下来，研究哪种形式的二次函数？

追问1：为什么要这样研究？

追问2：我们以前有过类似的研究吗？

追问3：函数图象左右（上下）平移反映到表达式上是如何变化的？你有什么猜想？

追问4：如果这个猜想正确，那么下一步你打算研究图象的什么平移？以前有这样的研究经验吗？

追问5：是否研究了所有的二次函数的图象特征？

设计意图：借助y＝ax²的图象，通过平移，可得出其他形式的二次函数图象，明晰研究二次函数图象的路径（如图2）.让学生体会从特殊到一般解决问题的思想方法，结构化分解问题，感受数学思维的力量，体会探究解决问题策略的魅力，理解研究问题先思后做的重要性^［2］.

活动二：借助研究y=ax²图象的经验，根据讨论的研究路线，自主研究函数y=ax²+k，y=a（x+h）²以及y=a（x+h）²+k的图象与性质.

设计意图：让学生运用平移法画出函数图象，说出函数的大致性质，教师通过“几何画板”进行验证.在此过程中，可以借助“几何画板”的动画演示，帮助学生理解常量h，k对函数图象位置的影响，明确形如y=a（x+h）²+k的二次函数中常量a，h，k的作用.

问题5 你打算如何画y=ax²+bx+c的图象？

设计意图：倒逼学生将一般式y=ax²+bx+c通过配方法转化成y=a（x+h）²+k的形式，借助刚才的研究方法得出其函数图象，让学生感受结构化解决问题的便捷性.当然，还可以采用“列表—描点—连线”这样的通法画函数图象.

若在第一个环节中，学生归纳了二次函数y=a（x+m）（x+n）的形式，这时候可以引导学生先观察函数表达式的结构，借助一元二次方程中因式分解法的学习经验，容易想到点（-m，0）和（-n，0）对应着函数图象与x轴的交点，再借助常量a就可以簡单地画出该二次函数的图象.当然，这里处理的程度取决于学生的研究能力.

3 教学反思

3.1 积累数学活动经验，建构知识体系

教材中函数主题的内容被安排在不同的学期，希望通过螺旋上升的方式帮助学生逐步理解函数.因此，在函数的教学中更需要教师以主题单元等形式进行整体把握，逐步推进.通过整体把握教学内容，教师了解本章知识的产生与来源和发展的结构及其相互之间的关联，以及它们具有的价值和意义，建立对所学知识的本质理解，帮助学生结合已有的认知，建构条理分明、互相关联的数学知识体系.

在积累数学活动经验的过程中，体会和感悟不同数学教学内容背后具有一致性、可迁移性的数学思想与解决问题的方法，学会研究一类问题的方法^［2］.在遇到新问题时，能借助已有的数学活动经验，结构化地分析问题，创造性地解决问题.

3.2 渗透数学思想方法，发展核心素养

数学核心素养的发展具有阶段性、连续性、整合性等特点.教学的整体把握，因其具有整体性的目标设计与规划，所以更有利于学生逐渐形成科学的思维习惯、发展核心素养.函数的教学内容尤其是其中蕴含的数学思想，学生需要在较长的过程中逐步认识与理解.在此过程中，教师可以引导并帮助学生提炼出能打通数学知识之间的关联、发挥核心作用的数学思想方法.

教师在教学中只有关注到教学内容及其相关内容的整体性、逻辑的连贯性、方法的普适性、思想的一致性、思维的系统性^［2］，才能引领学生亲历研究学习内容的一般过程，并在此过程中建构起有效的认知结构，体会不同研究对象之间研究方法的一致性和可迁移性.这样方可帮助学生逐步理解学习内容的本质，学会用整体的、联系的、发展的眼光看问题，用所学的知识和方法解决问题，形成科学的思维习惯，发展数学核心素养.

参考文献：

［1］中华人民共和国教育部.义务教育数学课程标准（2022年版）［S］.北京：北京师范大学出版社，2022.

［1］卜以楼，伍银平.唤醒 传承 延伸——“二次函数的图像”教学分析及思考［J］.中学数学教学参考，2015（20）：12-15.

［2］孙晓天，沈杰.义务教育课程标准（2022年版）课例式解读初中数学［M］.北京：教育科学出版社，2022：124-126.