基于最小二乘离散状态空间的振级计算方法∗

夏遵平， 王 彤， 王 彧， 范新亮

（1.南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016）

（2.江苏环保产业技术研究院股份公司 南京，210036）

引 言

近年来，由交通干扰、机械运转等人为因素产生的环境振动问题尤为突出。以交通干扰为例，轨道交通（高铁、地铁、轻轨等）为人们的出行提供了便捷，但列车运行产生的环境振动将严重干扰轨道线路周围居民的生活，甚至损毁周边敏感建筑［1-2］。因此，环保部门将环境振动问题作为环境综合治理的重要内容，并为此新修订了环境振动的测试与评价准则［3-4］，规定采用人体全身振动评价指标中的计权振动加速度级（简称振级）作为环境振动的评价指标［5-6］。

我国新版人体全身振动评价标准［7］直接引用国际同名标准ISO 2631-1—1997［8］，该标准详细规定了加速度计权的方式和振级的计算方法，要求加速度需按1/3 倍频程进行计权［9］。因此，对测试得到的离散加速度数据按1/3 倍频程的方式进行计权是振级计算过程中的重要步骤［10］。常见的加速度计权方法有频谱方法［11］、百分比带宽滤波法［12-13］等。频谱方法首先估计加速度信号功率谱密度，然后根据Parseval 定理计算每个1/3 倍频程带内的总功率并乘以对应的计权因子。该方法的优点是利用了快速Fourier 变换，计算效率很高，但对于要求以1 s 为积分周期的振级估计，其频率分辨为1 Hz，故无法基于该Fourier 谱对频程带小于1 Hz 的1/3 倍频程进行划分，只能采用近似估计，因而可能引入较大的误差［14］。等百分比带宽滤波法首先根据1/3 倍频程带进行数字滤波，得到每个频程带内的时域数据，然后求其均方根并乘以对应的计权因子。该方法避免了低频带宽无法划分的问题，但需要采用滤波器组对每一频程带进行时域滤波，计算效率较低。此外，文献［7］给出了一种用于拟合计权网络曲线的模拟滤波器，采用该滤波器计权不再直接基于1/3 倍频程的划分，但需要采用合适的方法将其转化为数字滤波器，如文献［10］中采用的双线性变换法。然而，欲使变换后的系统在所关心频带内具有可靠的精度，该方法所需的采样频率要远大于采样定理的要求。在采样时间固定时，较高的采样频率意味着更大的数据样本数，将耗费更多的数据存储和计算开销。

笔者提出一种基于最小二乘-离散状态空间的加速度计权方法。首先，由文献［7］给定的计权参数构建出单输入-单输出（single input single output， 简称SISO）系统的传递函数；然后，采用最小二乘拟合法，将该传递函数转化为离散的SISO 状态空间模型；最后，以原始加速度数据作为系统输入，得到的系统响应即为计权加速度。本方法避免了1/3倍频程的划分和对应频带数据的转换，有效提高了计算效率。通过仿真和实测算例验证了所提方法具有兼顾计算精度和计算效率的优点。

1 理论背景

1.1 计权网络的状态空间形式

文献［7］给出了所关心频带内频率计权传递函数的构造参数。对于Z 振级，采用Wk计权因子组成的计权网络，其由4 种功能传递函数组成，分别为

其中：Hh(s)，Hl(s)，Ht(s)和Hs(s)分别为高通、低通、加速度-速度转换和高阶滤波器的传递函数；s为拉氏变量。

将式（1）~（4）所代表的滤波器级联，得到计权滤波器为

式（5）按系数展开为

联立式（1）~（5），求得Wk计权传递函数的分子与分母系数如表1 所示。

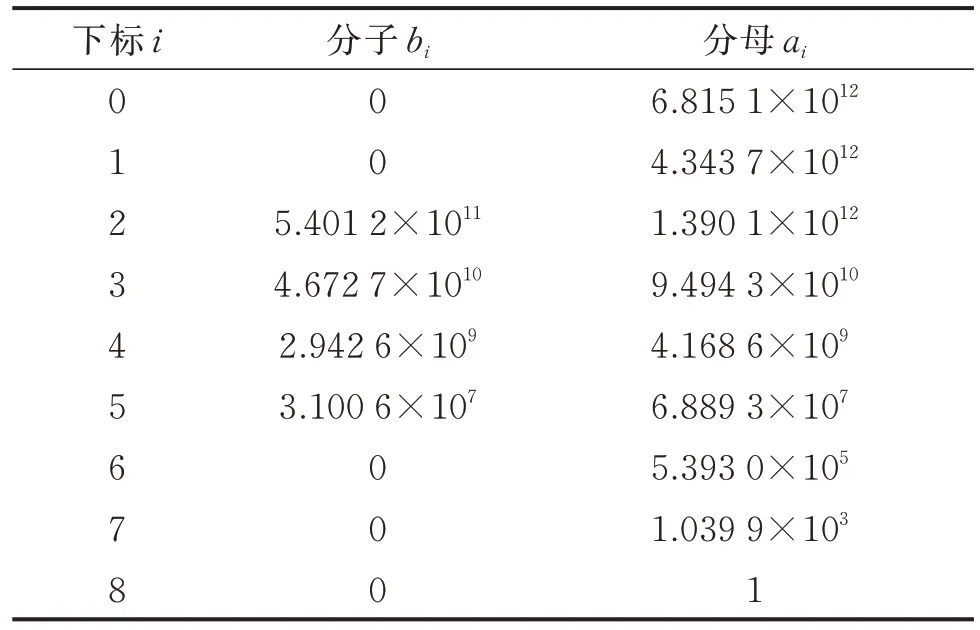
表1 Wk计权传递函数的分子与分母系数Tab.1 The numerator and denominator coefficients of the transfer function of the weightings Wk

将这些系数转化为连续SISO 系统的状态空间，对应的系统矩阵分别为

其中：A∈R8×8为状态矩阵；B∈R8×1为输入矩阵；C∈R1×8为输出矩阵；D∈R1×1为前馈矩阵。

同理，根据Wd计权值亦可求得用于横向（y）和纵向（x）振级计算的状态空间矩阵，其计权传递函数的分子与分母系数如表2 所示。

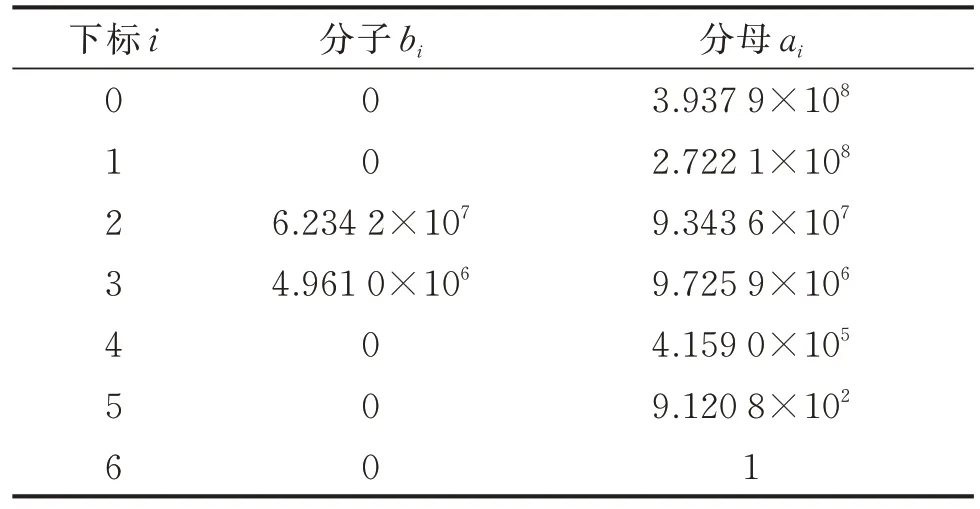
表2 Wd计权传递函数的分子与分母系数Tab.2 The numerator and denominator coefficients of the transfer function of the weightings Wd

上述得到的连续系统不能直接将离散时域数据作为输入，在实际应用中还需将其转换为离散系统。

为实现该转换，采用最小二乘向量拟合法，使连续系统和离散系统的频响函数在关心频带内误差最小。设连续系统频响与离散系统频响之间的误差函数为

进一步得到所有谱线的误差函数为

其中：Nf为谱线数；上标H 表示共轭转置。

要使式（11）取极小值，可由最小二乘得

其中：J为Jacobian 矩阵。

P，L分别为

将式（13）的等式两端同时左乘Jacobian 矩阵的共轭转置，得到正则方程为

其中：R=Re(PHP)；S=Re(PHL)；T=Re(LHL)。

经过简单化简，可得到分子、分母多项式系数，进而得到离散系统的状态空间矩阵Ad，Bd，Cd和Dd，其中Ad为分母多项式系数向量α的伴随矩阵。

1.2 振级估计

得到离散状态空间后，计权加速度可表示为SISO 系统的输出，即

其中：y（k）为系统的状态响应；x(k)为原始加速度；xw(k)为计权后的加速度。

基于计权后的加速度可采用线性平均或指数平均估计加速度的计权运行均方根值，即

其中：N为计算时间周期T内所包含的数据样本数，通常T取1 s。

计算得到瞬时振级值为

其中：a0=10-6m/s2，为基准加速度有效值。

取瞬时振级中的最大值即为最大振级。

2 算例分析

2.1 离散计权系统

当采样频率为400 Hz 时，分别采用双线性变换法［6］和本研究的最小二乘状态空间法计算离散系统，得到1~100 Hz 内Wk和Wd计权因子组成的频响函数，不同方法得到的Wk和Wd计权因子曲线分别如图1，2 所示。图中理论值取自于文献［7］中的1/3 倍频程频率对应的计权因子。结果显示，在400 Hz（等于4fmax）的采样率下，通过双线性变换方法获得的离散系统的频响曲线在频率大于31.5 Hz后呈现明显的偏差，而采用本研究方法获得的频响曲线在整个频带内都与理论值匹配较好。

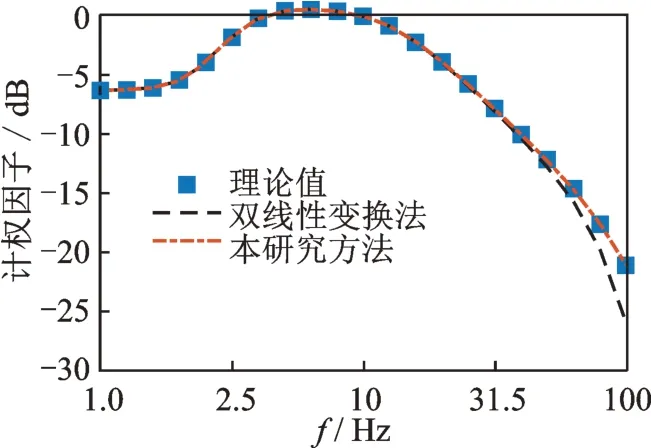
图1 不同方法得到的Wk计权因子曲线Fig.1 Curves of Wk obtained by different methods

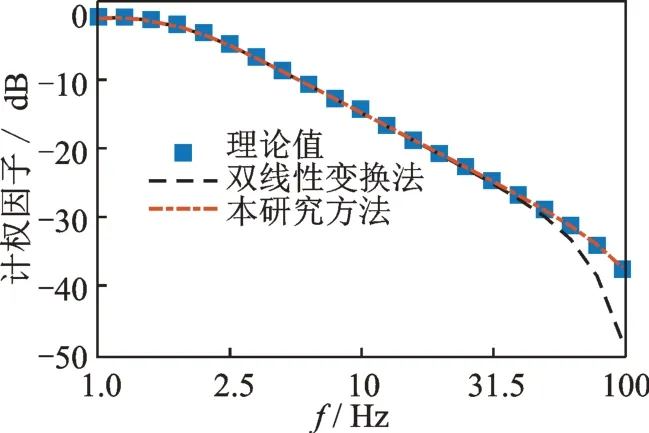
图2 不同方法得到的Wd计权因子曲线Fig.2 Curves of Wd obtained by different methods

2.2 仿真算例

在30~80 Hz 频带内按2 Hz 等间隔取频率，生成幅值为m/s2、初始相位随机的26 组单频加速度正弦信号。各频率成分的均方根为1 m/s2，计权均方根即为计权因子数值，如图3 所示。将上述26 组信号加法混合，并按400 Hz 采样率生成仿真算例，以验证本方法的计算精度和计算效率，仿真振动加速度信号如图4 所示。

图3 各频率成分的计权均方根Fig.3 The weighted-rms of each frequency component

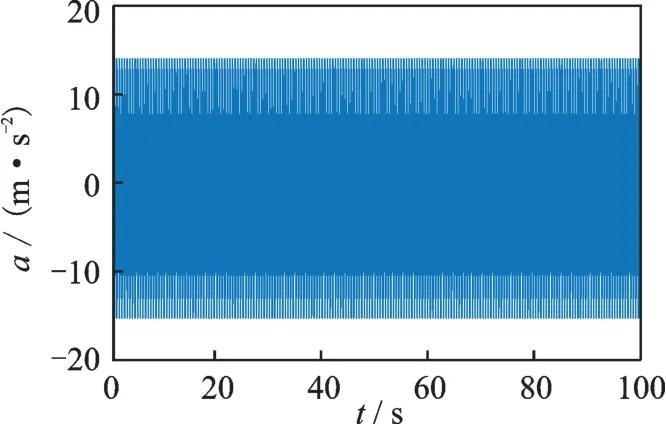
图4 仿真振动加速度信号Fig.4 The simulated acceleration signal

以Z 振级（Wk计权）的计算为例，采用不同方法估计出的瞬时Z 振级曲线如图5 所示。其中，理论值由26 组频率分布在1/3 倍频程带内的数据乘以对应的计权因子求得，滤波法计算值采用等百分比带宽滤波器分别滤出各1/3 倍频程带内的时域数据并乘以对应的计权因子求得。

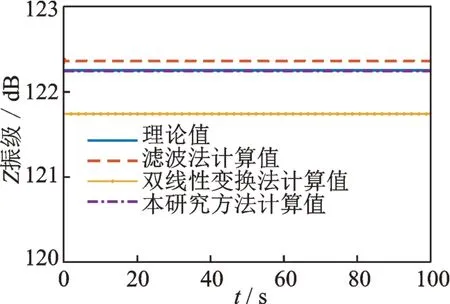
图5 不同方法估计出的瞬时Z 振级曲线Fig.5 Instantaneous VLz values computed by different methods

由图5 可知，本研究方法的计算精度与滤波法相近，均明显高于双线性变换法，这是由于采用双线性变换法进行连续-离散转化时产生误差造成的。为检验各方法的计算效率，对5 组分别为200，400，800，1 600 和3 200 s 采样长度的数据进行振级计算，不同数据长度下各方法的计算效率对比如图6 所示。

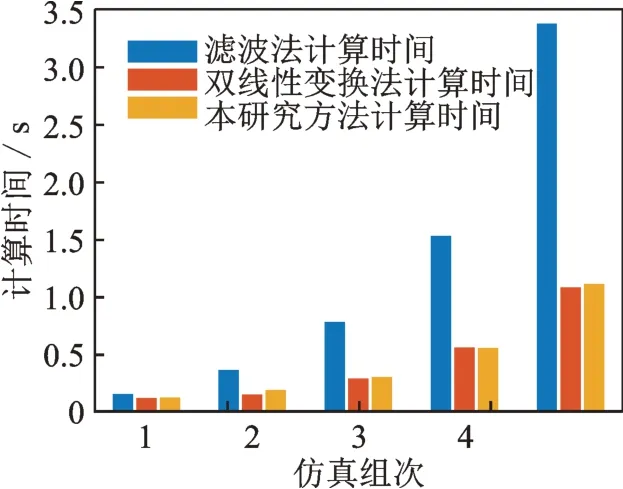
图6 不同数据长度下各方法的计算效率对比Fig.6 Calculation time of the methods under different data length

由图6 可知，本研究方法具有与双线性变换方法相近的计算效率，即处理长样本数据的速度明显高于传统的滤波法。

2.3 实测算例

根据《环境影响评价技术导则-城市轨道交通》［3］中的规定，实测南京某地铁隧洞壁的振动源强，测试现场如图7 所示。采用无人值守采集设备采集数据，连续测试17 趟列车经过时的垂向加速度信号。

图7 测试现场Fig.7 Test scene

设积分周期为1 s，步进时间间隔为0.1 s，基于图8 所示的实测加速度信号，分别采用滤波法和本研究方法计权计算瞬时Z 振级，并取每趟列车经过时的最大值连成曲线，两种方法估计出的最大Z 振级和计算时间对比分别如图9，10 所示。

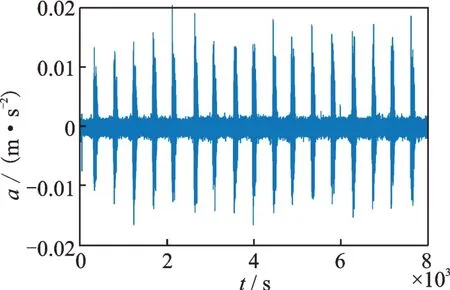
图8 实测加速度信号Fig.8 Measured acceleration signal

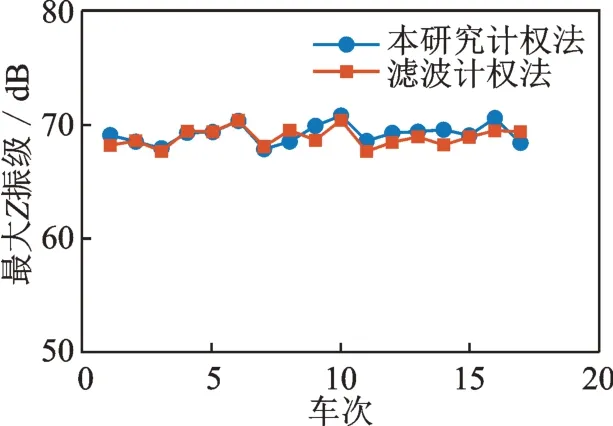
图9 两种方法估计出的最大Z 振级Fig.9 Maximum Z-Vibration level computed by two methods

图9 中2 条最大Z 振级曲线近乎重合，表明两种方法计算的精度相近。图10 结果显示，本研究方法的计算速度约为滤波法的7 倍。实测算例进一步证明，所提出的计权计算Z 振级的方法，在兼顾了计算精度的同时，明显提高了计算效率。

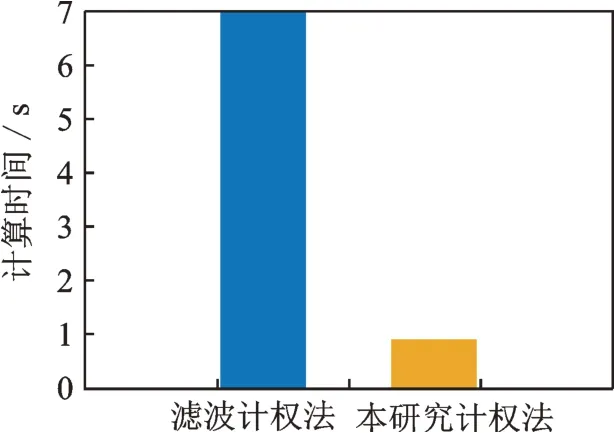
图10 两种方法的计算时间对比Fig.10 Calculation time of two methods

3 结 论

1） 通过单输入-单输出离散状态空间模型完成加速度数据的计权，过程中避免了1/3 倍频程的转换，有效提高了计算效率，并为实时加速度数据计权提供了算法依据。

2） 本研究方法使用最小二乘复频域拟合的方法获得离散状态空间系统的参数，在不增加采样频率的前提下，使离散系统和连续系统的频响幅值在关心频带内的误差最小，提高了计算精度。

3） 所提出的计权方法由时域内离散序列的输入-输出模型实现，能够实时进行加速度数据的计权计算。