基于MICA的声级计频率计权数字IIR滤波器设计

唐求，吴娟，邱伟，沈洁，滕召胜

（湖南大学 电气与信息工程学院，湖南长沙410082）

人耳对响度相同、频率成分不同的声音产生不同的听觉感受，为了模拟人耳的听觉特性，需在声级计中设计一种频率计权网络修正声音信号，使其对不同频率信号具有与人耳相同的灵敏度[1].因此，频率计权是声级计实现噪声测量的一项重要计量指标[2].IEC 61672规定1级声级计必须实现A、C频率计权功能[3].

近年来，全数字式声级计得到广泛应用[4]，但针对声级计频率计权数字滤波器的设计研究较少.频率计权数字滤波器的实现可以选择无限冲激响应（IIR）数字滤波器和有限冲激响应（FIR）数字滤波器[5].对于相同的滤波精度，与FIR滤波器相比，IIR滤波器所用的阶数少，存储单元也较少[6].

由于声级计的频率计权算法采用嵌入式系统实现，要求计算量小，占用存储空间少，故本文选用数字IIR滤波器设计频率计权.其中，常用双线性变换（Bilinear Transformation，BT）设计数字IIR滤波器[7].但双线性变换是一种近似变换，存在固有的频率失真[8]，导致误差较大.为此，文献[9]采用粒子群优化算法（Particle Swarm Optimization，PSO）对A计权的数字IIR滤波器系数进行搜索优化，取得了明显成效.但PSO算法在优化过程中容易出现早熟收敛而陷入局部极值点，从而得不到全局最优解[10-11]，尤其在加噪环境下，误差更为明显.

帝国竞争算法（Imperialist Competitive Algorithm，ICA）在滤波器的优化设计中，全局搜索能力和信息不依赖能力均高于其他智能优化算法[12].但该算法在系数搜索过程中也同样存在早熟收敛等不足，导致优化结果存在误差[13].据此，本文提出一种改进帝国竞争算法（Modified Imperialist Competitive Algorithm，MICA）的声级计频率计权数字滤波器设计方案.MICA在标准ICA算法的同化过程中添加混沌函数来增强算法的搜索可能性，引入克隆进化算子来有效引导算法向最优解方向搜索，最终得到滤波器的最优系数.相比标准ICA，MICA具有搜索范围广，寻优精度高和优化性能好等特点.

本文针对双线性变换法实现声级计频率计权存在的误差，通过在ICA算法中添加混沌函数和引入克隆算子，设计MICA算法，并将MICA应用到频率计权数字IIR滤波器设计中.仿真与实验数据表明，在加噪环境下，不同声信号级进行的频率计权误差均能维持在10-2dB数量级范围内，符合1级声级计的设计要求，证明了该方法的有效性.

1 基于双线性变换的频率计权原理与误差

1.1 频率计权原理

根据IEC 61672标准给出的A、C计权计算式，可分别推导出A、C计权模拟滤波器传递函数分别为[2]：

子滤波器传递函数Hi（s）（i=1，…，4）为：

且f1=20.6 Hz，f2=107.7 Hz，f3=737.9 Hz，f4=12 194 Hz.

标准定义下的A、C计权表达式分别为：

式中：WA1000=-2.000 dB；WC1000=-0.062 dB；f为信号频率.令z=ejwi，s=jΩi，代入双线性变换

式中：Ts为采样周期.模拟截止角频率Ωi与数字截止角频率ωi的关系为：

将式（1）（2）从s域映射到z域，利用式（6）（7），得到基于双线性变换的A、C计权滤波器传递函数.

式中：

基于双线性变换的A、C计权表达式分别为：

声级计一般采用48 kHz的采样率[14]，频率测量范围为10～20 kHz.在该频率范围内，根据文献[3]给定的34个标称参考频率点，利用MATLAB对基于双线性变换的A、C计权式（11）（12）进行仿真，并与标准A、C计权式（4）（5）进行对比.A、C计权仿真曲线分别如图1和图2所示.

图1 A计权仿真曲线Fig.1 A-weighting simulation curves

图2 C计权仿真曲线Fig.2 C-weighting simulation curves

从图1和图2中局部放大图可清晰地观察到，基于双线性变换的A、C计权在大于13 kHz的高频段都严重偏离了标准计权曲线，导致误差较大.

1.2 频率计权误差分析

定义基于双线性变换的A、C计权与标准计权的误差为：

将式（4）（5）（11）（12）分别代入式（13）可得出A、C计权的误差表达式：

式中：i=1，2，3，4.即A计权误差为4个子滤波器HBTA1（z）～HBTA4（z）的误差加权和，C计权误差为子滤波器HBTC1（z）与HBTC4（z）的误差和的2倍.基于双线性变换A、C计权子滤波器误差的幅频响应曲线分别如图3和图4所示.图3中EBTA123（f）为子滤波器误差EBTA1（f）～EBTA3（f）之和.

图3 A计权EBTA123（f）和EBTA4（f）曲线Fig.3 A-weighting curves of EBTA123（f）and EBTA4（f）

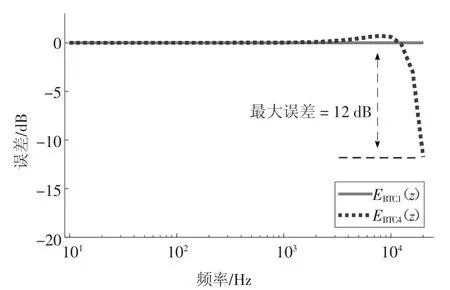
图4 C计权EBTC1（f）和EBTC4（f）曲线Fig.4 C-weighting curves of EBTC1（f）and EBTC4（f）

由图3和图4可知，基于双线性变换的A、C计权数字滤波器的误差都主要来源于子滤波器HBT4（z）.在频率为20 kHz处，HBT4（z）的最大误差接近12 dB.分析式（1）（2）可知，在C计权的基础上加上两个一阶子滤波器HBT2（z）HBT3（z）可实现A计权.因此，本文重点对A计权子滤波器HBT4（z）进行优化设计，实现步骤及测试过程均以A计权为例.

2 基于MICA的频率计权数字滤波器设计

2.1 改进帝国竞争算法

帝国竞争算法（ICA）是一种新型智能优化算法[15].该方法模拟帝国与殖民地之间相互选择与竞争，最终剩下最强的帝国，即收敛得到最优解.但在滤波器的优化设计中，ICA在系数搜索过程中存在早熟收敛的问题，导致寻优结果存在误差.

在标准ICA的帝国同化操作中，子群的每一个非理想解（殖民地）都过于直接地向子群的最优解（帝国）方向靠近，造成搜索范围过小、容易陷入局部最优的问题.为增大搜索范围，优化搜索精度，针对频率计权参数优化问题，本文提出一种改进的帝国竞争算法，该方法在殖民地向帝国移动的过程中添加各种形式的混沌函数，并筛选出优化效果最好的函数更新标准ICA的同化方程，即

式中：colold和colnew分别表示移动前后殖民地的位置；β为大于1的系数；d为殖民地与帝国之间的距离；U表示均匀分布；V1为该殖民地向帝国移动方向的一个单位向量；θ为移动的随机角度偏移量；V2为与V1正交的随机单位向量.

帝国竞争算法利用殖民地向帝国移动进行局部搜索，该操作体现的是帝国之间的信息交互，每次迭代仅仅是将最弱帝国中的最弱殖民地添加到最强帝国中，对每个帝国势力大小影响不大.因此，针对帝国之间的交互性不足，本文引入克隆进化算子，得到MICA.下面对该算子进行描述.

第1步克隆.将当前迭代次数下的m个帝国按势力大小降序排列，作为待克隆群体.每个帝国克隆个数NCloi与其所属殖民地数量NColi有关，表示为：

式中：λ为克隆系数.

第2步变异.根据式（19）（20），第i个帝国的克隆群体Cloi发生变异，成为变异群体Muti：

式中：ωi为变异概率，势力越大的帝国变异概率越小；Impbest为当前迭代次数下势力最大的帝国；n为优化问题的维度；rand（NCloi，n）为NCloi×n维矩阵.

第3步交叉.将Muti随机分为4组进行交叉：

第4步选择.选择Muti和Croi中势力最大的k个个体取代当前最弱的k个帝国.

2.2 声级计频率计权的MICA优化对象设计

由1.2节分析可知，子滤波器HBT4（z）是双线性法设计频率计权滤波器的误差主要来源.利用MICA对A计权的数字滤波器系数进行搜索优化.

根据式（8）和式（10）设计MICA优化模型：

式中：A0为增益；a0、a1与b0、b1分别为滤波器的零点和极点.为保证设计的滤波器的稳定性，极点的搜索范围取（-1，1），为方便起见零点的搜索范围取[-1，1].

增益A0由滤波器系数推导得到，即

其频率响应为：

理想滤波器H4（s）的频率响应为：

采用频域均方误差作为设计频率计权滤波器的最优化准则，误差值越小则优化效果越好.利用MICA对理想滤波器进行逼近，在34个标称参考频率点处，设计的滤波器幅频响应与理想的幅频响应均方误差为：

利用MICA对频率计权滤波器进行优化设计，将式（26）作为优化目标函数，对滤波器系数a0、a1、b0、b1搜索求解，则优化后的滤波器传递函数与A计权表达式变为：

基于MICA的频率计权数字滤波器设计框架如图5所示.首先初始化MICA算法，然后采用MICA算法在对目标函数进行参数迭代寻优直到达到对应的停止条件，从而求解出目标函数的优化参数.

具体步骤为：

1）初始化帝国集团.随机生成Npop×4维矩阵的初始位置，MICA主要参数设置为：国家数量Npop=88、帝国数量Nimp=8、殖民地数量Ncol=80、最大迭代次数Miter=800、当前迭代次数Niter=0以及数字滤波器采样频率fs=48 kHz.

图5 基于MICA的声级计频率计权滤波器设计框架Fig.5 Flowchart for the frequency weighting filter in sound-level meter based on MICA

2）帝国同化.殖民地国家按照式（17）向所属帝国方向移动.并重新计算殖民地的势力，若其势力大于所属帝国势力，则两者互换位置.

3）帝国竞争.帝国的总势力计算式为：

式中：TCi为第i个帝国的总目标函数值，其值越小，表示势力越大；ci为该帝国的目标函数值；系数ξ为小于1的正数；后一项为该帝国拥有的殖民地目标函数均值，其中f（colj）为殖民地colj的函数值，NColi为其拥有的殖民地数量.根据式（18）～（21）通过克隆进化将势力最强的k个帝国取代势力最弱的k个帝国.

4）算法收敛.累积迭代次数Niter=Niter+1，当迭代次数达到最大迭代次数Miter或者通过帝国竞争后，最弱帝国逐渐灭亡，最终只剩一个帝国集团.此时的群体为算法最优解，搜索终止.

5）得到全局最优位置处的Hopt（z），根据式（27）（28）求出基于MICA算法的A计权WMICA.A（f）.

2.3 仿真分析

为验证本文提出的MICA设计声级计频率计权数字滤波器的有效性，利用MATLAB进行仿真生成仿真数据.定义基于MICA的A计权的误差为：

图6为基于MICA算法的A计权误差EOPTA（f）与基于双线性变换的A计权误差EBTA（f）的幅频响应曲线，在局部放大图中，黑色曲线放大的是从10～10 000 Hz的基于MICA的A计权误差.由图6可知，本文提出的MICA设计方法能有效减小双线性变换设计频率计权数字滤波器的误差，且误差范围能控制在10-3dB的数量级范围内.

此外，为了比较算法相比传统优化算法的性能，同时采用PSO和标准ICA算法进行了频率计权滤波器优化对比设计[16].算法的迭代次数均设置为800，仿真结果的误差幅频响应曲线如图7所示.仿真结果表明，与PSO和ICA优化算法相比，在相同的迭代次数下基于MICA设计的滤波器误差更小，具有更好的优化性能，同时证明了本文改进算法的有效性.

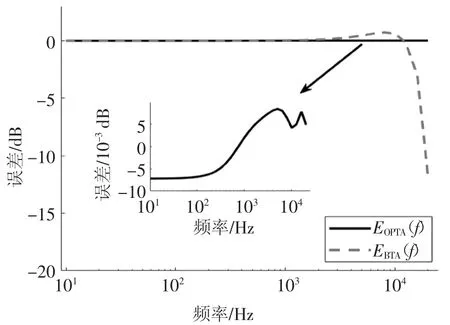
图6 基于MICA的A计权误差曲线Fig.6 Error curve of A-weighting based on MICA

图7 A计权误差曲线Fig.7 Error curves of A-weighting

3 实验测试分析

为验证所提出的改进ICA声级计频率计权滤波器设计方法的有效性，本文采用如图8所示的声级计实验平台进行测试.其中，信号发生单元由信号源与可变衰减器构成，利用调理电路对电信号进行调理，采用最高采样频率达450 kHz的16位中泰工控EM-9118B-18同步数据采集卡对电压信号进行采集.最后，通过以太网TCP/IP协议传输方式将数据实时传输至PC机进行显示和管理、以及噪声数据的分析等.

图8 声级计实验测试平台Fig.8 Test platform for the sound-level meter

为了测试声级计在不同信号级下的A计权特性，在输入信号级为L={128，118，98，78}dB 4种情况下测试声级计A计权误差.表1给出了标称参考频率点处基于双线性变换、PSO、ICA和MICA的声级计A计权在低频段和高频段的测试误差.同时，为了反映算法的抗噪性，给不同信号级声源添加信噪比为25 dB的高斯白噪声信号.图9、图10分别给出了频率在10 Hz～20 kHz内的34个标称参考频率点处基于双线性变换与MICA的A计权测试结果曲线.

图9 基于双线性变换的A计权测试结果曲线Fig.9 Curves of the test result of A-weighting based on BT

A计权的测试结果分析如下：

1）由图9可知，双线性变换设计的A计权在4种输入信号级处的测试误差主要来自于低频段和高频段.根据2.2节所知，高频误差主要来源于双线性变换法的非线性变换；低频段的误差来源于文献[3]规定，当输入为78 dB的信号时，低于12.5 Hz的信号经过A计权后至少衰减63.4 dB，即声级将小于14.6 dB，该输入信号级的低频段误差主要受本底噪声的影响，故本文对此未做考虑.

表1 声级计在低频段和高频段的A计权测试误差（SNR=25 dB）Tab.1 A-weighting test error of the sound-level meter in low&high frequency（SNR=25 dB）

2）由图10可知，基于MICA的A计权在高频处的误差得到了极大改善.特别是表1中，在噪声环境的影响下，MICA的测试精度均优于PSO和ICA，且MICA的测试误差基本能维持在10-2dB数量级范围内，具有良好的抗噪性，符合声级计0.1 dB的精度设计需求.

图10 基于MICA的A计权测试结果曲线Fig.10 Curves of the test result of A-weighting based on MICA

4 结论

本文针对双线性变换法设计声级计频率计权数字滤波器时出现误差较大的问题，提出了一种基于改进帝国竞争算法的声级计频率计权数字IIR滤波器设计方法.为避免标准ICA早熟收敛而陷入局部最优，在同化阶段加入混沌函数以及帝国竞争阶段引入克隆进化算子，进一步提高算法的收敛精度.对A计权的测试结果表明，本文提出的改进ICA算法，有效改善了双线性变换法的误差，优化效果明显.且在加噪环境下，不同声信号级的计权误差均能维持在10-2dB数量级范围内，符合1级声级计设计要求.本文提出的方法不仅适用于声级计的频率计权优化设计，也适用于其他采用双线性变换设计数字滤波器引起的频率特性失真问题，具有较高的实际应用价值.