轨道车辆扇形压电阵列式俘能器宽频响应设计∗

钟倩文， 郑树彬， 孙佳慧， 彭乐乐， 文 静

（上海工程技术大学城市轨道交通学院 上海，201620）

引 言

随着超大城市及其线网规模的不断扩大，要求轨道交通安全运维行业向低碳化、智能化方向发展，轨道安全监测（structural health monitoring，简称SHM）设备从传统有线技术向先进无线技术转变［1-2］。轨道交通车辆的运行间隔短、密度高且连续运行，列车车辆引起的振动是一种清洁、连续及稳定的能源，具有为SHM 设备供电的巨大潜力。压电式俘能器具有结构简单、制作方便、抗干扰能力强、能量密度和能量转化率较高等优点，是一种有巨大潜力的技术［3］。

具有多种振动模式的俘能器可以在更宽的频率范围内发生共振，以形成具有多个共振峰的多自由度（multi-degree of freedom，简称DOF）为主要特征，从而提高环境能量获取效率。刘久周等［4］在基于同步开关电路的压电悬臂梁中引入副梁，大大提升了能量收集效果。王光庆等［5］设计了的带弹簧的双自由度系统，其工作频带提高至单自由度系统的2 倍。Nie 等［6］采用L 形压电组合梁，有效地在更宽的频带上采集能量，并减少振动位移。此类DOF 系统能匹配的共振频率有限，经常引入非线性因素，因此结构复杂，不易设计、制造和维护，安全性不足。悬臂梁阵列也是一种常见的解决方案。田晓超等［7］对4 个压电悬臂梁阵列俘能器的发电性能进行了研究，响应频带拓宽至77 Hz，且空间利用率高。罗翠线等［8］使用3×5 矩形悬臂梁阵列，拓宽了响应频带。Xue 等［9］提出一种10 个不同厚度串联连接的双晶悬臂梁阵列，比单个梁最大输出功率高出10 μW。Kherbeet 等［10］研究发现，无论是水平还是垂直排列，串联三角梁阵列比单悬臂梁获得更大的功率。阵列式悬臂梁结构简单，且可以匹配相对多的谐振频率，取得较好的发电效果。综上所述，采取将多个一阶固有频率相近、能量转化效率较高的压电俘能单元集成在同一结构框架上形成阵列，是设计低频、多源及宽频压电俘能器的有效方案。

笔者基于上海地铁列车采集的轴箱振动信号，采用有限元分析方法提出了一种具有12 个梁单元的圆盘阵列采集系统，并搭建了振动测试平台验证了设计方案的有效性。通过改变压电梁阵列的设计参数，使得悬臂梁单元的固有频率分别与多个振源集中频率相匹配，提高压电式俘能器的输出性能。

1 扇形压电阵列结构及理论建模

1.1 阵列式俘能器结构设计

由于在轨道交通车辆运行环境下，振动频率往往随着车辆的变速运行而产生多个频率峰值，而悬臂梁由于其结构特点，一般只能在单个频率点上与环境频率产生较强的共振。阵列设计可以引入多个具有不同固有频率的梁单元，这些梁单元的工作频率彼此重叠，使得系统整体呈现宽频特性。悬臂梁单元的能量转化效率越高，阵列俘能器整体的输出性能就越好。已有多项研究表明［11-12］，增加固定端相对于自由端的宽度，即采用三角形、扇形及梯形等形状的悬臂梁结构，相比于矩形表面，可以获得更高的单位面积挠度及应变能。扇形悬臂梁以弧边作为固定端，相比于相同有效面积的三角形和矩形，最大应力较小，分布更均匀，增强了结构在持续振动环境下工作的可靠性，圆形阵列设计则提高了空间利用效率。因此，引入扇形双晶悬臂梁作为阵列结构的基本单元。

扇形压电悬臂梁圆形阵列结构如图1 所示，由多个总顶角和为360°、圆半径长度R和顶角θ一致的扇形悬臂梁阵列组成一个完整的圆盘结构。每个扇形悬臂梁单元中间由厚度为hs的金属基底层、基底上下两面对位黏贴厚度为hs的压电陶瓷层以及宽度固定、质量为Mt的末端质量块组成，三者的接触面由环氧树脂胶合成为一个连续整体。质量块所在端为自由端，被双层圆环夹紧固定的弧形长边为固定端。当阵列结构发生受迫振动时，悬臂梁发生弯曲变形，通过正压电效应在垂向表面聚集大量自由电荷。

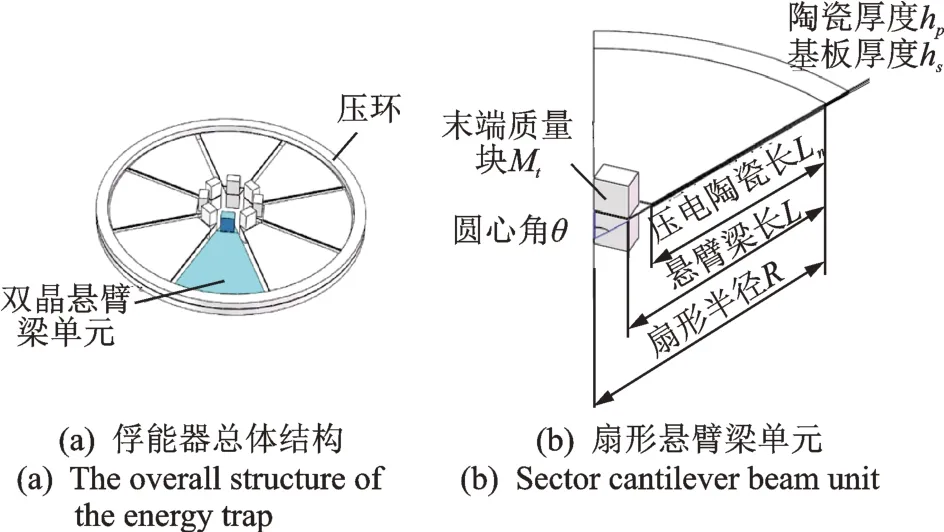
图1 扇形压电悬臂梁圆形阵列结构图Fig.1 Structure diagram of circular array of sector-shaped piezoelectric cantilever beams

扇形悬臂梁阵列式压电俘能器宽频设计路线如图2 所示。首先，建立压电悬臂梁的分布参数模型及有限元参数模型，经过对比验证及参数分析，得到了影响梁输出性能的多个结构参数，并获得了关键参数与输出的关系；其次，采集上海地铁车辆轴箱振动信号，分析其振动特征，明确宽频设计最终目标；最后，通过实验和仿真对结构的频率响应特征进行测试与分析，验证设计方法的可行性。

1.2 压电耦合分布参数模型

本研究建立的压电耦合分布参数模型相比于广泛采用的一般激励下的集中参数模型具有更高的预测精度［13］。扇形压电悬臂梁单元受力原理如图3 所示，其中：x，y，z轴分别对应d31模式下的1，2，3 方向；x轴与梁的中性层共面；z 轴为极化轴。用于胶合的环氧树脂聚合物材料，其弹性模量远低于压电陶瓷和大多数金属材料，因此在建模过程中忽略不计。悬臂梁厚度和长度之比很小，可以忽略剪切变形和转动惯量的影响，符合欧拉-伯努利（Euler-Bernoulli） 梁的假设。

图3 扇形压电悬臂梁单元受力原理图Fig.3 Schematic diagram of the force of a sector-shaped piezoelectric cantilever beam unit

当悬臂梁受到自由端集中力的作用发生弯曲变形时，梁的变形可以描述为横向位移g(t)和环向转角位移h(t)的叠加。梁的基础横向形变wb(x，t)可以描述为

连续振动激励下，双晶悬臂梁受迫振动方程为

其中：cs I为内部应变率；ca为黏性空气阻尼系数；m为单位长度梁的质量；Mt为自由端末端质量；δ(x)为狄拉克函数；R为扇形梁的半径；M(x，t)为不包含应变率阻尼效应的内部弯矩。

其中：b(x)为梁随半径方向变化的宽度，b(x)=为PZT-5H 的 厚 度；hs为金属基板的厚度；T1p，T1s分别为压电层和金属层在x方向上的应力分量。

根据金属和压电的本构方程可得

其中：Ys为金属层弹性模量；Ss1为金属层的轴向弯曲应变；cE11为压电陶瓷在常电场下的弹性模量，对于压电薄梁有为常电场条件下的弹性柔度；Sp1为压电层的轴向弯曲应变；e31为有效压电应力常数，，d31为 压电应变常 数；E3为z轴方向的电场分量。

对于串联情况下的压电陶瓷输出电压v，短路状态下满足，由于两层陶瓷的电荷极化方向相反，故而产生同方向的瞬时电场设模态阶数r=1，2，3，则wrel的本征收敛级数表示为，其中：ϕr(x)为3 阶模态的质量归一化函数；ηr(t)为串联构型的模态坐标。展开如下

其中：Ar为模态幅值常数；λr为r阶特征值。

压电陶瓷串联条件下的模态机电耦合项θr和等效电容Ceq分别为

将式（7）~（9）代入受迫振动方程（2），得

截面质量m和根据平行轴定理得到的末端质量惯性矩It分别为

复合截面的弯曲刚度在短路条件下为

解得特征值后可计算短路条件下r阶无阻尼固有频率ωr为

可以进一步求得阵列系统的稳态电压响应为

其中：Rt为负载电阻。

2 轨道车辆轴箱振动特征分析

出于行车安全考虑，将压电俘能装置安装在轴箱上，收集轮轨冲击产生的垂向振动能量；加速度传感器固定于车辆轴箱部位，收集上海地铁某型车在测试线路以50 km/h 匀速行驶的振动信号并分析其特征。使用的测试设备主要有DFT1301 型三轴加速度传感器及采样频率为10 kHz 的Wavebook516E数据采集仪。信号采集如图4 所示。

图4 信号采集Fig.4 Signal acquisition

对采集到的垂向加速度信号进行傅里叶变换，结果如图4（a）所示。在轴箱处可俘获的垂向振动主要在0~300 Hz 频段内有较密集的分布，呈现宽频、低幅值、多模态的特点。在0~300 Hz 振动范围内，整体振幅较大，且集中分布在20.95，40.45 和204.19 Hz 处。因此，采用机械调谐策略［13］，改变压电悬臂梁的结构设计参数以逐个调整其机械特性，使其与轨道车辆轴箱部位的环境振动频率相匹配，以提高发电效率。

3 悬臂梁结构参数与模态频率的关系

3.1 有限元模型

由1.2 节中建立的扇形悬臂梁分布参数模型可知，俘能器发电性能、工作频率与多个材料参数及结构参数有关，悬臂梁所用材料参数如表1 所示。金属基底材料选用弹性模量大的铍青铜，在冲击下不易产生塑性形变。压电陶瓷选用PZT-5H，其物理强度高、化学惰性强且制造成本相对较低，被广泛用于振动冲击条件下的压电能量收集器件。

表1 材料参数表Tab.1 Material parameter table

结构参数包括圆周外廓半径R、顶角度数θ、陶瓷厚度hp和长度Lp、基底厚度hs和长度L以及末端质量Mt。当同层阵列悬臂梁单元的顶角θ和为360°、外廓半径R相等时，可以拼合为一个完整的圆周，厚度可以通过增加绝缘垫片来弥合。

为建立结构参数与模态频率的函数关系，获得各参数与压电悬臂梁性能之间的关系，利用ANSYS 仿真软件建立上述结构参数的有限元模型，进行模态分析和谐响应分析。理论结果与有限元仿真模型如图5 所示，由图可知，参考实际测得的轴箱载荷谱和车载环境下悬臂梁的受力计算原理［14］，在z轴方向施加2g的加速度，在相同参数设置下，分布参数理论模型与ANSYS 仿真模型得到的开路电压峰值与谐振频率吻合误差在5%以内。

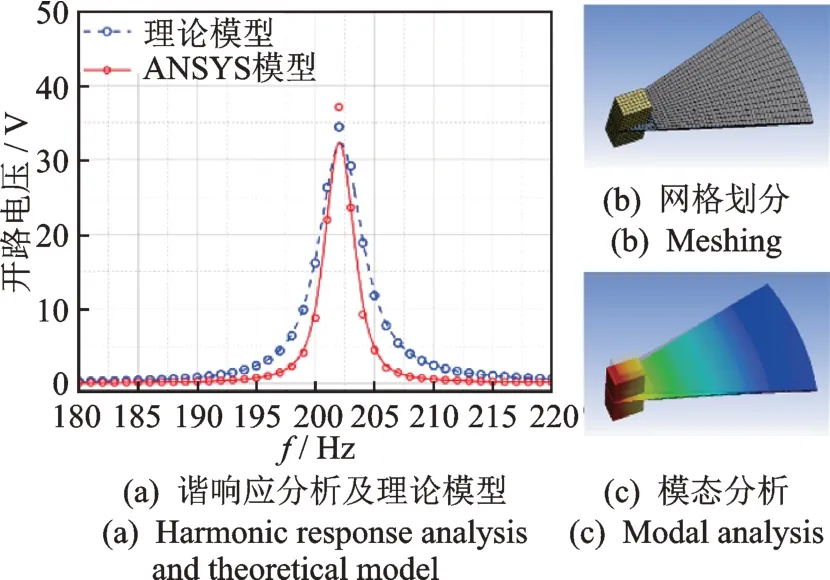
图5 理论结果与有限元仿真模型Fig.5 Model of theoretical results and finite element simulation

3.2 结构参数分析

阵列式俘能器的每个单元具有相同的顶角值和外廓半径，保持以下参数不变：hp=0.2 mm，hs=0.2 mm，Mt=5g，L=50 mm，Lp=20 mm，在相同的取值间隔下改变所建立的有限元模型的参数θ和R，变化范围为15°~75°和60~110 mm 之间的离散数据。通过多次谐响应分析得到单个变参数对模态频率及输出电压峰值的影响，开路电压、谐振频率与顶角、外廓半径的关系如图6 所示。由图6（a）可知：在一定范围内，梁的谐振频率随着顶角的增大而增大，增加范围在0~65.65 Hz；输出电压在30°时存在极值，这是因为顶角越小，扇形弧边宽度b也变小，导致弯曲刚度变小，谐振频率变低，电能转换率相应提高；b减小到一定程度后，陶瓷发电面积减小的效应会大于转换率提高的效应。因此，顶角的调整可以折中改变梁单元的谐振频率和输出电压。

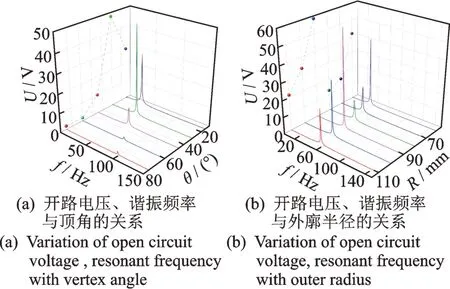
图6 开路电压、谐振频率与顶角、外廓半径的关系Fig.6 Variation of open circuit voltage and resonant frequency with vertex angle and outer radius

由图6（b）可知：在一定范围内，梁的谐振频率随着R的增大而增大，增加范围在0~21.04 Hz；输出电压随R在60~80 mm 及90~110 mm 之间递减。这是因为在其他条件不变的情况下，R的增加一般会使自由端位移增大，当R增加到对平均应力的影响大于自由端位移对平均应力的影响时，输出电压会减小。因此，外廓半径R的调整也可以改变梁单元的输出性能。

3.3 宽频结构设计与仿真验证

由单结构参数分析结果可知，压电悬臂梁阵列的模态频率f1与结构参数θ和R具有明显相关性。频率匹配后的压电阵列仿真如图7 所示。为了实现轨道车辆用扇形压电悬臂梁阵列的宽频响应设计，悬臂梁单元采用#n表示，R=60 mm，θ=30°。为匹配表2 中提出的3 个目标频率，通过迭代逼近的数值 计 算 方法［15］设计 了3 种、共12 个优 化 悬 臂 梁单元，具体结构参数如表2 所示。

表2 结构参数表Tab.2 Structure parameter table

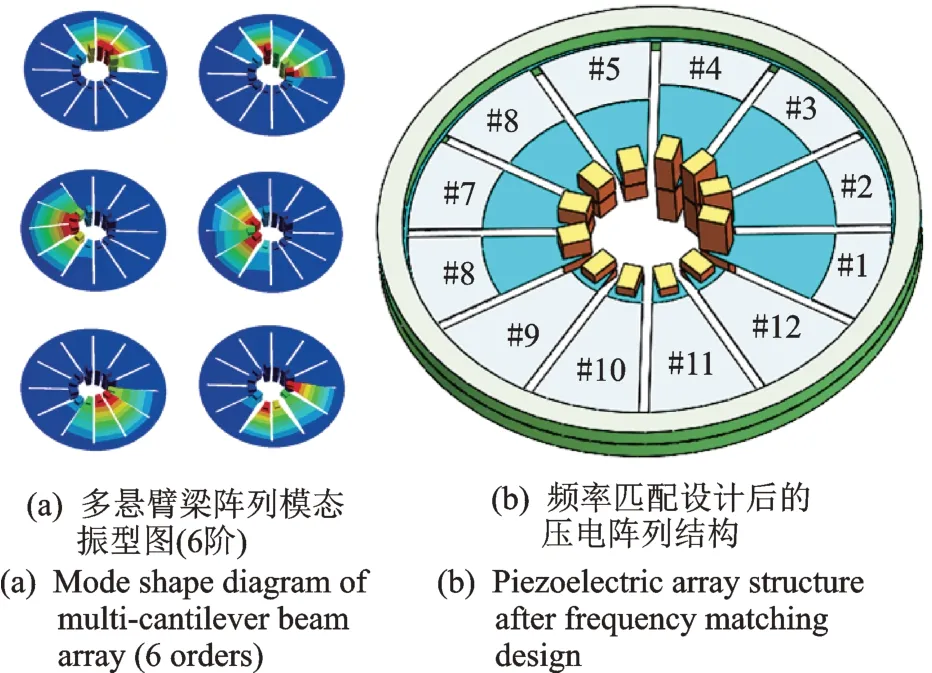
图7 频率匹配后的压电阵列仿真Fig.7 Piezoelectric array after frequency matching

将表1、表2 的数值代入参数化有限元模型，在ANSYS 中通过完全法对结构进行谐响应分析，设定垂向加速度载荷为2g，建立了如图7 所示的优化阵列的有限元模型，获得的3 种梁单元对应的仿真工作频率如表3 所示，扇形梁单元的工作频率与目标基本一致。

表3 仿真工作频率Tab.3 Simulation operating frequency

前12 阶多悬臂梁阵列谐振频率变化曲线如图8所示。由图7，8 可以看出：悬臂梁单元在前12 阶频率内能产生所需的垂向弯曲振型，单元利用率为100%；前12 阶低频频率变化范围大约为 21.07~56.75 Hz，频带宽度达到35.68 Hz，可知多悬臂梁压电振子能有效拓宽其工作频率范围。通过分析结构参数，可以使其前3 阶模态频率与列车振动主频相匹配。

图8 前12 阶多悬臂梁阵列谐振频率变化曲线Fig.8 First 12 orders variation curve of resonant frequency of multi-cantilever beam array

进一步进行谐响应分析，得到在0~250 Hz 频率范围内，轨道车辆用扇形压电悬臂梁阵列频率响应如图9 所示。与上海地铁某线车辆轴箱振动信号频率谱密度图对应可知，其频率响应与表2 中车辆轴箱振动特征相匹配。

图9 轨道车辆用扇形压电悬臂梁阵列频率响应图Fig.9 Frequency response diagram of sector-shaped piezoelectric cantilever beam array for rail vehicles

4 实验验证

为验证所设计俘能器的发电性能，搭建了如图10 所示的振动测试系统，轨道车辆运行时轴箱产生的振动由激振器模拟给出。系统由信号发生器、功率放大器、数字示波器、激振器、压电梁及计算机组成，压电梁固定在振动台的支架上，通过振动控制软件设置振动激励信号为正弦扫频信号。

图10 振动测试系统Fig.10 Vibration test platform

外接负载电阻，设定0~210 Hz 的扫频范围，获得输出电压实验值与仿真值对比如图11 所示。

图11 输出电压实验值与仿真值对比图Fig.11 Comparison of experimental value and simulated value of output voltage

由图11 可以看出：在10~50 Hz 之间，悬臂阵列输出电压在20.17 和40.05 Hz 出现两个共振峰，实验输出电压分别为20.07 和72.04 V；在190~210 Hz 之间，输出电压在200.37 Hz 出现一个共振峰，得到的最大输出电压为39.96 V。

结果表明，优化后的压电梁固有频率与目标宽频需求相吻合，且相对于传统单悬臂梁，增加了响应峰的数量，拓宽了谐振频带。

5 结 论

1） 提出了一种宽频响应的扇形压电悬臂梁阵列式俘能器结构，通过建立扇形悬臂梁单元的分布参数模型，分析其工作原理，得到了影响其谐振频率和电压输出性能的材料参数和7 个关键结构参数，即外廓半径R、顶角θ、基底厚度hs、PZT-5H 厚度hp、基底边长L、PZT-5H 边长Lp和末端质量块质量Mt。

2） 扇形压电悬臂梁阵列结构的设计关键在于每个悬臂梁单元的外廓半径R相等，且顶角θ的总和为360°。通过对离散点处参数取值的梁进行有限元分析，发现了R和θ值与谐振频率和电压输出性能之间的关系，最终选择R=60 mm 和θ=30°作为折中解。

3） 为了匹配轴箱低频振动集中处的多个频率峰值，提出了同阵列内3 种规格的扇形悬臂梁圆盘设计，编号分别为#1~#4，#5~#8 和#9~#12，每4个梁单元的结构参数完全一致，可使阵列俘能器在20.95，40.45 与204.19 Hz 处附近产生响应，使结构的前12 阶谐振频率宽度达到35.68 Hz。在拓宽了响应频带的同时，与地铁车辆轴箱振动特征相匹配。

4） 本研究提出的轨道车辆用扇形压电阵列式俘能器，宽频响应及输出性能良好，且可以根据不同的振动环境所定义的频率匹配目标进行针对性的优化，实现宽频、低幅及多模态的匹配设计。