设备激励下山西河津电厂结构振动测试研究∗
姚泽良, 白国良, 党发宁, 令狐恬晶, 祁亚伦
(1.西安理工大学土木建筑工程学院 西安,710048)
(2.西安建筑科技大学土木工程学院 西安,710055)
(3.西安理工大学省部共建西北旱区生态水利国家重点实验室 西安,710048)
引 言
大型火电厂空冷系统的主体结构由A 型架、钢平台和管柱3 部分组成[1-2]。A 型架由10~15 m 高的三角形钢支架组成,用于安装重达万吨的空冷设备。钢平台由4~8 m 高的纵向和横向钢桁架交叉构成,其跨度为24~28 m,悬挑为12~15 m,平台内部悬挂有数十台低频率转动的大尺寸风机(半径为4.5~5.0 m)。结构下部为多根大尺寸薄壁钢筋混凝土管柱,管柱高为30~40 m,半径为1.5~2.0 m,壁厚为0.3~0.5 m。因工艺要求,该类结构质量、刚度集中在上部,表现出上刚下柔的“高脚鸡腿式”独特体型,其跨度和悬挑均较大,受力复杂,目前对其动力问题研究仍存在不足[3]。
开展结构风机激励、地震作用及风载效应等动荷载响应研究前均需要先确定出实际结构的周期、频率、振型及振幅等自振特性[4-6]。确定结构自振性能参数的方法主要有数值计算、模型试验和现场测试。近年来,学者们在某些特殊结构的动力性状研究方面取得了许多成果[7-13]。周云等[7]对两栋高层建筑进行了随机振动测试,并采用Perform-3D 软件分别建立了3 种模型,运用获得的模态参数进行了模型修正。高延安等[8]采用自然环境激励法对古建筑进行了动力测试,获得了结构自振频率等动力特性参数。陈艳明等[9]基于现场实测数据分析了下沉式地铁车辆段内列检库振源特性和振动传播规律。华一唯等[10]基于现场动力特性测试结果对南京鼓楼建筑的有限元计算模型进行了修正。闫培雷等[11]对典型高层建筑结构的基本自振周期进行了现场测试和回归数值分析。徐璐等[12]研究了大型冷却塔的自振频率估算方法及拟合优度。文献[10-13]表明,在结构自振性能模拟计算中,计算模型常简化或忽略非承重构件和局部构造等细部,构建的模型难以完全反映结构原型的实际构成和材料性能,计算结果与实际情况存在较大差异。为了掌握大型火电厂空冷主体结构的真实动力特性,有必要对其自振性能开展现场振动试验研究。
笔者选取山西河津电厂A 型架-钢平台-管柱结构体系,利用测振仪分别对设备激励下该结构体系的扭转振动、竖向振动和水平振动进行了现场试验,利用DASP 程序对试验数据进行了时域响应分析和自谱响应分析,并结合ANSYS 计算结果,系统研究了结构的振动响应、横向位移、纵向位移、竖向位移、变形、转角、振型及频率等关键动力性能指标。
1 工程概况
1.1 试验结构
山西省河津大型火电厂空冷系统的主体结构为A 型架-钢平台-管柱结构体系,试验结构见图1。该结构体系由1 号和2 号两个完全相同的单元结构对称组成(两单元中间断开,间距为9.51 m),每个单元均为单跨、四边悬挑结构,柱网尺寸为22.80 m×26.64 m,其中南北向(横向)为4×12.465 m,东西向(纵向)为6×12.165 m。结构顶部为高13.2 m 的A形架,上部为高8.9 m 的空间交叉桁架构成的钢平台,下部为高32 m 的钢筋混凝土管柱。钢桁架为宽翼缘H 型钢,混凝土强度等级为C40,纵筋均采用HRB400 级。由于工艺需要,钢桁架内安装了24 台低频运转的大直径风机(直径为9.14 m)。因该结构1 号单元和2 号单元平面完全对称,选取1 号单元进行现场试验。
1.2 试验原理
结构动力性能试验方法主要有共振法、自由振动法和脉动法。共振法采用专有激振设备对结构的受迫振动进行测试而求得结构动力参数;自由振动法通过特定手段测试得到结构的自由振动衰减曲线,进而求得结构的基本动力参数;脉动法利用周围自然环境的微小激励测试出结构的动力特性,该方法不需专门激振器,不受结构形式和尺寸大小的限制,多用于现场试验。根据以上试验方法特点并考虑A 型架-钢平台-管柱结构的实际情况,选用脉动法对该结构的自振性能进行现场试验。
脉动法假定输入和响应均为各态历经的过程,并假定脉动信号为白噪声。当激励信号谱曲线为白谱或包含白谱且在半功率带宽内相对平坦时,谐振幅值响应被认为与纯模态响应时一致,此时振幅谱曲线峰值点对应的频率即为结构固有频率,同一固有频率处测点振幅峰值的相对大小为结构固有振型。
1.3 试验过程
本试验采用国家地震局研发的测振仪(891-Ⅱ型,频率为0.5~100 Hz),该设备包括6 个磁电式拾振器、1 台信号放大器和一套基于DASP 程序的信号采集处理系统(INV306 型)。根据试验结构的特征,设计了扭转振动(3 个测点)、竖向振动(3 个测点)和水平振动(5 个测点)3 类试验工况。其中,扭转和水平工况均测每个测点的横向和纵向两个正交水平方向的振动信号,试验中先测横向振动,之后把拾振器均同方向旋转90°后再测纵向振动。试验过程中记录风机运转速度,在数据分析处理时剔除风机运转影响。
本 次 测 试 时 间 为2020 年10 月16 日09:00 至17:00,温度为20 C°,风速为1.5 m/s,在风机正常工作条件下进行测试。通过数据采集仪对各拾振器获取的信号进行采集、量化和存储,利用DASP 程序对获得的试验数据进行时域分析和自谱分析。为提高精度和获得稳定结果,笔者将试验数据进行了平均化处理。经传递函数和功率谱分析,得出试验测点振幅谱曲线。
2 结构扭转试验
2.1 扭转测点设计
结构某处扭转振动的大小与其到扭转中心的距离有关,离扭转中心越远,其扭转振动越大。扭转振动试验的基本原理是:先利用拾振器获得结构特征位置处的水平振动位移幅值(横向和纵向),再根据实际拾振器的布置情况,选出合适的位置作为计算基点,计算分析出各测点水平振动幅值之间的角度差值或者比值,来分析结构的扭转情况。通常情况下,扭转振动试验把拾振器设计在建筑物的两侧、四角等特征位置,拾振器之间保证有一定的距离。
基于以上要求,并考虑1 号单元结构的现场情况,在该结构钢桁架平台顶部的两个角部悬挑端和柱中悬挑处设计测点用于测试结构扭转振动情况,共设置了3 个拾振器(图1),即测点1,2,3 分别布置在结构钢桁架平台顶部东北角、东南角及南悬挑边的中点。
2.2 扭转振动结果分析
对扭转测点进行了拾振器横向和纵向布置时的振动测试。图2,3 分别为扭转振动时域分析和谱分析曲线,由图可知:不同测点横向和纵向振动响应波形均不一致,表明测点振动响应与其位置有关;同一测点横向和纵向峰值发生时刻不一致,说明横向和纵向动力性能不同。

图2 扭转振动时域分析Fig.2 Time domain analysis of torsion vibration
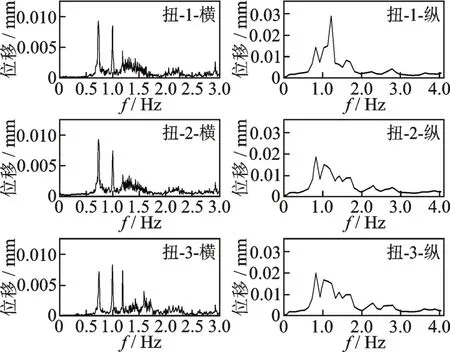
图3 扭转振动谱分析Fig.3 Spectrum analysis of torsion vibration
根据测点布置的情况,以不同测点为基点计算分析了测点位移、相对转角及转动角度差。当拾振器横向布置时,选择测点3 为基点,比较测点2 和3的位移,计算分析了测点2 绕测点3 的转动角度和方向。当拾振器纵向布置时,以测点1 为基点,比较测点2 和1 的位移,计算分析测点2 绕测点1 的转动角度和方向。扭转测点位移对比如表1 所示,其中:横向转角1 为Tan-1[(点2,3 位移差)/48 000];横向转角2 为Tan-1[(点1,3 位移差)/48 000];纵向转角1 为Tan-1[(点2,1 位移差)/50 000];纵向转角2 为Tan-1[(点3,1 位移差)/50 000];横向转角差为点2和点1 绕测点3 的转动角度差;纵向转角差为点2 和点3 绕测点1 转动角度之差。

表1 扭转测点位移对比Tab.1 Displacement comparison on torsion tested points
由表1 可知,拾振器横向或纵向布置时,结构都产生了较小转动,说明存在整体扭转现象。拾振器横向布置时结构最大转动角为1.19×10-4(°),拾振器纵向布置时最大转动角为7.19×10-5(°),说明横向扭转比纵向大。点2、点1 相对点3 的横向转角差为-1.07×10-5~1.44×10-6(°);点2、3 相对点1 的纵向转角差为-9.93×10-7~1.73×10-5(°),测点间的转角差值均较小,其最大转动差值为1.73×10-5,说明结构自身存在变形,但变形较小。
3 结构竖向振动测试
由于生产工艺的要求,结构顶部安装有昂贵的空冷设备,其对结构钢桁架平台的平整性有严格要求。为了保证电厂安全生产,需要掌握该类结构的竖向振动位移,确保空冷设备正常运行。
3.1 竖向测点布置
根据竖向振动试验的目的并考虑到现场条件的限制,竖向振动测点设计在结构的一侧悬挑及柱中悬挑部位,共布置了3 个拾振器。笔者将竖向工况测点1,2,3 均布置在结构钢桁架平台顶部南悬挑边,其中测点1 在距离钢桁架顶部西南角28 m 处,测点2 位于钢桁架顶部西南角,测点3 位于距离钢桁架顶部西南角48 m 处,竖向测点布置见图4。
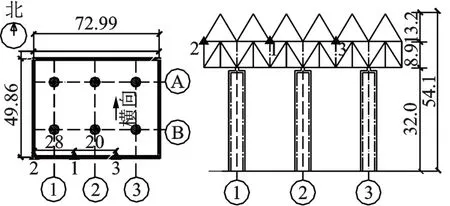
图4 竖向测点布置(单位:m)Fig.4 Tested points arrangement of vertical vibration(unit:m)
3.2 竖向振动结果分析
为了研究结构的竖向振动位移,分别对竖向测点进行了3 组振动试验。对各测点实测数据进行了时域分析、自谱分析以及测点时域波形波峰、波谷、峰峰值(波峰与波谷之差)的统计分析。竖向测点时域分析和谱分析如图5 所示,竖向时域波形对比分析如表2 所示。
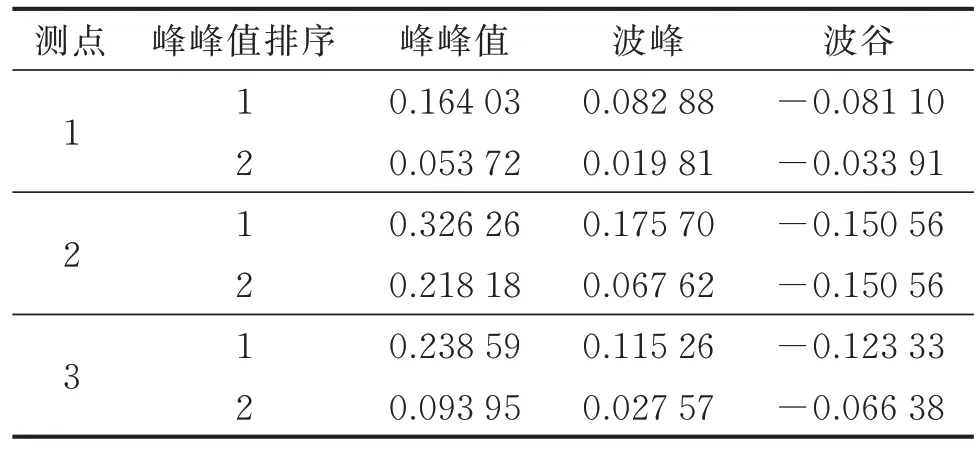
表2 竖向时域波形对比分析Tab.2 Time domain wave analysis of vertical vibration mm
由图5 可知,各测点竖向振动波形由于所处位置不同而不同。测点2 位于结构的悬挑端角部,此处竖向振动幅度最大;测点3 的竖向振动幅度比测点1 大,这是因为测点3 到东南角的距离(24.99 m)小于测点1 到西南角的距离(28 m)。可见,测点离悬挑端角部越近,竖向振动幅度越大。根据表2 数据,测点最大竖直向上振动位移为0.175 7 mm,最大竖直向下振动位移为0.150 56 m,最大竖向振动位移均发生在测点2 处,其相应的最大峰峰值为0.326 26 mm,表明结构的竖向振动位移较小,能满足钢桁架平台平整要求。
4 结构水平振动测试
4.1 水平测点布置
布置水平振动测点应考虑以下原则:水平振动测点一般布置在结构的刚度中心,以减少或避免结构自身扭转的干扰,便于仪器捕捉平移振动信号;在结构刚度突变、质量突变等特征处应布置测点,结构振动形态常与结构突变紧密相关;测点应远离局部振动部位以避免振动信号失真。
基于以上布置原则并结合结构特征,在A 型架+钢桁架+管柱结构B1 柱的A 型架顶(54.1 m)、钢桁架顶(40.9 m)、柱顶(32.0 m)、柱中(14.2 m)和柱底各特征高度处分别布置了5 个水平振动测点,水平测点布置如图6 所示。
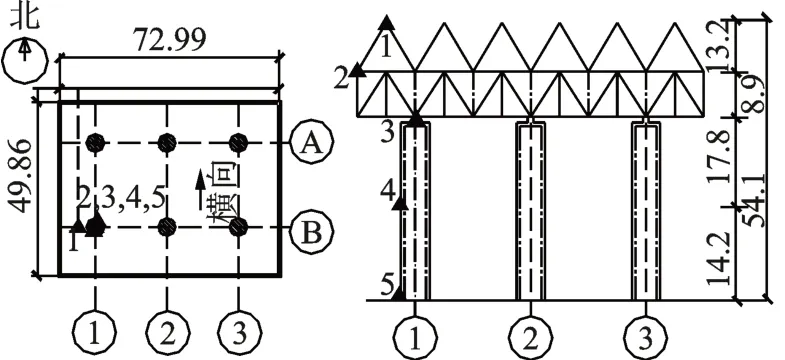
图6 水平测点布置(单位:m)Fig.6 Tested points arrangement (unit:m)
4.2 水平测试结果分析
对各测点分别进行了拾振器横向和纵向布置的试验研究。试验在正常生产条件下进行,现场记录的风机转速为72 r/min,即转动频率为1.2 Hz。水平振动时域分析和谱分析分别如图7,8 所示。根据自谱图形,得到各测点自谱分析波形峰值及频率。水平振动自谱分析峰值如表3 所示。

表3 水平振动自谱分析峰值Tab.3 Spectrum analysis peak of horizontal vibration

图7 水平振动时域分析Fig.7 Time domain analysis of horizontal vibration
由图7 可知:各测点振动反应由于所处位置不同而不同,同一测点南北向和东西向峰值没有同步出现,说明结构南北向和东西向的自振特性不同,与2.2 节中扭转测试结果吻合。
由图8 可知:0.74 Hz 时各测点横向振动反应曲线均出现第1 个谱幅值;0.80 Hz 时各测点纵向振动反应曲线均出现第1 个谱幅值;1.18 Hz 时各测点纵向振动反应曲线均出现第2 个谱幅值,且为各测点的纵向最大位移幅值,其主要原因是该频率与风机转动频率接近,说明采样频率受风机转动影响较大。根据自谱分析结果,并考虑现场风机转动对试验结果的影响,确定结构第1 阶频率为0.74 Hz,第2阶频率为0.80 Hz,第3 阶频率为1.18 Hz。
由表3 可知:柱底测点5 纵横向位移在2.08×10-4~8.28×10-5mm;柱中测点4 纵横向位移在0.004 0~0.016 4 mm,与测点5 相比,位移增加最大约为94%;柱顶测点3 纵横向位移在0.015 0~0.049 7 mm,与测点4 相比,位移增加最大约为206%;钢桁架顶测点2 纵横向位移在0.011 2~0.051 2 mm,与测点3 相比,位移增加最大约为11%;A 型架顶测点1 纵横向位移在0.013 8~0.052 3 mm,与测点2 相比,位移增加最大约为2%。因此可见,测点位移随着点布置高度增加而呈现不同程度的增加,最大位移发生在A 型架顶,其值为0.052 3 mm。
根据同一固有频率处各测点振幅谱图的峰值可确定出固有振型幅值的相对大小,图9 为实测振型图。由图可知,结构前2 阶实测振型接近,表明结构可能不以某一阶振型为主,而存在振型耦合。结构下部的相对变形大于上部,在柱顶(32.0 m)以上的钢桁架和A 型架刚度较大,相对变形较小。A 形架的振动有回收趋势,表明结构的竖向质量和刚度在A 形架处发生了突变。

图9 实测振型(单位:m)Fig.9 Tested vibration mode(unit:m)
5 结构模态分析
5.1 模型构建
利用ANSYS 有限元软件对上节中的试验结构建立有限元计算模型,如图10 所示。该模型采用Beam188 模拟结构钢桁架等线形构件,上部A 型架、挡风墙和风机以质量形式用Mass21 单元加在空冷平台上部的节点上,用Shell63 模拟A 型架上主要设备的质量和对结构刚度的贡献,采用了与文献[2-3]类似的组合截面模拟方法模拟钢筋混凝土管柱,管柱与钢桁架以铰接连接,在模型中柱底端施加位移全约束,即6 个自由度。采用理想弹塑性材料模型模拟钢材力 学性能,Sargin 和Saenz 模型[4-5]模拟混凝土应力与应变关系。
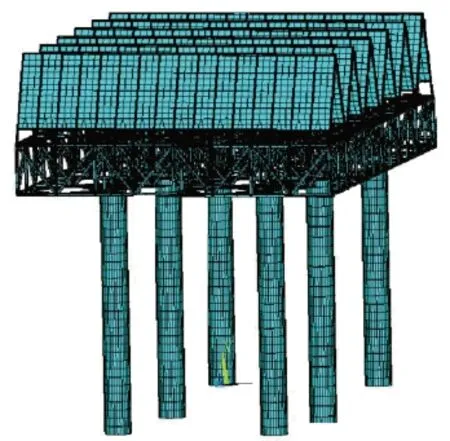
图10 有限元模型Fig.10 Finite element model
5.2 模态分析
结构有限元模型建立后,采用高精度的模态分析方法Subspace 提取结构的前几阶振型和频率进行分析。计算振型如图11 所示。表4 为计算分析得到的前3 阶频率以及与上节实测所得频率的比较。

表4 频率比较Tab.4 Frequency comparison
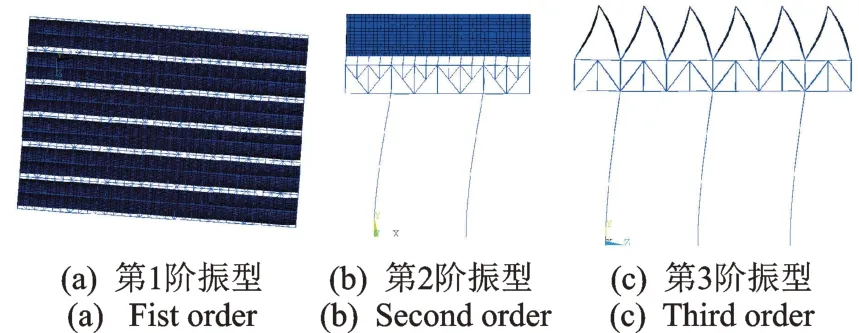
图11 计算振型Fig.11 Calculated vibration modes
图11 所示的振动形态表明,计算模型第1 阶为扭转振型,第2 阶为南北方向平动振型,第3 阶为东西方向平动振型,第3 阶以后的振型为风机桥架和局部杆件的振动。根据2.2 节和4.2 节中的实测结果,结构实测振型1 阶为扭转、2 阶为南北方向平动、3 阶为东西方向平动,表明计算振型与实测结果吻合。根据表4 中频率对比情况,计算所得频率和实测所得频率吻合较好,但计算频率小于实测频率,主要是因为计算模型对柱节点、A 型架上排气管道、蒸汽分配管、圆管以及结构上部的检修平台隔墙、门、步道、栏杆、连接件等局部构造和非承重构件进行了简化处理,导致了模型刚度降低。
综合以上分析结果,计算模态与实测振型相吻合,二者频率接近,说明计算模型能较好地反映实际结构的自振性能,可进一步为结构动力荷载(风机扰动、地震及风荷载)等动力响应研究提供依据。结构低阶振型接近,存在耦合,不能采用底部剪力法计算该类结构地震作用。常规民用建筑中不常出现1 阶扭转,该结构1 阶为扭转振型,不利于结构抗震,必须重视该类结构的抗扭问题。高阶振型中表现出局部杆件和风机桥架振动,由于结构为大跨长悬挑结构,设计时应考虑竖向地震影响。
6 结 论
1) 各测点振动波形由于所处位置的不同而不同。同一测点南北向和东西向峰值出现时刻不同,说明结构南北向和东西向的自振特性不同。中间测点反应比角部测点反应小,表明结构存在扭转。
2) 前2 阶振型接近,说明结构可能不以某一阶振型为主,而存在振型耦合。结构下部管柱的相对变形大于上部钢桁架和A 型架的变形,A 形架振动呈现回收趋势,表明质量和刚度在该处发生了突变。
3) 有限元分析模态与实测振型吻合,频率接近,说明模拟结果能较好地反映出实际自振性能,可为研究结构动荷载响应提供依据。结构低阶振型接近,不适合采用底部剪力法计算地震作用。

