基于功率谱的美声发声特征提取∗
张 凯, 王舒蕾, 齐婷婷, 张义民
(1.沈阳化工大学装备可靠性研究所 沈阳,110042) (2.沈阳音乐学院戏剧影视学院 沈阳,110818)
引 言
美声唱法由于音色清脆高亢、灵活多变及音量较大[1],对于歌唱者的发声技巧要求较多,且美声唱法的共鸣是“所有腔体共同运作达到整体效果的展现”。相比于其他唱法,美声唱法需要共鸣腔体以及骨骼都参与共鸣,即要求身体的各个器官放在一起共同产生共鸣。其他唱法参与共鸣的器官相对较少,发声的位置也有所不同[2],导致美声初学者在头腔、口腔、胸腔和咬字等方式上相对于其他唱法出现的问题较多。目前,在声乐领域的教学中,基本是通过老师的言传身教来纠正学生歌唱技巧上的错误。为了更深入研究美声发声的特点,笔者利用美声发声信号的功率谱去评价初学者的发音状态,从振动理论的角度比较发音的异同,从功率谱中提取美声发声的信号特征。
国内外学者围绕美声发声原理开展了相关研究。文献[3-5]从声门振动和空气动力学的角度对声音信号进行了分析。Mayr[6]利用长期平均频谱(long-term average spectrum,简称LTAS)和功率谱对美声男高音的生理和声学特征进行了研究,比较了假音和胸腔音的差异。Souza[7]通过对女高音的共振峰分析比较,得到音高的变化会导致基频和共振峰的不同。Hasan 等[8]使用经验模态分解(empirical mode decomposition,简称EMD)方法对歌曲的清音和浊音进行能量估计,以观察学习者歌声中的差异和错误。Zysk 等[9]设计了一套声音记录程序,利用频谱特征对女高音的头部和胸部音域表演进行分类。Barlow 等[10]根据平均元音谱(average vowel spectra,简称AVS)和长期平均谱对歌手在古典和现代风格之间的声乐作品的差异进行了量化。
国内学者的研究主要集中在美声唱法与民族唱法、流行唱法的融合与对比领域[11-13],但针对声音信号特点进行研究的文献较少。钱一凡等[14]针对标准元音提取了其基频、共振峰和各通道振幅,比较不同元音的声学特征,分析得知不同的元音发声与身体不同部位的共鸣有关。
大部分关于发声信号的研究采用傅里叶变换的方法,将原时域信号转化为频域信号。然而,频域信号仅对变换后信号的实部进行对比,忽略了相频信息。另外,对美声唱法样本的采集主要集中在美声与通俗唱法的对比上,但是通俗唱法从发声特点上与美声唱法存在明显差异,难以突出美声声音信号的特殊性。
针对上述问题,笔者利用功率谱的估计对信号进行研究,即从能量的观点对信号进行分析,保留频谱法所丢掉的相位信息。同时,从美声初学者与歌唱技巧成熟的美声老师中提取样本并进行对比研究。因为美声初学者的发音近似美声,所以更适合对美声发音的规范性进行系统评价。
1 基于功率谱发声信号特征提取步骤
笔者对美声声音信号的特征提取主要分为以下步骤:①对声音信号进行采集;②对采集到的声音信号进行端点检测处理,去除无用的语音段;③对处理后的信号做Burg 法功率谱分析;④将得到的功率谱进行局部二次回归平滑处理。
1.1 声音信号样本的采集与端点检测
对5 名美声初学者和3 名美声老师进行女高音信号的采集、筛选和分类。录音时要求发音人在相同录音环境下依次清唱出基础元音/a/,/i/和/u/,在录制的声音样本中选取发声时长在3~5 s 的语音信号,最终得到老师的发音样本50 条(设定为正确发声信号)和学生的错误发音样本350 条。美声老师分别对学生的样本进行错误分析,指出发声存在的问题,总结出“口腔没打开”、“咬字位置不正确”等一系列错误原因。为了便于分析,下面只讨论发声为/a/的分析结果,并不影响其统计规律。
由于采集到的美声信号中存在无效的静音段和噪声段,会对功率谱分析和特征提取存在一定程度的干扰,增加运算量,因此需要对声音信号进行端点检测,确定其起点和终点,以便提高计算效率。笔者采用一种基于短时能量和谱质心特征进行端点检测的方法[15],其方法步骤如下。
首先,对语音信号中的每一帧提取短时能量,设xi(n)(n=1~N)为第i帧信号,长度为N,该帧的能量E(i)为
其次,提取该帧的谱质心。设第i帧的谱质心Ci为
其中:Xi(k)(k=1~N)为第i帧的离散傅里叶变换;N为帧长度。
最后,估计短时能量和谱质心特征序列的阈值,设M1和M2分别为2 个局部最大值的位置,则阈值T为
其中:W为笔者设置的参数,W越大,阈值就越靠近M1。
经过上述阈值化处理,可以得到一段标记语音段的阈值化序列,将该序列代入原始信号中,就可获得语音段在原始信号中开始和结束的位置。
1.2 Burg 法功率谱估计
将完成端点检测的信号进行Burg 法功率谱分析。在对随机信号的分析中,可以利用自回归(autoregressive model,简称AR)模型进行功率谱估计。其中,Burg 法无需对自相关函数进行估算,而是用已知序列x(n)求出反射系数,再利用Levinson 递推算法,由反射系数来计算回归模型参数,以得到较好的谱估计结果。
利用Burg 法估计AR 模型参数,首先要确定式(4)所示的初始条件,其次根据序列x(n)求出式(5)所示的自相关函数σ20
令k=1,计算AR 模型的反射系数Kk
在Levinson 关系式的ak(i)(i=1~k-1)中,分别代入p阶AR 模型反射系数和p-1 阶AR 模型反射系数,计算aki(i=1~k-1)、前向预测误差ek(n)和后向预测误差bk(n),分别为
根 据计 算 出σ2k,令k=k+1。重复上述步骤,直至预计的阶数为止,以求出所有阶的AR 模型参数。
Burg 估计算法的递推过程建立在已知序列的基础上,很好地避免了对于序列自相关函数的计算,与其他算法相比,有着较好的频率分辨率[16]。
1.3 局部二次回归平滑
笔者使用局部二次回归平滑对Burg 法得到的功率谱进行平滑处理。局部二次回归平滑就是使用二次多项式作为局部多项式的回归拟合,是一种用于局部回归分析的非参数方法。
在对信号进行二次回归平滑时,首先要确定拟合点的数量和位置,再以拟合点为中心,确定k个最邻近的点,通过权重函数计算这些点的权重。其中,对权重的计算要先确定区间内的点到拟合点的x轴的距离,找到区间内的最大值,然后对其他距离做归一化处理。归一化函数表达式为
使用三次指数函数对权重进行转化,三次函数表达式为
接下来对区间内的散点进行局部二次回归拟合,考虑到离拟合点的远近不同,点的取值对拟合线的影响也不同,故在定义损失函数时,应率先降低近的点与拟合线的误差,即对最小二乘法加上权重。加权最小二乘法的表达式为
对区间内的样本进行多项式拟合后,不断重复拟合过程,得到不同区间内的加权回归曲线,最后通过对回归曲线中心的连接,便可生成完整的平滑曲线。
1.4 BP 神经网络
笔者选取BP 神经网络用于美声特征的分类。BP 神经网络作为一种多层的前馈神经网络,由输入层、隐藏层和输出层组成。本研究对BP 神经网络设置2 个隐藏层:第1 个隐藏层包含10 个神经元,使用线性函数作为激活函数;第2 个隐藏层包含2 个神经元,使用对数S 形转移函数作为激活函数。所选样本数据为平滑处理后的信号功率谱特征值,最后选择梯度下降自适应学习率的反向传播算法作为训练函数来训练BP 神经网络。
2 实验数据采集与分析
采集某音乐学院5 名女高音新生和3 名老师的美声发声信号共400 条,利用Matlab 软件对经过预处理的美声信号进行Burg 功率谱估计,对比正确样本与错误样本之间功率谱形态走势的区别,对与正确功率谱图像差距较大的地方做函数图像的拟合,并提取谱图的特征参数,最后比较科学美声发声和错误美声发声之间功率谱曲线与参数的差距。
2.1 信号的Burg 功率谱估计
声音信号端点检测时域波形如图1 所示。首先对采集到的美声信号进行端点检测,原始信号的时域波形见图1(a),去除多余的静音段和噪声段,得到无干扰的声信号时域波形见图1(b)。

图1 声音信号端点检测时域波形Fig.1 Time domain waveform of sound signal endpoint detection
将预处理后的信号带入25 阶AR 模型,美声发声信号功率谱曲线如图2 所示,得到正确美声信号功率谱和3 种具有代表性的、不同错误类型的美声信号功率谱。根据图中功率谱整体的波动和走势情况,可将功率谱划分为3 个能量区,如图2 中竖线所示。其中:0~6 kHz 为第1 能量区;6~11 kHz 为第2能量区;11~15 kHz 为第3 能量区。

图2 美声发声信号功率谱曲线Fig.2 Power spectrum curve of bel canto signal
由功率谱曲线可以看出,高音信号的功率谱整体均呈下降趋势。由图2(a)的标准美声信号功率谱中可以发现,1,6 和15 kHz 处均存在明显的峰值变化,6 kHz 处有明显的下降趋势,波谷平均深度为-100 dB,与波峰有着40 dB 的落差。曲线从10 kHz开始平稳下降且无较大波动,在15 kHz 处下降速度加快,曲线陡峭,至17 kHz 处降至最低点-140 dB。
在错误美声信号的功率谱中,图2(b)所示的错误样本1 存在着“口腔没有打开、气息没有用上”的错误,其功率谱在6 kHz 处的波谷相对较浅,与左侧波峰的落差仅有20 dB,而在15 kHz 处的曲线呈明显上升趋势的波动,持续约1 kHz 后加速下降至最低点。由图2(c)所示的错误样本2 可以看出,曲线在1,6 和11 kHz 处均有波谷产生,且波动幅度较大,曲线相对不稳定,存在“咬字位置不对”的错误,在15 kHz 处变陡加速下降。由图2(d)所示的错误样本3 可以看出,曲线整体无较大波动,几乎呈平稳态势下降,直至15 kHz 处曲线变陡并下降至最低点,存在“口腔发声位置错误”的问题。
从能量区的分割上可以看出,错误样本曲线在每个能量区中均有不同幅度的波动;而正确样本曲线只有在进入第2 能量区后有一处波谷,从第2 能量区中部至第3 能量区结束之间的图像下降匀速,无明显起伏特征。
2.2 信号的曲线拟合与箱式图
基于上述情况,笔者在功率谱曲线区别较大的区间内进行基于最小二乘法的一阶拟合和二阶拟合,得到一元二次曲线方程和一元一次直线方程,再对2 种方程的系数取平均值和方差。其中,一元二次方程拟合了3~7 kHz 之间功率谱中存在的波谷曲线,由于2 种信号在其区间内的变化差距较大,得到的方程在系数上有着较大差别。功率谱曲线一元二次方程拟合系数如表1 所示,正确发声信号曲线的一次项系数b大于错误信号,而二次项系数a和常数项c则小于错误信号。

表1 功率谱曲线一元二次方程拟合系数Tab.1 Fitting coefficient of the power spectrum curve by the quadratic equation
在曲线方程中,二次项系数a代表函数抛物线的开口大小,a的绝对值越大,抛物线的开口越窄。对于2 条抛物线A1x2+B1x+C1y+D1=0 和A2x2+B2x+C2y+D2=0,其开度公式分别为
将正确信号和错误信号的多项式系数分别代入σ1和σ2,得到σ1>σ2,即正确信号抛物线的开口度要大于错误信号。
再对图中10~15 kHz 的下降直线进行拟合,得到了斜截式的一次函数直线方程,功率谱曲线一元一次方程拟合系数如表2 所示。可以发现,正确信号的斜率k要小于错误信号,而截距b大于错误信号,即正确信号的倾斜坡度较大,错误信号坡度较为平缓。

表2 功率谱曲线一元一次方程拟合系数Tab.2 Fitting coefficient of power spectrum curve by linear equation
为了更直观地观察数据的离散分布情况,了解数据分布状态,将拟合出的多项式系数进行箱式图分析,如图3 所示。由图3(a)所示的二次项系数a的箱式图可以看出:错误信号的系数整体低于正确信号,其箱式图长度较短,数据多集中分布在很小的范围内;正确信号的箱式图较长,表明数据间差异比较大,方差也大于错误信号。由图3(b)所示的斜率k的箱式图可以看出:正确信号的数据波动较大,但在错误信号中存在一处离群值,导致方差比正确信号的方差大。
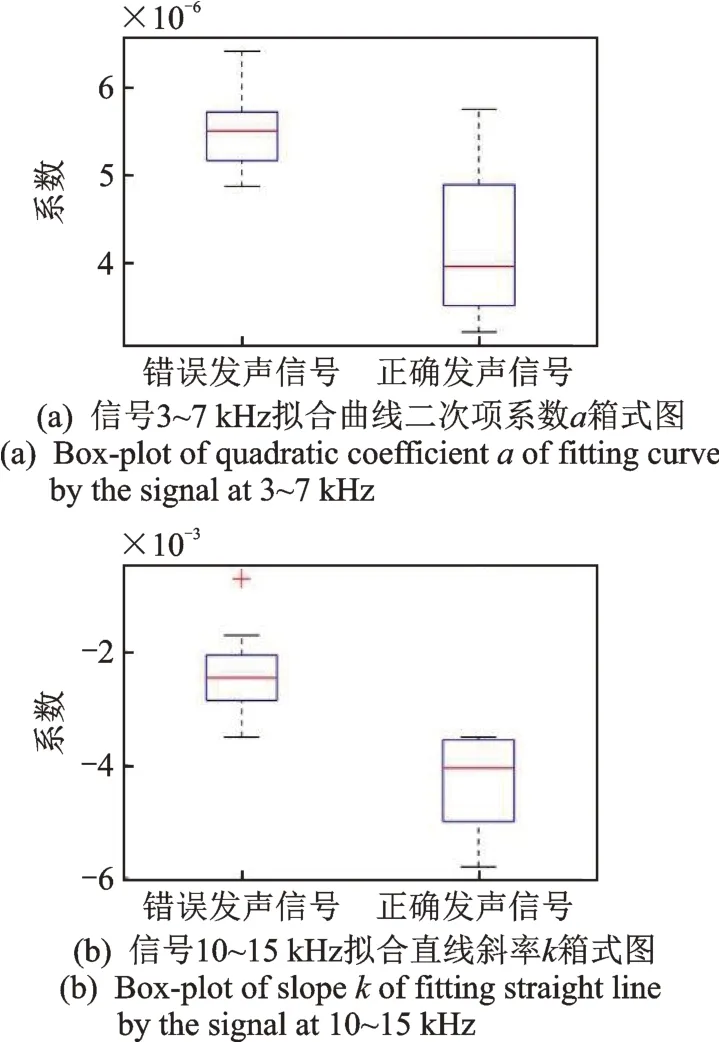
图3 多项式系数箱式图Fig.3 Box-plot with polynomial coefficients
由箱式图可知,在二次项系数箱式图的5×10-6处和斜率箱式图的-3×10-3处均有明显的分界,可以把正确信号和错误信号按照分界数值直接区分开,故采用阈值法的识别率可达到100%。
对美声信号的功率谱曲线做特征值统计,如表3 所示。由表可知,错误信号的方差明显大于正确信号,说明错误信号的功率谱数据波动较大,数据分布比较分散,在平均数附近波动较大,且存在较大的上下限差。

表3 美声信号功率谱统计特征值Tab.3 Statistical eigenvalues of power spectrum of bel canto signal
2.3 基于BP 网络的神经分类
对400 条声音信号进行训练集和测试集的划分,其中75%的数据作为训练集导入BP 神经网络中进行训练,使BP 神经对两类发声信号的特征值有记忆能力;再将剩余的15%数据作为测试集,来测试BP 神经网络的识别正确率。BP 神经网络收敛图如图4 所示,由图可以看出,训练在120 次左右达到收敛,识别率为95.23%。

图4 BP 神经网络收敛图Fig.4 Convergence diagram of BP neural network
由BP 神经网络的识别结果可知,相比于利用BP 神经网络对美声进行分类,基于系数箱式图的阈值法可以更直接地将2 种类别区分开,且识别率达100%。因此,采用函数拟合的方法明显优于直接对功率谱特征值进行分类训练的方法。
3 结 论
1) 标准美声唱法的功率谱仅在6 kHz 左右有一处明显的波谷,下降落差约为40 dB,其余频率并无较大的波谷产生。在错误的美声唱法中,有些谱线没有明显的波谷,而有些谱线波谷较多,波动幅度较大。对3~7 kHz 内的波谷曲线和10~15 kHz 内的下降直线分别做一元二次函数拟合和一元一次函数拟合,可以得出正确信号在拟合的曲线上有着更大的开口度和更深的波谷,在直线上有着更大的倾斜度。在系数箱式图中使用阈值法,可以将2 种类型的信号直接区分开。
2) 根据功率谱的波动和走势,可将其划分为3个能量区。在能量区中,错误样本的曲线波动频率更大,且在区域交界处有波谷;正确样本仅在第1、第2 能量区之间有波动,其余区域波动较不明显。
3) 使用美声声音信号功率谱进行2 种声音信号的BP 神经网络训练和分类识别,识别正确率可达95.23%;而使用系数阈值法,可实现对2 种发声信号的100%分类,表明本研究提出的美声发声信号特征阈值法更加有效。
4) 可以利用笔者目前的研究结果建立一套针对美声发声的打分系统,用于评估声乐初学者在发声训练时的标准程度。

