基于SGHT 的航天器微振动信号处理方法∗
陈继喆, 章海鹰
(1.中国科学院国家天文台南京天文光学技术研究所 南京,210042)
(2.中国科学院天文光学技术重点实验室(南京天文光学技术研究所) 南京,210042)
(3.中国科学院大学 北京,100049)
(4.中国科学院大学天文与空间科学学院 北京,100049)
引 言
航天器飞轮微振动是影响空间光学载荷成像质量的主要因素[1]。为了评估微振动的影响,在研制阶段需要开展地面微振动试验[2]。常见的试验方法是多点布置压电振动传感器,采集飞轮工作时不同位置的加速度信号。这种方法测量难度低,且可以对航天器内部进行测量,但得到的航天器微振动加速度信号需要进一步处理[3]。
通常情况下,希望经过处理后的微振动信号提供两方面的信息:①频域上分析微振动能量集中的特定频段,指导载荷结构优化以避免与飞轮微振动发生共振;②时域上通过对微振动加速度信号二次积分,得到微振动线位移、角位移估计,判断平台扰动对光学成像的具体影响。因此,研究如何处理航天器微振动信号是开展地面微振动试验的必要保障。
为得到频域信息,考虑微振动信号的非平稳特性,可以采用希尔伯特-黄转换(Hilbert-Huang transform,简称HHT)进行处理,即将原始信号经过经验模态分解(empirical mode decomposition,简称EMD)处理后,对各信号分量通过希尔伯特转换(Hilbert transform,简称HT)求解瞬时频率,绘制时间-频率-瞬时能量瀑布图,得到包含频域能量分布特征的边际谱。这种信号处理方法简单,但缺点是EMD分解过程中容易产生欠包络、过包络和频率混淆等问题,导致得到的频率成分可能在实际信号中并不存在,从而影响对微振动特征的识别。
为得到时域信息,常见的方法包括频域积分法和时域积分法。频域积分法通过快速傅里叶变换(fast Fourier transform,简称FFT)在频域实现加速度与位移的相互转换[4];时域积分法通过例如辛普森公式的数值积分方法,直接对时域加速度信号进行积分。这两种方法都可以得到时域位移数据,但都存在低频段微小噪声和误差引发二次积分后位移出现巨大趋势偏差的问题。为了消减趋势偏差影响,目前有多种常用方法可以对加速度信号和积分位移进行处理。
从加速度信号入手,考虑到低频段噪声误差是引起位移趋势偏差的主要原因,高通滤波算法[5]和低频衰减滤波算法[6]选择舍去部分低频段加速度信号特征,对趋势偏差有一定改善,但需要根据工程经验设置低频参数,且没有消除通带内信号的噪声,噪声鲁棒性较差。小波积分方法尽管曾用于处理量子科学实验卫星的微振动加速度信号[3],但同样需要选择恰当的窗函数构建衰减曲线[7],也存在低频衰减算法的众多缺点。
从积分位移入手,位移的长周期趋势项是趋势偏差的主要构成。多项式去趋势方法通过对积分位移进行多项式拟合,将拟合的多项式剔除以去除趋势项。该方法主要针对因为初值不确定产生的趋势项误差,对其他原因产生的趋势项误差拟合效果较差。EMD 方法分解得到的最长周期残余信号通常可以代表原信号的趋势或均值,因此也可以用于信号的去趋势处理[8],但实际工程中受限于分解能力,效果并不理想。
针对现有常用航天器微振动信号处理方法的不足,笔者提出SGHT 方法,自适应地完成频域特征获取及时域信号处理。首先,对输入的时域信号进行SGMD[9-10],得到各信号分量,具有良好的噪声鲁棒性和分解性能;其次,引入归一化互信息作为评价指标,同时参考迭代式SGMD 方法[11],迭代式的输出单信号分量归类重组的SGC,进一步增强自适应能力、噪声鲁棒性和分解性能;最后,应用希尔伯特谱分析,得到各信号分量的瞬时频率,并以频域能量分布的形式输出结果。
在频域特征获取方面,SGHT 方法将微振动加速度信号作为原始输入信号,可以在有噪声干扰的情况下,分解、重构信号并输出各SGC 分量及对应的频谱特征,对于常用HHT 方法难以处理的含噪非平稳微振动信号,SGHT 方法具有显著优势。
在时域信息处理方面,首先,使用SGHT 方法处理微振动加速度信号;其次,对处理后的微振动加速度信号二次积分,得到微振动位移估计;然后,将得到的位移估计作为输入信号再次进行SGHT 处理,得到各SGC 分量及对应的频谱特征;最后,将包含趋势项的SGC 分量去除,得到更准确的二次积分位移结果。
1 基本原理
本研究辛几何-希尔伯特的转换流程见图1。
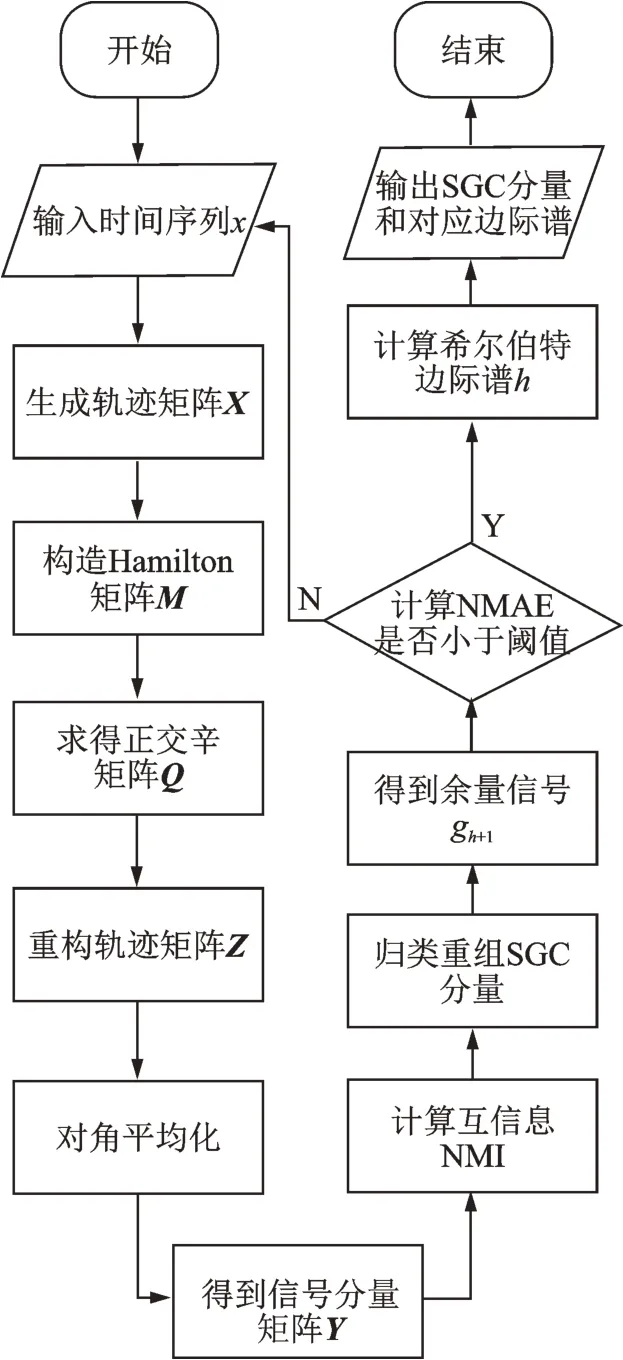
图1 辛几何-希尔伯特的转换流程Fig.1 The process of SGHT
1.1 相空间重构
设输入的原始信号时间序列为x=x1,x2,…,xn,其中n为数据长度,重构序列可以得到轨迹矩阵X为
其中:d为嵌入维数;τ为延迟时间,可取1;m=n-(d-1)τ。
嵌入维数用功率谱密度法确定[12],首先计算信号时间序列x的功率谱密度(power spectral density,简称PSD),然后估计PSD 中最大峰值对应的频率fmax,嵌入维数即确定为,其中Fs为 输入信号的采样频率。为缩小计算规模,嵌入维数最大限定为200。
1.2 辛几何矩阵变换
令协方差对称矩阵A=XTX,构造Hamilton 矩阵M为
令矩阵N=M2,则N也为Hamilton 矩阵。构造正交辛矩阵Q
其中:Q为正交辛矩阵,在变换后依然保留Hamilton矩阵的结构形式;B为上三角矩阵,即矩阵元素bij=0(i>j+1)。
矩阵B可通过对矩阵N施密特正交化得到,其特 征 值 为λ1,λ2,…,λd。根 据Hamilton 矩 阵 的 性 质可知,矩阵A的特征值σi=(i=1,2,…,d),设Vi(i=1,2,…,d)为矩阵A对应于特征值σi的特征向量。
计算转换系数矩阵Si=ViTXT,得到重构矩阵Zi=ViSi,Zi(i=1,2,…,d)即为初始单分量矩阵。重构轨迹矩阵Z由d个组分组成,可写为Z=Z1+Z2+…+Zd。
1.3 对角平均化
实际得到的重构轨迹矩阵Zi为m×d矩阵,为了得到长度为n的时间序列,需要对其进行对角平均化。对于任一初始单分量矩阵Zi,定义矩阵的各元 素 为zij,其 中:1 ≤i≤d;1 ≤j≤m。 令d*=min (m,d),m*=max (m,d),n=m+(d-1)τ。当m 由式(4)计算得到的y1,y2,…,yn即为对Zi处理得到的一组长度为n的一维时间序列Yi。对各重构轨迹矩阵Zi依次处理,可得到原信号分解的d组长度为n的分量,即原信号x=Y=Y1+Y2+…+Yd。 矩阵分解得到d个单分量信号后,并非每个单分量都是独立分量,多个不同分量可能由相同的原因引起扰振,具备相似的特征。因此,本方法将归一化 互 信 息(normalized mutual information, 简 称NMI)作为评价指标,将NMI 较高的分量归类重组。同时,测得的原始信号可能还包括测量误差和其他因素引起的噪声,这些分量不宜归类重组,需要设置合适的终止条件。 计算Y1与其他分量的归一化互信息,即 其 中:EB(A)=-∑a P(a)logP(a),为 边 界 熵;EJ(X,Y)=-∑x∑y P(x,y)logP(x,y),为联合熵。 若存在其他分量与Y1的归一化互信息高于设定的阈值,则所有符合阈值条件的分量与Y1归类重组为SGC 分量;若不存在此条件分量,则Y1单独组成SGC 分量。 在原始信号中去除得到的SGC 分量,得到余量信号gh+1(t)为 计算所得残余项和原信号之间的归一化平均绝对 误 差(normalized mean absolute error, 简 称NMAE),即 其中:gh+1(i),x(i)分别为gh+1(t),x(t)时程的位移采样值;Npoint为信号的时间采样点数。 NMAE 作为归一化指标,其最大值为残余项信号且是原信号自身时,则NMAE 为1;其最小值为不存在残余项信号时,则NMAE 为0。因此,根据此范围可以将NMAE 的默认阈值确定为0.1。 当NMAE 小于给定阈值即代表原始信号已经完成分解;否则得到的余量信号将作为新一轮分解过程的输入信号,并分解得到新的SGC 分量。 对处理后的SGC 分量进行希尔伯特变换,即 构造解析函数 其中:ai(t)为包络信号;θi(t)为瞬时相位;ωi(t)为瞬时角频率。 该信号的希尔伯特谱可表示为 希尔伯特边际谱表示为 希尔伯特边际谱幅值是每一个频率点幅值在时间全局上的积分[13],从统计学角度看,幅值越大表示具有该频率的特征分量在整个信号持续时间内某一时刻出现的可能性较高,因此能够精确反映某一频率是否真实存在[14],其幅值是适合定性分析的无量纲量。最终,输出所有SGC 分量及其对应的希尔伯特边际谱。 为了模拟实际信号在频谱中呈现“枞”状分布的特性,在现有航天器飞轮微振动模型[15]的基础上,假定飞轮转动过程中转速和幅值变化的瞬态效应不可忽略,但其在微小时间段(1 个谐波周期)内仍保持常数。因此,在原线性稳态模型中引入变化因子,微振动模型可表示为 其中:a(t)为加速度;n为模型总阶数;Ci为第i阶谐波的振幅系数;frwa为飞轮转速频率;αij和βij分别为控制幅值和周期的随机变化因子;j为第j个谐波周期;hi为谐波级次;t为时间;φi为[0,2π]区间内的随机相位。 微振动模型的优点在于可以根据公式积分推导出加速度模型所对应的理论位移,便于对仿真信号积分处理后的结果进行验证。 参考微振动信号特性[15]和其他现有微振动模型参数[16],微振动模型参数体现如下:各阶谐波级次呈倍数递增,一般低阶谐波级次振幅较大,是微振动信号中的主导;高阶谐波级次振幅较小,通常可以认为前几阶谐波级次生成的信号足以反映微振动信号特性。因此,选用3 阶谐波级次用于生成仿真信号,设定变化因子αij和βij在[0.75,1.25]区间内随机,其他微振动模型信号生成参数如表1所示。 表1 微振动模型信号生成参数Tab.1 Signal generation parameters of micro-vibration model 根据式(15)和表1,生成不同飞轮转速下的微振动加速度仿真信号。模拟飞轮转速为2 kr/min 时的微振动加速度仿真信号如图2 所示,其中:a1,a2,a3为仿真信号各成分;asum为总的仿真信号。 图2 飞轮转速为2 kr/min 时的微振动加速度仿真信号(1~1.5 s)Fig.2 Simulation signal of micro-vibration acceleration at flywheel speed of 2 kr/min (1~1.5 s) 以2.1节生成的模拟飞轮转速为2 kr/min时的微振动加速度仿真信号为对象,加入信噪比为10 dB 的高斯白噪声,验证本研究SGHT 方法的频谱特征获取能力,同时选取HHT 方法进行对比。为抑制HHT 和SGHT 方法处理后端点效应的影响,HHT和SGHT 方法的输入均经过极值对称延拓方法[17]预处理。 使用HHT 方法对预处理信号的处理结果如图3 所示。 图3 HHT 方法对预处理信号的处理结果Fig.3 Processing results of simulation signal by HHT HHT 方法的主要思路是:先对输入信号进行EMD 分解,再对分解得到的本征模函数(intrinstic mode function, 简称IMF)分量做希尔伯特转换,得到信号分量的瞬时频率。因为本研究更加关注频域上微振动能量的整体分布特征,所以选用希尔伯特边际谱。 由图3 可以看出,HHT 方法难以对仿真信号进行分解,其边际谱中可辨别的频率峰值出现在了11,19,23,58 和63 Hz,其中只有23 Hz 的信号分量与仿真信号某成分特征相符,其他信号分量均不同程度出现了模态混淆现象,得到的频谱特征结果无法反映输入信号的基本特征。 使用SGHT 方法对预处理信号的处理结果如图4 所示。 图4 SGHT 方法对预处理信号的处理结果Fig.4 Processing results of simulation signal by SGHT 由图4 可以看出,SGHT 方法能够准确地对输入信号进行分离、降噪及识别,得到特征频率分别为26,58 和84 Hz 的信号分量,同时分离得到的各SGC 分量与混合前的各信号成分基本相符,可反映原始信号成分的物理意义。与HHT 方法相比,SGHT 方法在降噪和分解方面具有显著优势,能够有效处理微振动加速度仿真信号,因此SGHT 算法在频域特征获取方面符合微振动信号处理要求。 同样以2.1节生成的模拟飞轮转速为2 kr/min 时的微振动加速度仿真信号为对象,加入信噪比为10 dB 的高斯白噪声,验证本研究SGHT 方法的时域信号处理能力,即根据加速度仿真信号处理得到线位移估计,并与工程常用处理方法进行对比。 用于对比的常见处理方法包括:加速度处理方法高通滤波;积分方法辛普森公式积分; 位移处理方法多项式去趋势和EMD。组合这3 种方法得到整体信号处理方法,同时还有整体处理信号的小波积分方法。高通滤波设置低频截止频率为10 Hz。小波积分参考文献[3]中的参数,设置最低截止频率为5 Hz,最高截止频率为500 Hz,窗函数为高斯窗(σ=10)。同时,为抑制EMD 和SGHT 方法处理后端点效应的影响,EMD 和SGHT 的输入经过极值对称延拓方法预处理。 对微振动加速度仿真信号采用选定的加速度处理方法、积分方法及位移处理方法进行处理,比较处理得到的线位移估计与微振动模型直接得到的理论位移,各方法得到的线位移估计误差结果如表2所示。 表2 各方法得到的线位移估计误差结果Tab.2 The error results of the estimated linear displacement processing by each method 表2 中,平均差值误差定义为线位移估计xest(t)与理论位移xideal(t)的差值在时程内的峰值相对于理论位移xideal(t)峰值的误差平均值,即 累计相对误差定义为线位移估计与理论位移差值绝对值的总和与理论位移绝对值总和的比值,即 其中:xest(i),xideal(i)分别为xest(t),xideal(t)时程的位移采样值;Npoint为信号的时间采样点数。 部分方法线位移估计与理想位移的绝对误差如图5 所示。 图5 部分方法线位移估计与理想位移的绝对误差(0~0.1 s)Fig.5 The absolute error between the estimated linear displacement and ideal displacement of partial methods(0~0.1 s) 由表2 和图5 可以看出:未处理的加速度信号在二次积分后,即便以多项式去趋势方法处理位移,得到的结果依然出现了较大的误差偏差,这是因为二次积分会放大未处理信号低频段的微小噪声,导致积分结果无法体现实际位移;高通滤波和小波积分针对这一问题,通过对低频段加速度信号的过滤和衰减,使积分误差降低至一定范围,但缺点是会损失低频段信号的部分有效信息;EMD 方法通过分解分离信号中的长周期趋势项,相较于多项式去趋势方法的简单拟合具有一定优势,但EMD 方法的处理结果受端点效应影响,造成两端的绝对误差较大;将SGHT 方法同时应用于加速度处理和位移处理,其能够在不损失低频段信号有效信息的基础上,对加速度信号中的噪声进行有效的处理,得到与理论误差最为接近的线位移估计结果。因此, SGHT 方法在时域信号处理方面符合微振动信号处理要求,可以有效得到线位移估计数据,且优于常用的其他方法。 使用SGHT 方法对ASO-S 卫星/ FMG 载荷地面微振动信号进行处理,结果如图6 所示。 图6 SGHT 方法对ASO-S/FMG 微振动信号的处理结果Fig.6 Processing results of ASO-S/FMG micro-vibration signal by SGHT 根据ASO-S 卫星微振动试验大纲,在FMG 载荷安装面上共布置4 个三轴线加速度传感器,负责记录飞轮不同转速工况下的微振动试验数据。在微振动试验结束后,使用SGHT 方法对各工况下4 个加速度传感器的3 个轴向加速度数据进行频域处理。其中四飞轮在2 kr/min 稳定转速工况下1 个加速度传感器的z方向经处理后的数据见图6。由图可以看出,SGHT 方法能够对实际微振动加速度信号进行有效的分离、降噪及识别,识别到特征频率分别为59,65 和345 Hz 的信号分量,其中能量较大的65 Hz信号分量的频率约为该工况飞轮转速的2 倍,是该测点的主要微振动来源。根据这些频谱信息,可以进一步指导载荷的结构设计,以避免在相应频率附近发生共振。 同时,为了判断平台扰动对光学成像的具体影响,需要根据试验测得的微振动加速度信号估计载荷安装面的角位移,即进行时域处理。首先,用SGHT 作为加速度处理方法,对各加速度传感器各轴向加速度数据进行处理;其次,用辛普森公式作为积分方法,对处理后的加速度信号进行二次积分;然后,再次用SGHT 方法作为位移处理方法,分离趋势项,得到各测点的微振动线位移估计;最后,用最小二乘法拟合各测点形成平面,得到测点安装面即载荷安装面的角位移估计。对四飞轮同时工作在2 kr/min 稳定转速工况的数据进行处理,经SGHT 方法处理得到的载荷安装面微振动角位移估计如图7 所示。由图可以看出,经SGHT 方法处理得到的该工况下载荷安装面微振动角位移估计均在0.015"以内,进一步分析角位移是以10 Hz 特征频率为主的周期信号,这一角位移估计可以作为载荷外部的平台扰动数据,进一步验证FMG 载荷稳像系统的摆镜控制算法,判断微振动平台扰动对载荷成像是否构成影响。 图7 经SGHT 方法处理得到的载荷安装面微振动角位移估计Fig.7 The estimated angular displacement of micro-vibration of payload surface processed by SGHT 通过对不同转速工况下的试验数据进行处理,所得到的角位移估计还可以用于确定载荷在轨工作时合适的飞轮转速工况,减小工况对载荷性能的影响。 1) 在频域特征获取方面,SGHT 方法可以在有噪声干扰的情况下,分解、重构信号并输出各信号分量及对应的频谱特征。 2) 在时域信息处理方面,使用SGHT 方法作为加速度和位移处理方法,能够得到较为准确的线位移估计结果。 3) 使 用SGHT 方法 处 理ASO-S 卫 星FMG 载荷的地面微振动试验信号,处理得到的频谱特征和角位移估计可以进一步指导载荷的研制工作。 4) SGHT 方法作为一种新兴信号处理方法,目前还存在计算规模大、易受端点效应影响等缺点,有待进一步研究和完善。1.4 单分量重构
1.5 边际谱计算
2 仿真验证
2.1 微振动模型


2.2 频谱特征获取的仿真验证

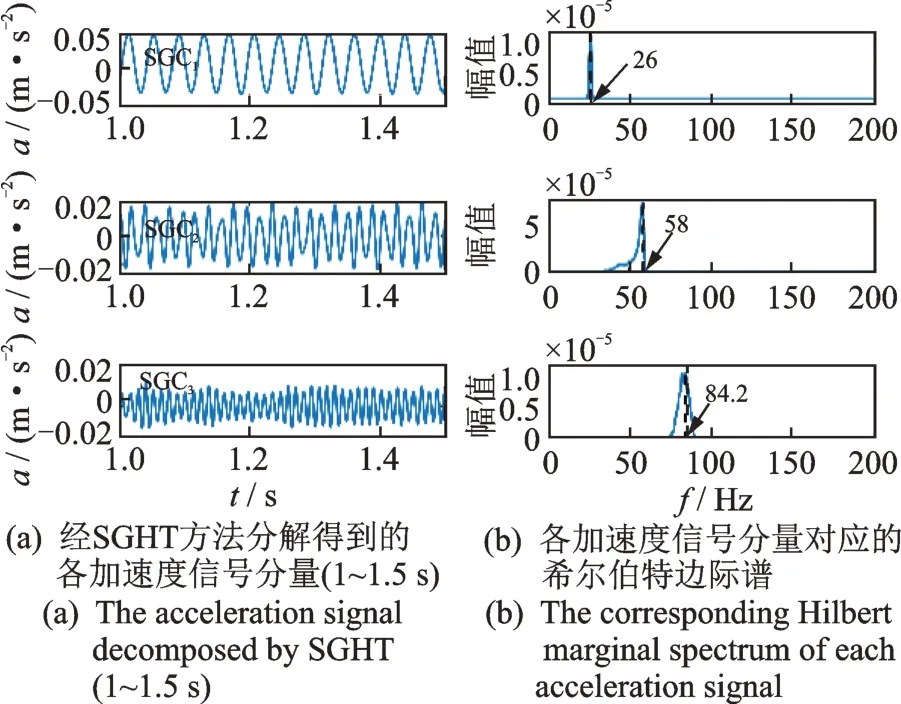
2.3 时域信号处理的仿真验证
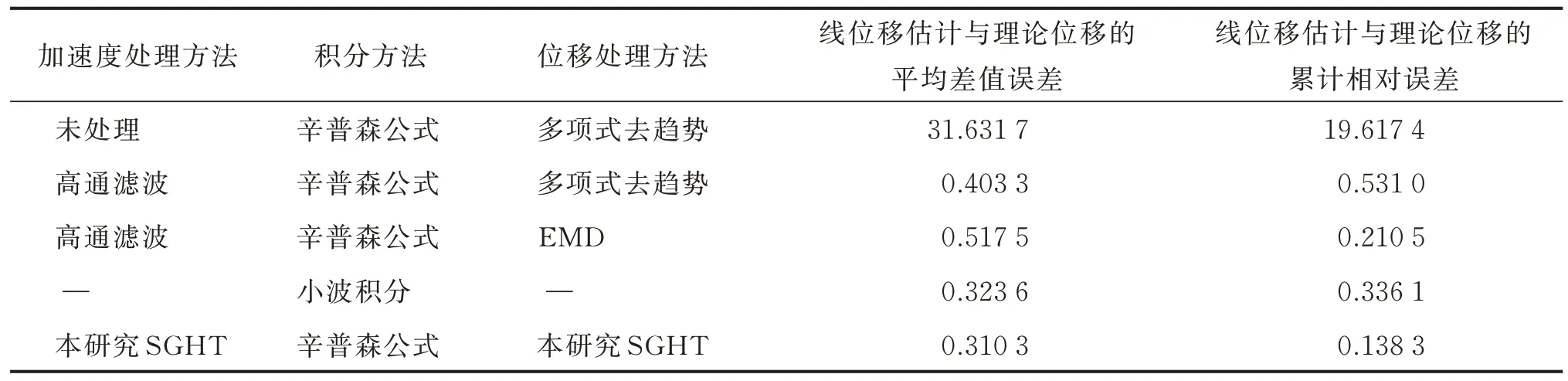
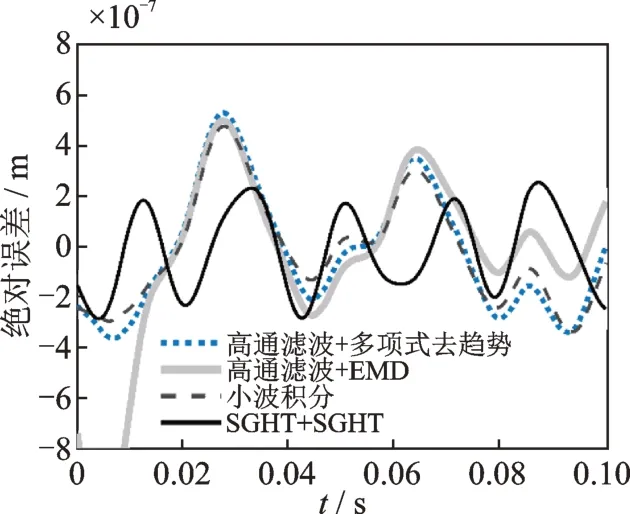
3 工程应用


4 结 论

