基于横向振动的旋转机械扭振信号提取方法∗
李启行, 谌 璨, 王维民, 李 帅
(1.北京化工大学高端压缩机及系统技术全国重点实验室 北京,100029)
(2.北京化工大学高端机械装备健康监控与自愈化北京市重点实验室 北京,100029)
引 言
随着我国对绿色环保、节能减排等方面越来越重视,特别是在“碳达峰”、“碳中和”概念提出之后,更为清洁、经济的电驱技术正在逐步取代传统的汽轮机和燃气轮机驱动。电动机驱动的优势在于变频驱动(variable frequency drive, 简称VFD),VFD 具有控制精确、调速平滑及调速范围大等特点[1]。但是,VFD 输出的正弦波动扭矩会引起转轴的扭转振动,VFD 同步电机中产生的波动扭矩会激发0~120 Hz 之间的所有固有频率[2]。大的扭矩波动会诱导快速升降的大扭转应力,且可能在机组启车过程中迅速发生[3],使人员和设备安全存在巨大的风险隐患。Feese 等[4]通过对使用VFD 的2 台不同的机组进行振动测试分析,发现其表现出相同的扭振行为,并证实了VFD 是扭振的激励源。风机在经过变频改造之后,出现了轴系损坏[5]、联轴器损坏[6]及扭转振动[7]等故障,经分析这些故障均是由VFD 引起的扭振所致。Kocur 等[8]分析了压缩机链中由VFD激发的电磁噪声对扭振的影响。
对运行中的机组进行扭振监测非常重要。扭振测量方式可分为接触式和非接触式两大类[9]。常见的扭振测量方式有应变测量[10]、齿盘或斑马带测量[11]及编码器测量[12]等。得益于传感器技术的发展和专门的扭振测试仪的研发,扭振的测量精度也在不断提高。张晓玲等[13]总结并分析了扭振测试中误差的成因,认为需要消除由横振带来的影响以改善扭振的测量精度,这是由于弯扭耦合现象的存在,弯曲振动对扭转振动有调频和调幅两方面的影响[14]。
扭转角的波动也会反映到横向振动上,因此笔者提出了一种基于横向振动传感器信号提取微弱扭转振动信息的方法,将调制在横向振动信号中的扭转振动信号解调还原为独立的扭振信号。采用该方法可避免安装齿盘、编码器等专门的扭振测试仪来对扭振信号进行监测,极大地利用横向振动传感器的测量信息,实现对扭转振动的监测。
1 横向振动信号中扭振信号的提取
转子横向振动信号监测如图1 所示。一对相互垂直的电涡流传感器探测到的振动信号可表示为

图1 转子横向振动信号监测示意图Fig.1 Sketch of lateral vibration monitoring
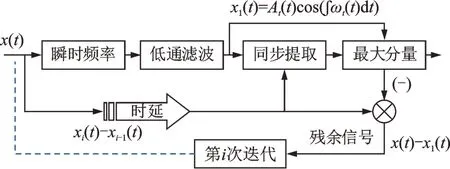
图2 Hilbert 分解流程图Fig.2 Block diagram of Hilbert decompose
其中:Ax(t),Ay(t)为瞬时幅值;ϕ(t)为瞬时相位。
对于实际转子系统,由于驱动力矩波动、扭转振动、装配误差、系统故障及弯扭耦合等因素的存在,会引起围绕平均转速的周期或准周期性的转速波动,转子的转速往往不能够保持恒定[15]。假定转子的平均角速度ω0=2πf0t,转速波动完全由扭振所引起,以x方向振动信号为例,有
其中:fτi,φi分别为各阶扭振频率及其初相角;下标i=1, 2, …,n;θ(t)为扭转变形角。
由式(2)可知,横向振动信号的相位会受到扭振的调制作用,即扭振频率将会被调制在相位中。横向振动信号还可以表示为
其中:H [·]表示Hilbert 变换;ϕ(t)为信号相位。
通过Hilbert 变换可以提取振动信号的瞬时相位,再对瞬时相位进行Hilbert 分解或频率检测,即可获取扭振的幅值和频率。
测量得到的振动信号中含有噪声、分频和倍频成分,使用带通滤波器提取一阶转频附近成分,经Hilbert 变换即可提取瞬时相位ϕ(t)
定义瞬时角频率为
由于一阶频率成分占据主导地位,这里仅考虑低阶扭振对相位的调制作用,且假定θ̇(t)=0,则根据上式可得瞬时角频率为
由式(6)可知,在频谱图上可以观察到基频两侧存在由扭振所导致的边频成分。可以通过Hilbert分解相位信号得到一阶扭振频率fτ1,进而求得扭振幅值a1。
在旋转机械中,往往存在非平稳、准谐波信号叠加的复合信号,如
其中:Al(t),ωl(t)分别为l阶分量下的瞬时幅值和频率。
对于此类非平稳信号,不便直接进行处理,通常会使用Hilbert 分解方法将其分成若干个成分单一的信号分量[16]。
Hilbert 分解流程如2 所示,具体的理论推导见文献[16]。横向振动信号中提取扭振信号的流程如图3 所示。

图3 横向振动信号中提取扭振信号的流程图Fig.3 Flowchart of extracting torsional vibration signal from lateral vibration signal
2 数值仿真验证
假定经过扭振频率调制后的横向振动信号为
其中:si(t)为各阶振动信号,下标i=1, 2, 3;n(t)为白噪声。
其中:α(t)为扭振相位角变化的缓变量(最大峰值为2°),用于模拟相位角随时间的波动。
以s1(t)为例,表示转速为2 400 r/min (40 Hz),扭振瞬时幅值最大峰值为20°,扭振频率取5.40 Hz。图4 为仿真信号的时域波形图和频谱图,仿真信号的长度为10 s。
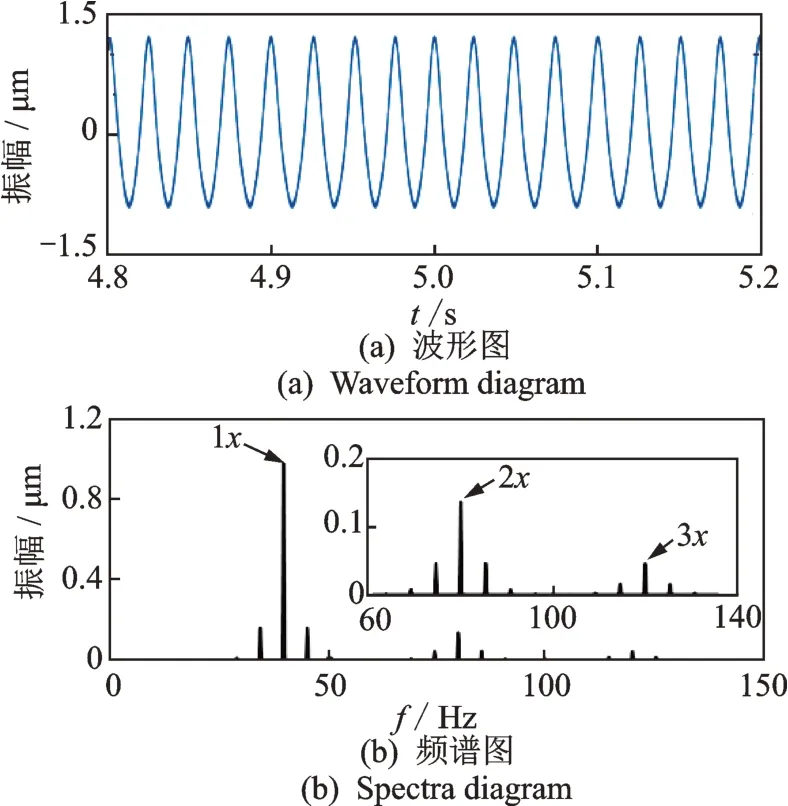
图4 仿真信号的时域波形图和频谱图Fig.4 Waveform and spectrum of simulated vibration signal
按照图3 所述的处理方法,提取得到的转频附近信号的时域波形图和频谱图见图5,并通过Hilbert 分解得到了扭振角的瞬时幅值和瞬时频率,如图6 所示。为尽可能消除边界效应对计算结果的影响,在扭振角的计算结果中截去了前后各0.5 s 的数据。从计算结果来看,得到的扭振频率的均值为5.41 Hz,与理论值5.40 Hz 仅仅相差了0.19%,说明该方法具有较高的准确度。同时,Hilbert 瞬时频率分析在理论上拥有无穷小的分辨率,可以捕捉到微弱的扭振频率变化。

图5 提取得到的转频附近信号的时域波形图和频谱图Fig.5 Waveform and spectrum of detected signal around 1x
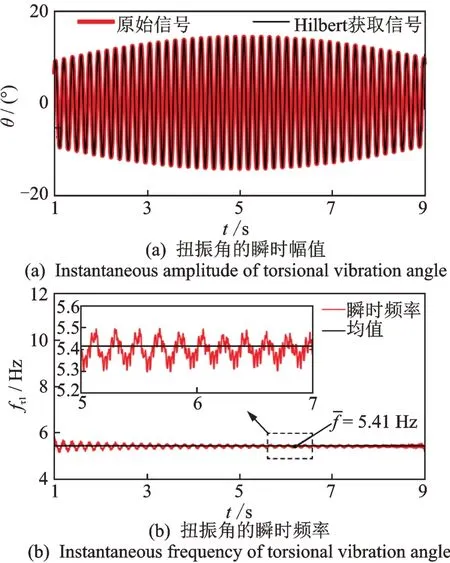
图6 扭振角的瞬时幅值和瞬时频率Fig.6 Instantaneous amplitude and frequency of torsional vibration angle
3 试验对比验证
3.1 试验过程
为验证所提方法的有效性,使用了如图7 所示的转子试验台。试验台由交流伺服电机驱动,非驱动端安装有编码器测量扭振,在盘2 的位置安装有电涡流传感器测量横向振动,并通过齿盘处的光电传感器测量转速。

图7 转子试验台Fig.7 Test rig of rotor
在5 000 r/min 转速下,同步采集了横向振动响应和编码器的扭振角信号,采样频率为10 kHz,时长为5 s。通过对比计算得到的扭振信息和编码器所测量的扭振信息,检验了所提方法的有效性。
3.2 试验数据分析
x和y方向的振动响应及其对数谱见图8。可以看到,在转频(83.3 Hz)两侧分别对应ω-fτ(54 Hz)和ω+fτ(112.6 Hz)的频率处各有一个峰值,这说明了弯扭耦合的存在。通过频率差可以计算出扭振频率为29.3 Hz,在图8(b)中很容易找出该频率对应的峰值,而在图8(d)中因为有其他频率成分的存在而不能很好地辨别出扭振频率。通过使用Hilbert 方法,计算得到的扭振频率如图9 所示,能够较为准确地计算出扭振频率。

图8 x 和y 方向的振动响应及其对数谱Fig.8 Vibration response and its logarithmic spectrum in x and y directions
图10,11 分别为通过编码器测量得到的扭振信号和其剔除转频及其倍频成分后的频谱图。测量得到的扭振信号与使用Hilbert 方法计算出的扭振信号如图12 所示。分析试验结果可以看出,使用Hilbert 方法计算出的扭振信息与测量值基本一致,频率相对误差仅为0.38%;受到边界效应的影响,前1 s 计算得到的瞬时幅值与真实值有较大偏差,但随着边界效应影响的减弱,二者能够较好地吻合。由于未能完全消除噪声和谐波成分的影响,测量扭振信号与计算所得结果存在一定的相位差,导致二者的时域波形不能完全对应。因此,对其有效值进行比较以评估幅值精度。经计算,使用本研究方法所提取的扭振信号有效值与测量信号有效值的绝对误差为0.025°,相对误差为25.38 %。由于扭振角本身较小,即使是很小的偏差也可能会导致较大的相对误差值,但总体而言,本研究所提方法是可行且有效的。

图11 滤波处理后的扭振信号频谱图Fig.11 Spectrum of filtered torsional vibration signal

图12 测量扭振信号与计算扭振信号Fig.12 Measured torsional vibration signal vs calculated torsional vibration signal
4 工程验证
使用如图13 所示的工业级透平压缩机试验台进行相关验证,该试验台由变频器控制的三相异步电机进行驱动,经齿轮箱增速进行工作,齿轮箱速比为1∶5。

图13 离心压缩机试验台Fig.13 Centrifugal compressor experimental platform
在2 个轴承座上分别安装一对位移传感器以采集横向振动信号。记录试验台在工作转速为2 100 r/min 时的振动信号,时间长度为30 s,采样频率为3 kHz,x方向振动响应及其频谱如图14 所示。
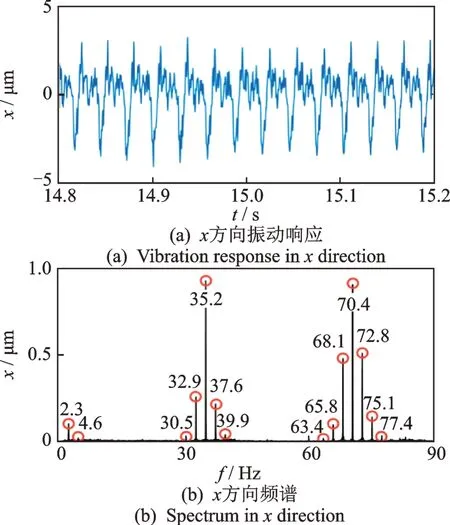
图14 x 方向振动响应及其频谱Fig.14 Vibration response and its logarithmic spectrum in x direction
由图14(a)可以看出,横向振动的波形受扭振的影响很大,调制作用十分明显。由图14(b)中的低频段可以明显观察到扭振频率及其2 倍频的存在,在转频和2 倍转频附近的边频带则是由中心频率与扭振频率的和差频率形成的。这说明在实际提取扭振频率时,不仅可以从1 倍频入手,2 倍频及更高的倍频成分也可以用于提取扭振信息。由频谱分析可知,扭振对于倍频的影响更为明显,通过分析倍频成分来提取扭振信息可能会有更好的效果。
使用本研究所提方法计算得到的扭振频率见图15,可知扭振频率为2.3 Hz,验证了文献[17]的研究结果,也进一步验证了本方法的可行性与准确性,能够为工程中的扭振测量提供新的测试途径。

图15 计算得到的扭振频率Fig.15 Calculated frequency of torsional vibration
5 结 论
1) 通过Hilbert 振动分解可以将调制在横向振动中的扭振信息进行分解,逆变为原始的扭转振动信号,进而获得扭转振动的幅值和频率。
2) 由扭转振动引起的转速波动反应在转速频率上十分微小,使用传统的离散傅里叶频谱分析方法对横向振动进行分析难以捕捉到微小的转频变化。笔者提出的信号分析方法可以精确获得扭振的信号特征,且Hilbert 瞬时频率分析方法在理论上的分辨率可达无穷小,适用于探测微弱的扭振波动频率。
3) 解析信号的模拟仿真和试验测试结果均表明,所提出的扭振信号提取方法具有较高的频率测试精度,仿真和试验结果的最大误差率分别为0.19%和0.38%,为扭转振动的工程测试提供了一种便捷途径。
4) 现有方法中,扭振幅值受边界效应及信号噪声的影响,仍存在较大的误差 。

