关于麦克劳林公式中余项的注记

章江华, 王成伟

(北京服装学院 文理学院,北京 100029)

0 引 言

在某点处高阶可导的函数可以表示为泰勒多项式及其余项的和.该泰勒多项式可用于近似计算,其相应的拉格朗日型余项可用于该近似的误差分析.利用符号计算工具包容易求得一个函数的泰勒多项式,但当作误差分析时,往往需要手工推导泰勒公式中的余项.值得注意的是拉格朗日型余项形式有时不是唯一的,比如文献[1-2]给就出了“拉格朗日型余项Rn(x)用函数的(n+1)阶导数、(n+2)阶导数表示均可”的结论.本文将注解由该“不唯一”造成的应用拉格朗日型余项作误差分析时余项形式选择问题,让泰勒公式及其余项形式的理解更细致.

为简单且不失一般性,下面仅涉及函数在x0=0处的泰勒公式,即麦克劳林公式.

设函数f(x)在含原点的某个开区间(a,b)内具有直到n+1阶导数,那么对于(a,b)内任一非零的x,有

f(x)=pn(x)+Rn(x),

(1)

其中

(2)

(3)

称(1)式为函数f(x)的带有拉格朗日余项的n阶麦克劳林公式;称(2)式为函数f(x)的n阶麦克劳林多项式,若f(n)(0)≠0,称(2)式为函数f(x)的n次麦克劳林多项式;称(3)式为函数f(x)的n阶拉格朗日型余项.

通过求函数f(x)的n+1阶导数再代入(1)(2)(3)式而获得麦克劳林公式的方法称为直接法. 通过基本初等函数的麦克劳林公式运算求得麦克劳林公式的方法称为间接法.文献[3]中注明直接法或间接法求得的同次麦克劳林多项式pn(x)是相同的,没有给出相应的拉格朗日型余项形式的论述.文献[4]中论证了pn(x)是近似f(x)精度最高的多项式.下面将从两个方面对麦克劳林公式中的余项形式展开讨论,指出直接法或间接法求得的同次麦克劳林多项式pn(x)所对应的余项形式不一定相同.从泰勒公式解决问题本意看,间接法得到的余项也有价值,用于误差分析有时效果更好.

1 麦克劳林公式阶数及其余项形式的选择

利用麦克劳林公式求给定次数的麦克劳林多项式时,麦克劳林公式的阶数可能不同,相应的余项形式也会不同.一般地,选取阶数高的余项形式作误差分析精度更好.

例1求sinx的带有拉格朗日型余项的n阶麦克劳林公式.

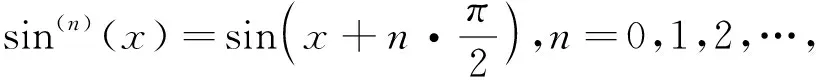
故带有拉格朗日型余项的n阶麦克劳林公式为

(4)

简化

于是

当n=2m时,(4)式为

(5)

当n=2m+1时,(4)式为

(6)

注1 (5)式中有“0·x2m”项,说明sinx的2m(偶数)阶麦克劳林多项式是2m-1(奇数)次多项式.当n=2m+2时,(4)式为

观察(6)与(7)式可以发现,麦克劳林多项式是相同的,余项形式不同,麦克劳林公式的阶数不同.

从应用的角度看,用于近似计算sinx的2m+1次多项式可由2m+1阶麦克劳林公式(6)式获得,也可由2m+2阶麦克劳林公式(7)式获得,但相应的余项形式不同.显然,用阶数高的余项形式作误差分析精度更好.

同理,cosx的带有拉格朗日型余项的n阶麦克劳林公式也可作类似的讨论.即cosx的带有拉格朗日型余项的2m阶麦克劳林公式为

(8)

cosx的带有拉格朗日余项的2m+1阶麦克劳林公式为

当近似计算cosx所采用的多项式次数给定时,利用(9)式中的余项作误差分析精度比用(8)式好. 因此,在教材[3-7]中只给出(9)式型公式.

需要注意的是教材[3-7]配置的习题有“写出函数的麦克劳林公式”,成了没有考虑到上述细节的读者的难点.为保持认知一致性,建议从近似计算的角度来配置习题,或在教材中写入上述细节,让表述更清晰.

一般地,当f(n)(0)=0时,函数f(x)的带有拉格朗日型余项的n阶麦克劳林公式中的pn(x)是低于n次的多项式.故从近似计算角度看,当选取一定次数的麦克劳林多项式后,作误差分析时,选取麦克劳林公式的阶数高的余项形式,精度更高.

结论1若函数f(x)在含原点的某个开区间(a,b)内具有直到n+1阶导数,且函数f(x)在x0=0的某阶(比如f(i)(0)=0)导数为零,则用于近似计算f(x)的某次(比如i-1次)麦克劳林多项式对应的余项有不同的形式,阶数高的余项形式精度高.

2 间接法获得的余项与直接法获得的余项的比较

例2求函数f(x)=sin2x的带有拉格朗日型余项的n阶麦克劳林公式.

故带有拉格朗日型余项的n阶麦克劳林公式为

(10)

简化

于是

当n=2m+1时,(10)式为

(11)

当n=2m时,(11)式可表达为

(12)

所以sin2x的带有拉格朗日型余项的2m+1阶麦克劳林公式为

(13)

若利用cosx的带有拉格朗日型余项的2m阶麦克劳林公式(8)得

所以sin2x的带有拉格朗日型余项的2m阶麦克劳林公式为

(14)

注2 比较(11)与(13)式或(12)与(14)式可发现直接法与间接法所得余项形式上是一样的.

例3求f(x)=xex的带有拉格朗日型余项的n阶麦克劳林公式.

解 直接法因为f(n)(x)=(n+x)ex,n=0,1,2,…,所以

f(n)(0)=n,f(n+1)(θ13x)=(n+1+θ13x)eθ13x, 0<θ13<1.

故带有拉格朗日型余项的n阶麦克劳林公式为

(15)

间接法利用ex的带有拉格朗日型余项的n阶麦克劳林公式,得

(16)

注3 由定义可判断(16)式不是xex带有拉格朗日型余项的n阶麦克劳林公式.为比较(16)与(15)式中的余项,将用于近似计算xex的多项式取为同次.由(15)式得xex带有拉格朗日型余项的n+1阶麦克劳林公式

(17)

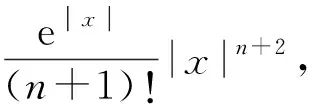
结论2间接法获得的麦克劳林多项式及其余项的和不一定是麦克劳林公式,但其误差分析的价值优于直接法获得的麦克劳林公式.

3 结 论

泰勒公式中的余项是近似计算中误差分析的基础,加深其认识具有重要的意义.通过3个例子的麦克劳林公式的求解结果说明用于近似计算的多项式给定次数后,余项可能有多种表达形式,高阶的精度更高.间接法获得的余项虽然不一定满足拉格朗日型余项标准形式,但是也具有误差分析的价值.建议在教材中补充余项讨论的细节,引入“n阶麦克劳林多项式”的称谓,使思维更清晰,降低难度.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.