以单元整体教学培养学生高通路迁移能力

赵桂枝

［摘要］ 数学知识之间存在着复杂的关联性，依据不同的知识主线可以构建出不同主题的单元整体，从单元整体出发进行教学设计，可促进学生理解知识的内在联系，培养高通路迁移能力。以人教版初中数学“圆内接四边形的定义及性质”为例，对比以课时为单位的教学设计和从单元整体出发的教学设计，探讨单元整体教学培养学生高通路迁移能力的策略。

［关键词］ 单元整体教学；高通路迁移；核心素养；圆内接四边形

迁移是指把一个情境中学到的知识迁移到新情境中的能力。当新任务与原任务相似时，称为“低通路迁移”；当新任务与原任务不相似时，称为“高通路迁移”。以人教版“圆内接四边形的定义及性質”为例，《义务教育数学课程标准（2022年版）》（以下简称《课标》）在第四学段关于圆的内容要求中指出：了解并证明圆内接四边形的对角互补。圆内接四边形是与圆有关的特殊的四边形，特殊在四边形的四个顶点在同一个圆上，这一特殊的位置关系决定了圆内接四边形的对角之间具有特殊的数量关系。初中阶段，学生在学习平行四边形和特殊的平行四边形时，已经积累了一定的研究特殊四边形的方法，能否自觉地将研究平行四边形的方法迁移至圆内接四边形的研究，进而迁移至一般图形的研究，是对学生高通路迁移能力的检验。因此，通过对比以课时为单位的教学设计和从单元整体出发的教学设计，尝试研究如何通过单元整体视角的教学设计，来培养学生的高通路迁移能力。

一、重构认知体系为高通路迁移打通知识脉络

建构贯通的认知结构是高通路迁移的重要前提。以课时为单位的教学设计，知识结构具有紧密性和线性关联的特点。学生的短时记忆可以弥补理解力和迁移能力的不足，从而形成“教学顺畅”的课堂表象。但学生往往对所学知识内容之间的关联理解不深，久而久之就会陷入“一学就会、一做就错”的困境。单元整体视角的教学设计，是在知识体系中设计教学，知识结构具有松而不散、立体关联的特点，同时将新知识纳入学生原有的知识体系，其重新建构的过程即高通路迁移能力形成与发展的过程。

作为圆周角定理的推论，人教版初中数学教材将关于“圆内接四边形的对角互补”的教学内容设置在第24章第1节第4课时“圆周角”的位置。首先，给出圆内接多边形和多边形的外接圆的定义，然后再以举例的方式给出圆的内接四边形和四边形的外接圆，并提出问题：圆内接四边形的4个角之间有什么关系？通过证明，最后得出结论。

对于以课时为单位的教学设计，重点是圆内接四边形的性质，难点是构造圆心角。为了突出重点、突破难点，教师往往更加关注与圆周角和圆心角有关的知识（圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半）复习，通过唤起记忆的方式引导学生“发现”添加辅助线的方法。而圆内接四边形本质上属于特殊的四边形，其研究方法与在第18章研究平行四边形和特殊的平行四边形类似。

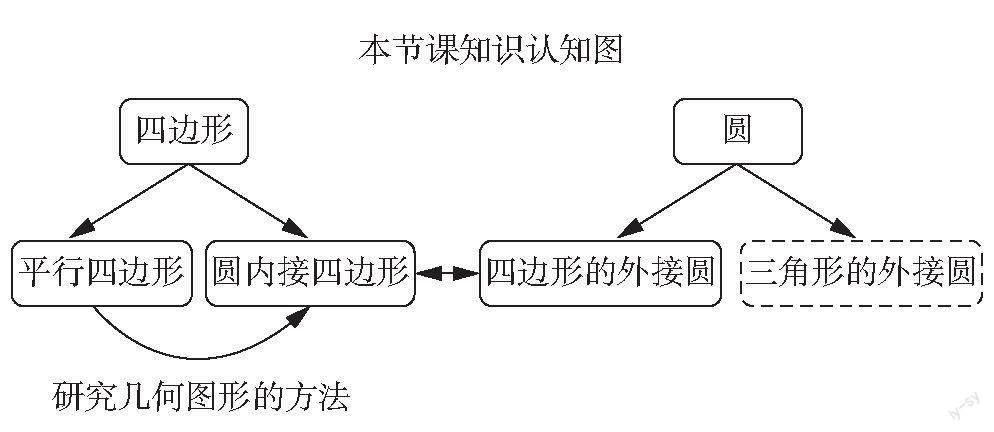
与其相关的知识还有圆内接三角形，在本章第2节第1课时点和圆的位置关系中给出：不在同一条直线上的三个点确定一个圆。要将与圆内接四边形有关的知识整合在一起，形成一个“单元整体”，从而在这个单元整体下进行教学设计，重点是掌握研究特殊图形的方法，难点是发现圆内接四边形是一种特殊的四边形。这就需要引导学生在圆和四边形这两块知识之间建立联系。为此，教师设计了如下图的知识联结式引入：

那么，圆和四边形相遇，会不会产生一种新的特殊的四边形呢？可让学生作图来验证。

学生的作图顺序有两种。一种是先画圆，再画四边形。这种做法，学生会关注到四边形的顶点、边和角与圆的位置关系。另一种作图顺序是先画四边形，再画圆。这种做法学生会关注圆心与四边形的边的位置，圆半径的选取对图形的影响。学生未必能够画出“圆内接四边形”，但作图的过程即学生将圆的组成要素（圆心、半径）和四边形的组成要素（顶点、边、角）建立关联的过程。这样，学生知识体系中的圆和四边形在作图中形成联结，进而在潜移默化中形成知识体系的重构，为研究方法的迁移搭建起贯通式的知识架构。

二、开放思维空间为高通路迁移延展理解边界

理解研究对象的本质属性是高通路迁移的必备能力。以课时为单位的教学设计，学生的课堂学习比较聚焦，但同时也限制了思维的延展。基于单元整体进行教学设计，因其知识跨度比较大，教师则要给学生提供开放的思维空间，推动学生突破思维边界的限制。

以课时为单位，研究圆内接四边形的教学关注“运用圆周角定理证明圆内接四边形的对角互补”，学生沿着圆周角的方向思考即可。而在单元整体中，这节课的教学更关注“如何将研究平行四边形的方法迁移至研究圆内接四边形”。虽然这一方法在研究平行四边形的时候已经多次使用，但从学习平行四边形到学习圆内接四边形，时间间隔比较长，学生的短时记忆作用已经不明显。此时，学生需要认识到圆内接四边形和平行四边形之间的本质关联，才能够想到研究方法的迁移。这就要求教师在课堂教学中给学生提供开放的思维空间，引导学生发现特殊四边形的共性，通过将研究特殊平行四边形的方法迁移至对圆内接四边形的研究，进而迁移至一般图形的研究，即应用“观察、测量、猜想、证明”的方法研究几何图形。

具体教学过程中，教师设计开放性问题：如何研究圆内接四边形的性质呢？主要的步骤：（1）分组探究。每组4-6人，分别对圆内接四边形的边、角、对角线通过观察、测量、猜想、证明的方法进行研究。（2）分

享交流。通过作图、观察和测量学生能够发现圆内接四边形的边和对角线没有特殊的数量关系和位置关系。圆内接四边形的对角有特殊的数量关系即相加等于180°。（3）推理求证。学生板书证明过程，得出结论：圆的内接四边形的对角互补。（4）归纳提炼。教师揭示探究过程中体现的高通路迁移能力：圆内接四边形是一种特殊的四边形。它的特殊性表现在位置上是四个顶点在同一个圆上，表现在数量上是对角互补。研究圆内接四边形的方法与研究平行四边形、矩形、菱形的方法相似，即从边、角、对角线三个维度，通过观察、测量、猜想和证明得出结论。这一研究过程应用了分类和转化的思想，这种方法不限于研究四边形，对其他几何图形，也可以根据图形的关键元素分类，通过观察、测量、猜想和证明来进行研究。

三、培养核心素养为高通路迁移提供生长动能

数学核心素养是高通路迁移能力持续发展的原动力。初中阶段，数学学科核心素养的内涵可分为三个层面：会用数学的眼光观察现实世界、会用数学的思维思考现实世界、会用数学的语言表达现实世界。核心素养是在数学学习过程中逐渐形成和发展的。单元整体视角的教学设计对核心素养的培养，具有前后呼应、循序渐进的特点。

本节课以单元整体设计的教学，将圆内接四边形作为知识主线，单元内各部分的任务及相关核心素养内涵，具体如下表所示。其中，贯穿单元始终的核心素养主要表现在几何直观和推理能力这两个方面。

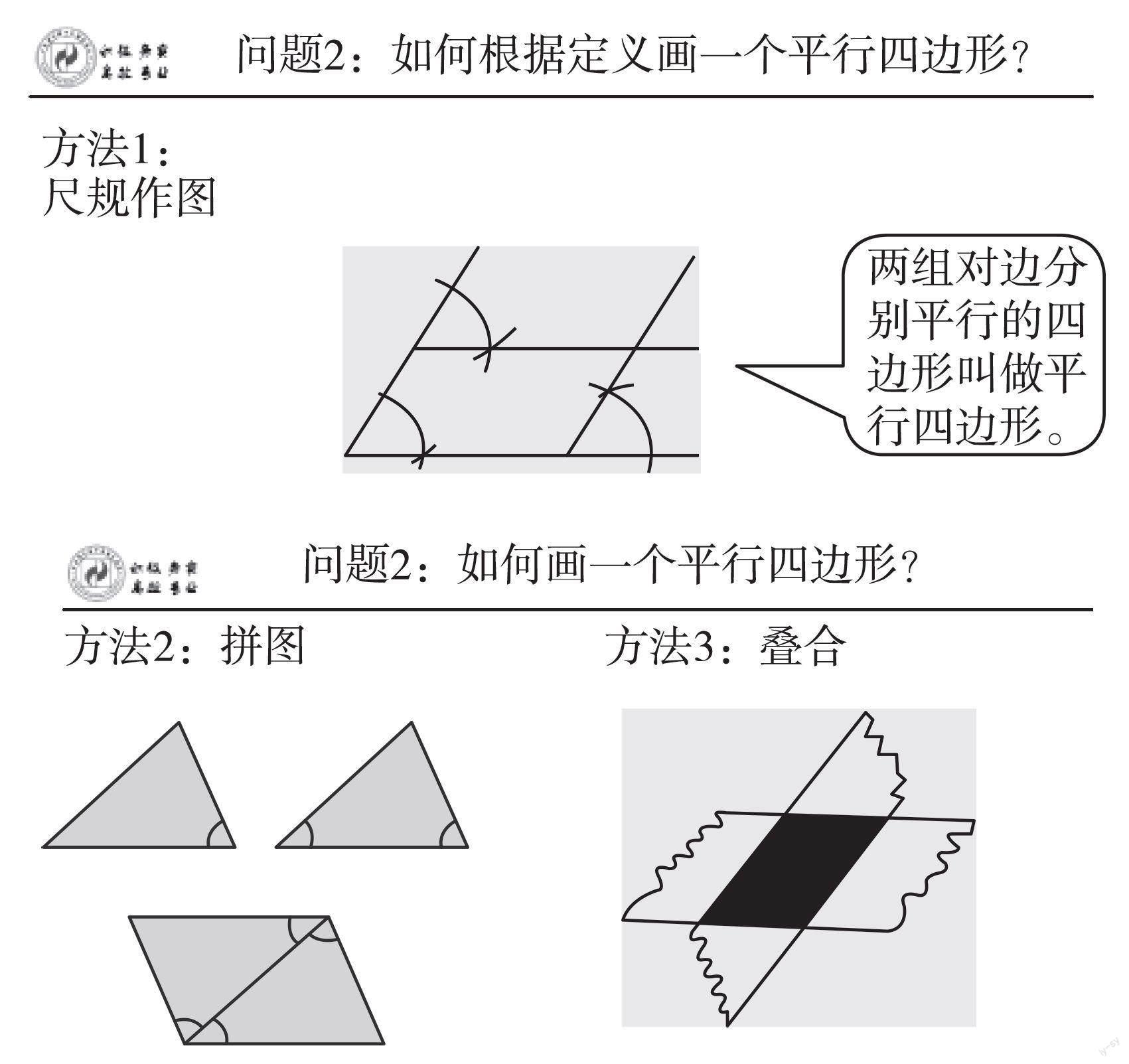
以几何直观的培养为例，基于单元整体的教学设计，更注重通过作图来培养学生的几何直观，即“根据语言描述画出相应的图形”。为此，在单元起始部分的“平行四边形”教学中，教师一开始就为圆内接四边形的作图做准备，如在介绍了平行四边形的定义（两组对边分别平行的四边形叫做平行四边形）之后，适时引导学生画若干个不同的平行四边形，并根据学生的作图总结出如下方法：

方法一：利用尺规作图画平行四边形。

方法二：利用两张全等的三角形纸片拼出平行四边形，再沿边把它画出来。

方法三：将两张对边平行的纸条交叉叠放，沿重合部分的边可画出一个平行四边形。

《课标》在课程实施部分中指出，要改变过于注重以课时为单位的教学设计，推进单元整体教学设计，体现数学知识之间的内在逻辑关系，以及学习内容与核心素养表现的关联。实际上，这里的单元可以是教材中自成一体的单元，如一次函数；也可以是多章组合的单元，如将一次函数、二次函数、反比例函数合而为一构成初中函数单元；还可以是以某个知识为主题、由与其具有核心素养强关联的知识组成的单元，如本文的案例“圆内接四边形”，以“直角三角形”为主题的单元整体可由以下内容组成：余角和补角、等邊三角形、勾股定理、勾股定理的逆定理、矩形、锐角三角函数等。

总之，从单元整体出发设计数学教学，有助于学生突破思维的边界，促使学生把握不同事物之间的本质关联，明晰思维的路径，实现在不相似的任务中完成迁移，从而更有效地培养解决问题的能力。

［参考文献］

［1］刘徽.大概念教学：素养导向的单元整体设计[M].北京：教育科学出版社，2022.

［2］中华人民共和国教育部.义务教育数学课程标准（2022年版）[S]北京：北京师范大学出版社，2022.