探寻本源 “点”到为止
——例谈基于点坐标运算的解析几何复习策略
苏卫军
(义乌中学,浙江 义乌 322000)
1 问题提出
解析几何的本质是通过建立坐标系并利用代数运算的方法来研究圆锥曲线的几何要素与几何性质等,即通过建系、设点、列式、运算等步骤和方法来研究直线和圆锥曲线(包括圆、椭圆、双曲线、抛物线等)的相关性质,简而言之就是几何(图形)问题坐标化.解析几何的题型千变万化,但万变不离其宗.高三阶段对于解析几何内容的复习仍然要着力培养并强化学生回归本质与探寻本源的意识,培养学生善于抓住圆锥曲线上的动点及其坐标来分析问题的意识,培养学生灵活地利用动点坐标的多种表达形式去解决相关问题的能力.学生能熟练地掌握圆锥曲线上点坐标的多种表达形式,同时善于代入问题情境进行灵活的代数运算,并最终顺利地解决相关问题,这是在高三解析几何复习中需要追求和达成的目标.
在解析几何的复习课教学中,仍然要着眼于发展和提升学生的数学运算和数学抽象两大核心素养.一方面,要夯实学生数学运算的基本功,通过必要且必需的运算使学生数学运算的核心素养得以发展;另一方面,也要引导学生从纷繁复杂的代数运算中找到化繁为简的路径,并充分利用等价转化、整体代换等思想和方法,使数学抽象的核心素养得以夯实与提升.
2 真题分析

1)求W的方程;

(2023年全国数学新高考Ⅰ卷第22题)
分析学生在考场上面对此题,最大的困惑与障碍在于题目中涉及的动点个数太多(有4个动点)以及动点坐标的不确定性,以至于分析问题缺乏头绪并最终导致思维受阻.对于此题的分析,应透过现象看清本质,即首先要注意到矩形(4个顶点)其实是表象,三角形(3个顶点)才是本质,因为矩形周长可以转化为两个全等直角三角形直角边之和.在此基础上,再大胆地进行设点求解(抛物线上的点坐标是可以直接根据抛物线方程来表示和代换的),通过坐标代换又能很快地得出相应直线的斜率与点坐标的关系,最后通过代数运算即可求解.

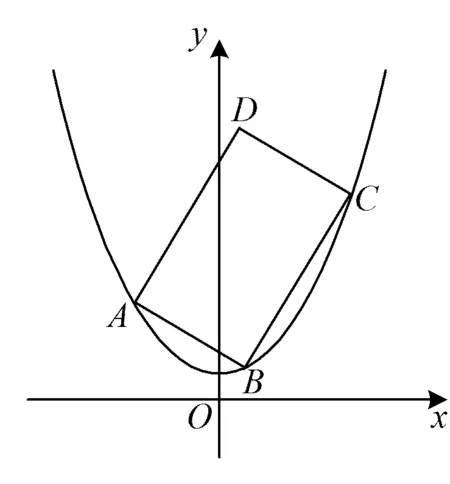
图1
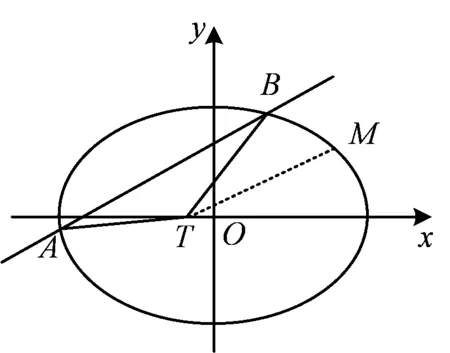
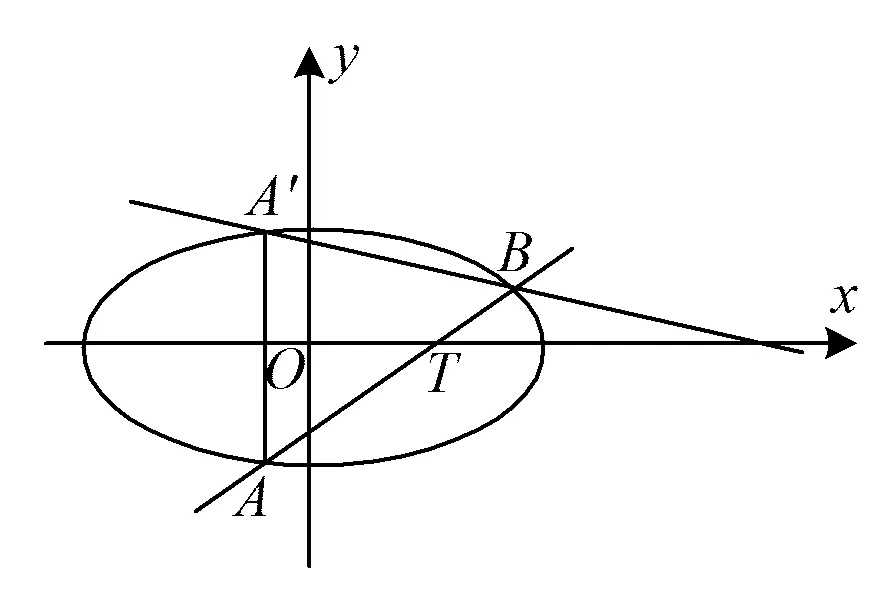
kABkBC=-1,a+b kBC=b+c. 令kAB=m<0,kBC=n>0,则 mn=-1, 即 设矩形周长为L,由对称性不妨设|m|≥|n|,则 从而L=2(|AB|+|BC|) 即 即 m2=n2, 评注对于抛物线上多个点坐标表示的代数式,往往需要先进行整体代换(换元),然后再进行必要的讨论和运算,这是解决与抛物线有关问题的常见策略,也是学生需要具备的基本功.在高三复习的过程中,教师要重视培养学生在这些方面的能力和基本功.事实上,对含根号的式子进行换元的方法有很多种,教师要善于培养学生的发散性思维,结合多元视角,寻求多种方法解决相关问题. 同理可得 kBC=b+c, 又 (a+b)(b+c)=-1, 则 |AB|+|BC| a=-cotθ-b,c=tanθ-b, 从而 |AB|+|BC| 又b≥0,故 于是 |AB|+|BC| 故 评注对于抛物线上的点A,B,C,我们还可以把它们看成在相应的直线上,再引入直线的参数方程来求解相应问题. (a+b)(b+c)=-1. 由对称性不妨设a<0≤b 又点C在W上,则 即 同理可得 又因为 t1>0, 所以 0≤2b 从而 评注从以上问题的分析和求解过程可以看出:对于解析几何中与圆锥曲线的内接三角形(四边形)的周长和面积等有关的问题,在解题和教学中要善于探寻本源、抓住本质,紧紧围绕曲线上点坐标的不同表达形式,采用合理、有效的方式进行设点.圆锥曲线上点坐标的表达方式是丰富多彩的,可以利用圆锥曲线的标准方程来表示,还可以利用直线的参数方程来表示.在实际的问题情境中,往往需要具体问题具体分析,选择合适的表达方式进行求解.此外,对于圆锥曲线上的点,还有一种非常重要的坐标表示方法,即利用圆锥曲线的参数方程进行代换. 分析此题若采用设直线方程(即设直线l的方程为y=kx+m)的形式,并结合根与系数的关系来求解问题,则相应表达式会比较复杂并且运算量较大.通过分析比较,采用椭圆的参数方程来设点求解,运算量会大大简化. 解设A(acosα,bsinα),B(acosβ,bsinβ),则 P(a(cosα+cosβ),b(sinα+sinβ)). 由于点P也在椭圆上,故把点P坐标代入椭圆方程并化简可得 从而S=2S△OAB=ab|sinβcosα-cosβsinα| 解设A(acosα,bsinα),B(acosβ,bsinβ),则 (等号成立条件略). 事实上,圆锥曲线上的点坐标不仅可以用圆锥曲线的标准方程、参数方程以及直线的参数方程等来表示,还可以利用向量的坐标(有时也会采用复数的坐标)来表示点的坐标,以此达到化多为少、化繁为简的目的,这在竞赛、强基和三位一体等测试中会经常用到. 例3在平面直角坐标系中,点A,B,C在双曲线xy=1上,满足△ABC为等腰直角三角形,求△ABC面积的最小值. (2020年全国高中数学联赛试题第11题) 分析对于双曲线上的动点,如果用3个坐标表达已知条件,代数式的整体变形(换元)会比较困难.为此,寻求用向量坐标来表达点坐标的形式,使条件的转化更加直接,运算更加流畅. 由点B,C在双曲线xy=1上,可知 等价于 (1) (2) 式(1)+式(2),得 式(1)×式(2),得 由基本不等式可得 (s2+t2)4=[-s2t2(s2-t2)]2 在高三解析几何复习中,要充分关注涉及两点连线的距离和斜率问题,比如探究等腰三角形是否存在、椭圆与圆的公共点个数等,以及圆锥曲线的割线和切线等问题,这些问题的求解往往需要回归本源,牢牢抓住圆锥曲线上点坐标的整体表示来解决问题. 案例1椭圆中动点与定点连线的距离和斜率等问题. 即 证明过程略. 图2 (1992年全国数学高考理科试题第28题) 分析此题是一道非常经典的好题,证明方法很多,但最能回归本源、体现问题本质的方法是利用距离公式化为二次函数来求解. 解(等价转化)设M(x,y)为椭圆上的动点,联结MT,则 由题意知在|MT|的所有可能取值中必有两个点A,B满足|AT|=|BT|,又由于直线AB与x轴不垂直,故函数 图3 (2016年浙江省数学高考理科试题第19题) 解设P(x,y)为椭圆上的动点,则 考虑函数z=(1-a2)y2-2y+a2+1(其中-1≤y≤1)的图象与直线z=r2的公共点,其中a>1,r为圆的半径.当公共点对应的y=-1时,1个公共点对应圆与椭圆的1个公共点;当公共点对应的y∈(-1,1)时,1个公共点对应圆与椭圆的2个公共点.根据题意知,函数z=(1-a2)y2-2y+a2+1(其中-1≤y<1)为单调函数.因为函数的对称轴为 所以 评注椭圆上点坐标的平方代换,能实现化双变量函数为单变量二次函数的目的.对学生而言,当把问题的本质化为二次函数的时候,所有问题的求解都将变得轻车熟路了.在平时的复习中也要关注到,椭圆上点坐标的平方代换,还能将斜率的非对称结构化为对称结构. 图4 且 y1=kx1+m,y2=kx2+m, 得 从而 此式即为对称结构,往后过程略. 案例2圆锥曲线中的割线与切线方程问题. 切线问题是解析几何中一类非常经典的问题,求解策略很多,比如方程组联立判别式为0,先化为函数再求导得斜率等.但在高三复习课教学中,教师可以站得更高一些、看得更透一些,不妨回归本源,将问题的本质归结到从圆锥曲线的割线过渡到切线的过程,并进一步回归到利用圆锥曲线上点坐标的整体表示以及相应代数运算上来. 结论3过抛物线y2=2px上两点A(x1,y2),B(x2,y2)的直线方程的对称式结构为 2px-(y1+y2)y+y1y2=0. 去分母并移项,整理得 2px-(y1+y2)y+y1y2=0. 特别地,当点A,B与抛物线上的点P(x0,y0)均重合时,割线AB变为过点P(x0,y0)的切线l.此时 x1=x2=x0,y1=y2=y0. 从而切线l的方程为 即 a2(y1+y2)y+b2(x1+x2)x-(a2y1y2+b2x1x2+a2b2)=0. 证明由点差法可得 则直线AB的方程为 去分母并移项,整理得 a2(y1+y2)y+b2(x1+x2)x-(a2y1y2+b2x1x2+a2b2)=0. 特别地,当点A,B与椭圆上的点P(x0,y0)均重合时,割线AB变为过点P(x0,y0)的切线l.此时x1=x2=x0,y1=y2=y0,从而切线l的方程为 a2y0y+b2x0x-a2b2=0, 即 证明可用同构法,过程略. 评注以上结论的本质即为圆锥曲线中的极点和极线问题,是解析几何中非常经典的问题. 图5 解设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),可知抛物线上过点A,B的直线方程为 (y1+y2)y=x+y1y2. 将点Q(4,1)代入上式,得 (y1+y2)=4+y1y2, 即 (y1-1)(y2-1)=-3. 同理可得 lAC:(y1+y3)y=x+y1y3. 将N(2,1)代入上式,得 (y1+y3)×1=2+y1y3, 即 (y1-1)(y3-1)=-1. 同理可得 (y2-1)(y4-1)=-1, 从而 =[(y1-1)(y2-1)]2=9. 图6 同理可得,直线A′B的方程为 从而 于是 (3) 代入式(3),得 评注以上问题的本质即为圆锥曲线中的极点与极线问题. 在高三解析几何的复习过程中务必要讲求实效、讲究策略,要注重探寻本源、回归本质,在复习中要利用好大单元和大概念的理念来统领整章的知识和方法线索.同时,在课堂教学中要多给学生独立思考的时间,培养他们主动去发现问题、提出问题、分析问题和解决问题,还要关注学生学习和思维的全过程,着力提升学生的数学运算和数学抽象核心素养以及发散性思维等.高三的复习课教学尤其是解析几何这部分内容的复习课教学绝不能大搞题海战术,题海战术并不能从根本上提高学生的能力.高考试题灵活多变,教师在课堂教学中务必要在基本概念、基本思想和基本方法上下功夫,注重提高学生的数学素养和思维能力,只有这样,学生才能在最后的选拔中脱颖而出.


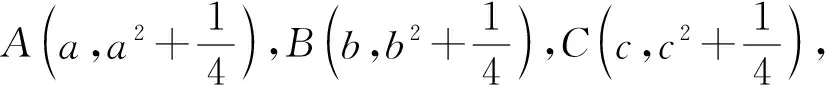
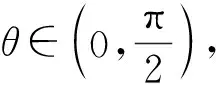

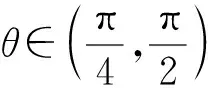
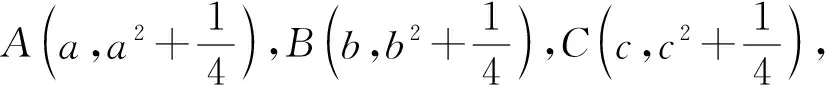



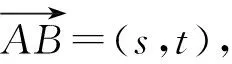
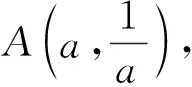
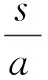


3 本源探寻——基于圆锥曲线标准方程的动点坐标代换问题


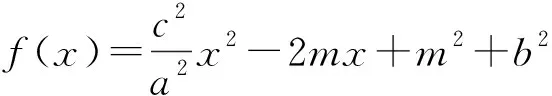








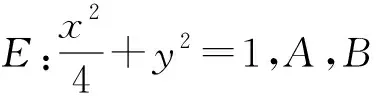

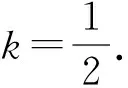
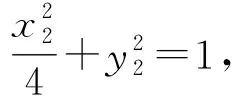




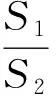
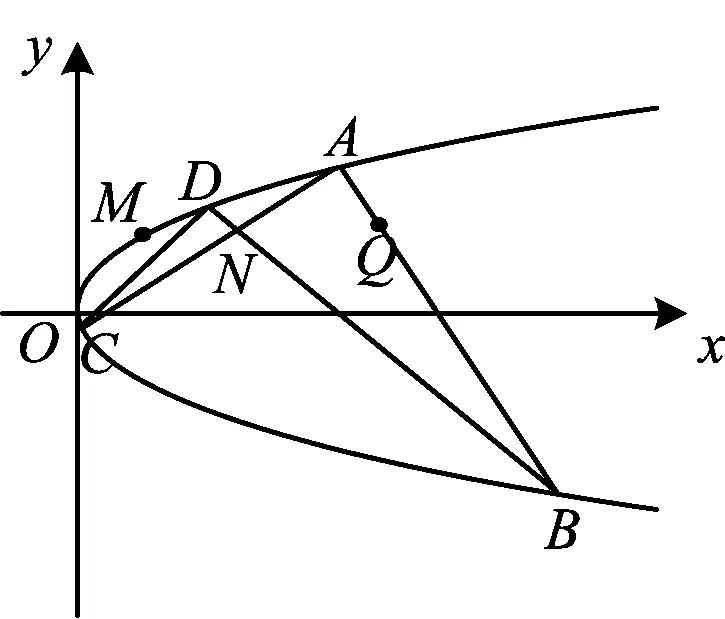
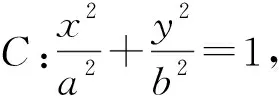
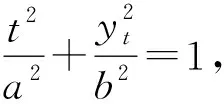
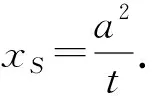
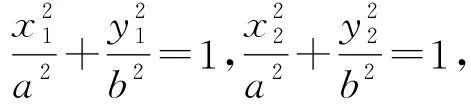


4 反思感悟

