基于智慧课堂下高三一轮复习课教学研究

【摘  要】  随着时代发展，科学技术对学校发展也起到了促进作用.而智慧课堂平台作为一种工具，弥补了传统教学的不足，也对传统教学作出了补充.其数据统计功能让老师更好地把握学情，设计教学内容，提升教学效率.文章以具体教学设计说明如何运用智慧课堂实施复习课的教学.

【关键词】  高三一轮复习；二项式定理；教学设计；智慧课堂

1  问题提出

《普通高中数学课程标准（2017年版）》指出，“注重信息技术与教学课程的深度融合，提高教学的时效性.”“鼓励学生运用信息技术学习、探索和解决问题.”“教师要适应时代的发展，按照课程标准的要求发挥信息技术的直观便捷、资源丰富的优势，帮助学生发展数学学科核心素养.”［1］但在智慧课堂环境下，如何实现教学决策数据化、评价反馈即时化、交流互动立体化、资源推送智能化，以及创设有利于协作交流和意义建构的学习环境，通过智慧的教与学，促进全体学生实现符合个性化成长规律的智慧发展，是我们一线老师重点思考的问题.在各类课型中，教师又该如何更好地利用智慧课堂平台设计科学的教学方案，提升教学效率呢？本文以二项式定理一轮复习教学设计为例，说明在智慧课堂环境下设计复习课型的教学具体思路.

2  智慧课堂教学流程

利用智慧课堂平台的强大数据统计功能，在课前设计好练习题并收集数据进行分析，以此确定学情，在课中可以统计学生解题情况.在课后，可以根据课前与课中的数据精准推送作业.一般流程如图1所示［2］.

3  基于智慧课堂环境下的教学设计

3.1  课前练习收集数据，确定教学重难点3.1.1  二项式的项数

（1）二项式（a+b）6的展开式共有（  ）项.

A.5    B.6    C.7    D.8

3.1.2  關于项的系数

（2）在x+2x3的展开式中，常数项为（  ）.

A.1    B.3    C.6  D.12

（3）二项式x6+1xx5的展开式中为常数项的是（  ）.

A.第3项   B.第4项   C.第5项   D.第6项

（4）在（x2+3x+2）5的展开式中x的系数是（  ）.

A.160    B.180    C.240    D.2103.1.3  赋值法求系数和

（5）已知（x－1）10=a0+a1x+a2x2+…+a10x10，则a0+a1+a2+…+a10=（  ）.A.210  B.0  C.1  D.-1

（6）设（2x－3）4=a0+a1x+a2x2+…+a4x4，则a0+a2+a4=（  ）.

A.311    B.312    C.313    D.315

3.1.4  二项式系数性质

（7）在x2－1xn的展开式中，只有第五项的二项式系数最大，则展开式中常数项是（  ）.

A.-7  B.7  C.－358  D.358

（8）在x－2xn的展开式中，第四项和第五项的二项式系数相等，则展开式的有理项的项数是（  ）.

A.5    B.4    C.3    D.2

设计意图  课前练习要根据模块知识内容精选典型的题目，选题的标准是能体现本内容的基础知识、相应的技能以及重要或常用的思想方法［3］.题目也不应过难，学生能在课前回顾课本知识内容即可解决，学生在解题的过程中检验自己对知识的掌握情况，并能够在课堂上查漏补缺.智慧课堂环境下将复习相关定义、公式、定理等内容前置，让课堂有更多的时间去解决重难点问题.

智慧课堂平台反馈学生作答情况，如图2所示，教师可根据学生的作答情况进行教学设计.另外，观察学生解题情况可以看出，大多数学生出错的地方位于第4题以及第8题.其中第8题是对有理项概念的不理解，稍作解释即可解决.而第4题是学生对二项式定理的推导方法不够理解.因此，课堂上以二项式定理内容以及应用作为重点进行突破.在课堂教学过程中，帮助学生进一步理解二项式定理的内容，以及推导定理的方法.

3.2  课中突破教学重难点，加深对二项式定理的理解

3.2.1  二项式定理知识结构图

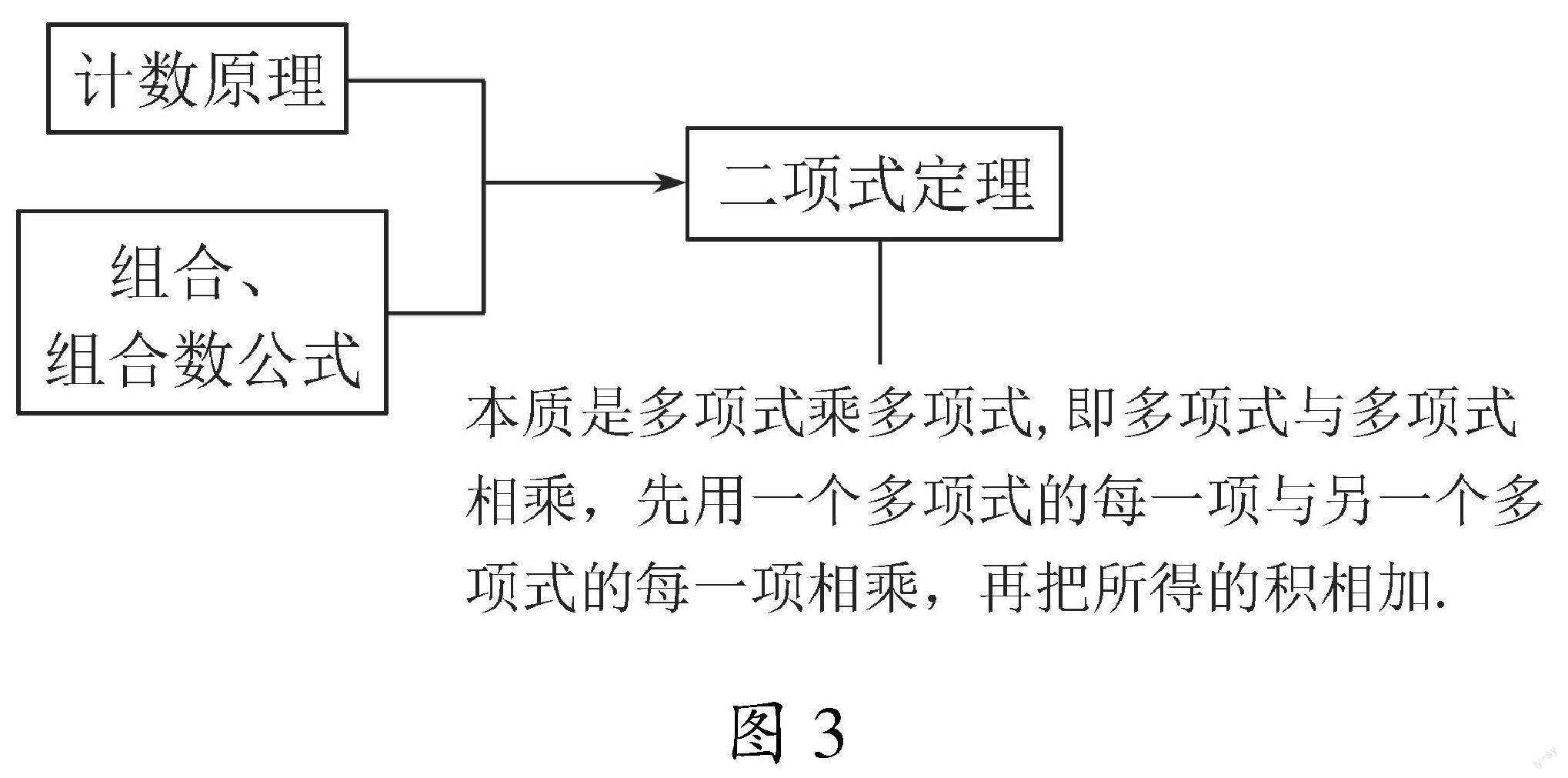
课件展示图3，让学生明确二项式定理内容，构建知识体系.

设计意图  知识是有结构的，知识的结构性在于知识内在的逻辑关系和外在的情境关联.知识结构化是一种必备的学习素养，在指导学生学习的过程中，教师要教会学生对知识的分析和理解，并在深刻理解的基础上建构起知识的内在关系和外在关联，培养学生的核心素养绝不是不重视知识的学习，但知识的学习拒绝碎片化和孤立化，我们需要有结构的知识的学习.知识的学习才是有意义的，我们也才可以在有意义的知识学习和建构中，直面现实问题的解决.

3.2.2  二项式定理的推导过程

课件展示二项式定理推导的微视频，扫码可以观看或下载，如图4.

设计意图  短短几分钟的视频内容，能够快速帮助学生回忆起二项式定理的推导过程，形象、直观、生动、省时，并以此突破本节课的学习内容.3.2.3  二项式定理例题讲解以及变式训练

题型1  求特定项的系数

题1：求（x2+3x+2）5展开式中的x的系数.

变式训练：（1）（1+2x）3（1－x）4展开式中含x2的项的系数是（  ）.

A.-5     B.-6     C.-7     D.-8

（2）（x-1）（x-2）（x-3）（x-4）（x-5）展开式中含x4的项的系数是（  ）.

A.-15     B.-120     C.15     D.30

设计意图  题1是课前作业的题目，可以向学生讲解三种解法.解法1是根据二项式定理的推导过程来求解；解法2可以将原式化为（x+1）5（x+2）5，然后利用二项式定理以及多项式乘多项式法则即可求出答案；解法3可以将原式化为［（x2+3x）+2］5，然后利用二项式定理的通项公式即可求出答案.通过三种解法让学生更为深刻地理解二项式定理的内容以及本质，并以此展开对后续题型的研究.题型2  公式的逆用

题2：化简C0n+C1n×6+C2n×62+…+Cnn×6n=.

变式训练：化简C1n+C2n×6+…+Cnn×6n－1=.

题型3  赋值法

题3：（2x+2）n各项系数之和为p，各项二项式系数之和为s，且p+s=272，求n的值.

变式训练：若x5=a0+a1（x+2）+a2（x+2）2+…+a5（x+2）5，则a0+a1+a2+…+a5=，a3=.題型4  系数单调性问题

题4：在（2x+1）10的展开式中，系数最大的项是，系数最小的项是.

变式训练：若2x2－1xn的展开式中有且仅有第五项的二项式系数最大，则展开式中系数最大的是（  ）.

A.第二项    B.第三项C.第四项    D.第五项

设计意图  题型2至题型4都是基于题型1展开的，层层深入主线，具有思考深度，运算量少，思想方法深刻，适合学生思考等特征.以这些题目进行课堂导学，避免难度过高挫伤学习积极性，或难度过低没有挑战性降低学生的成就感，学生在解答问题的过程中不断实现对知识体系的完整掌握.在智慧课堂的环境下，使得教师能够时刻把握全班同学的学习情况，最终达成教学目标.3.2.4  总结提升，课时评价

教师最后对本节课内容作出总结，课件给出以下思维导图，如图5，以及给出课时评价表，如表1，让学生对本节课内容作出合适的评价.

设计意图  教师在解决问题的基础上画出思维导图，意在帮助学生深度理解二项式的内容，避免因概念理解不清而解决不了问题.特别需要强调的是二项式系数与项的系数的区别，以及函数思想、赋值法等数学思想方法的渗透.

课时评价表，能让学生通过本节课的学习后，明确自己还有什么不足，后续要在哪方面继续努力.通过平台的数据统计功能，可以查看学生的评价情况，以便于教师作出教学反思.

3.3  课后分层作业，精准学习

课后可以根据平台对每个人的数据进行合理的作业推送，让学生形成自己的数学题库，智能推送分层作业，实现真正意义上的分层作业.教师也可以通过平台推送学习资源，以满足各个学生的不同需求.

4  教学感悟

智慧课堂平台可以提高学生的学习效率，让学生在智慧课堂的环境下主动地参与到学习中来，从而达到高效的学习.教师在上课前可以将所要讲解的知识通过平台分享给学生，学生可以根据需要做好笔记整理.还可以让学生提前预习知识，把不懂的问题记在平台上，通过这样的方式能够提高学习效率.学生在课堂上认真听讲、积极思考、认真记录，掌握了更多的知识.

老师可以利用平台的数据统计功能对学生的课堂情况进行了解，也可以及时向学生反馈课堂上的情况，这对于促进师生交流十分有帮助.

过去学生的学习资料基本以课本和练习册为主，学习途径较为单一.现在网络上具有丰富的教学资源，包括微视频、音频、图片、网页.教师可以有针对性地向学生共享资源，提高学生学习的热情，同时可以根据学习的需要进行下载，以满足每位学生的学习需求.作业是课堂教学的延伸和补充，是教学效果的重要评价依据.为了减轻学生负担，提高课堂效率，老师在布置作业时要进行分层作业.由平台的数据统计功能反馈学生的作答情况，可以让教师更为精准地进行帮扶工作，提升学生的学习成绩.

但需要清楚地认识到智慧课堂平台只是辅助工具，永远替代不了教师的引导作用.在上课前，教师需要对设备故障作出预案，不能出现唯有平台才能够上课的情况.另外教师也不能盲目地去使用，否则容易达成不了教学目标.最后，教师需要不断提升信息技术的水平，以实现技术与课堂教学的真正融合.

参考文献

［1］  中华人民共和国教育部制定. 普通高中数学课程标准［M］. 2版. 北京：人民教育出版社， 2020.5.

［2］  孙林林.基于智慧课堂的高中数学融合教学的实践思考［J］.中学数学教学参考，2022（19）：75-78.

［3］  文卫星. 如何上好期末复习课［J］. 中学数学教学参考， 2023（07）：1.

［4］  刘徽. 大概念教学：素养导向的单元整体设计［M］. 北京：教育科学出版社，2022：221-222.

作者简介  陈龙彬（1985—），广东新会人，中学一级教师；主要研究数学解题、数学教育；发表多篇文章.