充分联想，拓展思维，提高解题能力

辛爱群 朱记松

［摘  要］ 文章通过对2022年嘉兴、舟山中考数学压轴题的剖析，旨在引导学生充分联想相关知识点、基本图形，从不同角度进行深度思考，拓展学生思维的路径，提高学生分析问题、解决问题的能力.

［关键词］ 积累；联想；拓展思维；核心素养

试题呈现

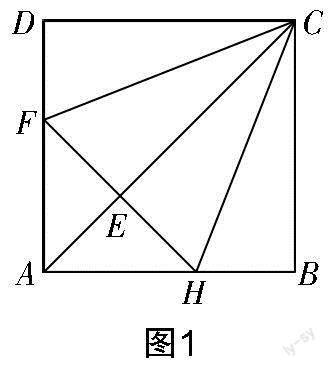
如图1所示，在正方形ABCD中，点F，H分别在边AD，AB上，连接AC，FH相交于点E，已知CF=CH.

（1）线段AC与FH垂直吗？请说明理由.

（3）如图3所示，在（2）的条件下，当点K是线段AC的中点时，求.

分析与简解

1. 问题（1）的分析与简解

根据已知条件，结合图形，联想正方形的性质，不难发现通过证明△DCF≌△BCH可得DF=BH，AF=AH，然后运用“等腰三角形‘三线合一”的性质得到AC⊥FH.

2. 问题（2）的分析与简解

要证明四条线段成比例，通常联想“三点定形法——证明四条线段所在的两个三角形相似”或“平行线分线段成比例定理及其推论”. 因为A，K，C三点在同一条直线上，所以不能直接证明两个三角形相似. 面对这一问题，常见的策略有三种：第一种，在“平行线分线段成比例定理及其推论”的启发下添加平行线构造“真A”型图形（如图4所示）；第二种，在图形中寻找或构造一条线段来替换KH，通过三角形相似来证明结论成立（如图5所示）；第三种，用三角函数表示AC，AK，HC，KH的长度，计算它们的比值证明结论成立. 因篇幅所限，这里仅根据上述三种策略列举三种方法，其他方法请读者自己探索.

方法1：如图4所示，过点K作KG∥AB交CH于点G，所以∠GKH=∠PHA，∠KGH=∠CHB.

因为四边形AHPF是☉E的内接四边形，所以∠DFC=∠AHP. 由问题（1）可知∠DFC=∠CHB，所以∠GKH=

3. 问题（3）的分析与简解

由于K是AC的中点（即为定点），所以图3中各线段的比值是确定的. 为探个究竟，不妨从下面两个角度进行思考.

第一，从作图的角度进行思考. 由问题（2）可知∠PHA=∠CHB，因此不难联想到构造△CHB关于AB的对称图形. 基于这个思路，解答如下：

第二，由中点联想三角形的中位线. 过点K作KM∥CH交AB于点M.因为K是AC的中点，所以M是AH的中点，AB=3BH，然后运用勾股定理、相似三角形的性质（或三角函数）表示CP，PF的长度，最后计算出它们的比值. 解答如下：

如图7所示，过点K作KM∥CH交AB于点M，连接KB. 由正方形ABCD的性质以及K是AC的中点，可得AK=KB，∠KAB=∠KBA=45°. 由问题（2）可知∠KMH=∠KHA，从而易证△AKH≌△BKM，于是AH=BM，得AM=BH. 由KM∥CH以及K是AC的中点，可知AM=MH=HB.

结合上述结论，下面给出两种方法.

解题反思

1. 考查“四基”

该题是该卷的压轴题，突出考查基本知识、基本技能、基本数学思想、基本解题经验，难易适中，能够助力义务教育提质增效. 具体来说，该题以正方形、共顶点的等腰直角三角形为背景，设计三个问题，着力考查正方形、等腰（直角）三角形、全等三角形、三角形中位线定理、相似三角形、勾股定理、锐角三角函数、圆的基本性质、计算与推理能力以及转化思想等，具有较强的综合性和灵活性（问题（2）的解法多样），各小题呈递进关系，由易到难，层次分明，具有较强的区分度，在确保中考选拔功能的基础上，能有效考查不同层次学生的数学基础知识、基本技能和数学思想.

2. 聚焦核心素养

教学启示

1. 解题需要原始积累

皮亚杰的认知建构理论要求教师在平时教学中，重视学生头脑中原有知识和经验的作用，重视学生在学习活动中的主观能动性. 《义务教育数学课程标准（2022年版）》也强调，数学活动经验的积累是提高学生数学素养的重要标志. 因此，在平时教学中，教师要引导学生通过作数学笔记、写数学日记、解题反思、自主复习等行为养成良好的学习习惯，以促进学生积累数学知识、数学思想、解题方法、解题经验（策略）、基本图形、基本题型和基本结论，帮助学生完善认知结构，自主构建认知体系.

2. 解题需要充分联想

聯想是指由于某人或某事物而想起其他相关的人或事物；由于某概念而引起其他相关的概念. 联想是解题的关键，在数学解题中，可以由已知条件联想到相关的知识点、定义、定理；由结论联想到相关的基本图形、基本结论或要得到结论所需要的条件和可能的方法.

3. 解题需要“学科一般观念”的指导

章建跃博士指出：“学科一般观念是指对本学科学习和研究具有广泛、持久、深刻影响的基本数学思想方法和基本思维策略方法，是数学研究的方法论，对学生用数学来观察和分析世界，提出并解决问题具有指路明灯的作用.” 笔者窃以为：数学解题教学，教师应潜移默化地培养学生形成有效的解题思维策略（思维过程如图8所示），培养学生的审题意识，在认真审题的基础上，通过充分联想、类比，唤醒已有的解题经验，建立条件与结论以及前后小题间的联系，制定解题方案，优化解题方法，最后总结反思，形成新的经验，提高解题能力.