运用问题链，发展高阶思维

陈嘉尧

［摘  要］ 高阶思维的培养是落实核心素养的重要途径. 数学课是思维培养的主阵地，而问题是高阶思维发展的最大动力. 文章以“图形的位似”的教学设计为例，对比常规课堂教学，设计指向“问题链教学”，探索运用递进式问题链、评价式问题链、发散式问题链发展学生分析、评价、创造等高阶思维的有效途径.

［关键词］ 高阶思维；问题链；图形的位似

引言

高阶思维研究源于布鲁姆和加涅的认知水平分类：识记、理解、运用为低阶思维，分析、评价和创造为高阶思维［1］. 发展学生高阶思维的最基本途径是解决问题，包含学生学习问题解决方法与教师教学问题解决方法两方面.

传统的“单一问题”不足以满足学生“层进式”学习知识的需要，进而发展基于“单一问题”，由“延伸问题”所构成的问题链，有效促进学生对内在结构逐层深化的知识的学习，但仍难以发展学生的高阶思维.

问题链不是几个问题的简单叠加，而是有目的性、系统性、层进性的问题组，指向问题解决的问题链包含起始问题，延伸问题，提炼问题三部分［2］（如图1所示）. 教师应根据数学学科的特点，基于发展性的课程知识观去构建大问题背景，以起始问题对接教学切入点，以延伸问题为学科核心思想方法构建脉络，以提炼问题为学生提供思考与表达的空间. 本文以北师大版教材九年级上册第三章第8节“图形的位似”为例，展示如何运用问题链发展学生的高阶思维.

常规教学设计

问题1：如图2所示，五幅图片是形状相同的图形，取图中相对应的两点A，B，它们的连线经过镜头中心P吗？换其他的对应点试一试，还有类似规律吗？

问题2：如图3所示，两个相似五边形，设直线AA′与BB′相交于点O，那么直线CC′，DD′，EE′是否也都经过点O？

师生互动：归纳位似多边形的定义以及位似中心的定义.

探究：测量并计算，①对应点到交点O的距离之比；②对应边的相似比.

师生互动：总结位似多边形的特点和性质，得到位似多边形对应顶点到位似中心的比等于相似比.

以上是某教师参加“一师一优课，一课一名师”活动获得的部级优课的教学设计，学生在教师指导下经历了观察、测量、运算、猜想、归纳等数学过程. 但在教师过多的“预设”下，呈现的活动过程近似假活动. 学生虽亲历了问题的“探究”过程，但面对“已知”（教师已呈现探究目标）目的或结论的“数学问题”时，所谓的观察、测量、运算、猜想等都是较低思维水平的活动，难以达成学生对内在结构逐层深化的知识的学习.

基于问题链的教学设计

叶圣陶先生说过“教是为了不教”. 因此，教师在传给学生知识内容的同时，更应授给学生学好数学的方法. 数学问题链教学通过构建思维型问题，在内容上引导学生进行更深层次的数学学习，激发学生多元思考和探索，进而让学生在思考方式、方法、路径和策略上有所收获，体悟关键方法与核心思想. 比较人教版、北师大版教材呈现的位似定义，发现人教版更多是从几何直观到位置关系的刻画，而北师大版则是从数量到位置关系的刻画. 基于教材特性，在执教北师大版教材中的“图形的位似”这节内容时，可以借鉴人教版教材的亮点，在教学过程中利用问题链引导学生先经历几何直观下的感性认识，再经历数量刻画下的理性认识.在此过程中，不仅要重视数学定理的形成，也要追求对“数学定理”的修改、优化.

1. 展开递进式问题链，发展分析高阶思维

起始问题1：前面我们学习了图形的哪些变换？

延伸问题1：三种几何变换（旋转、平移、翻折）前后，图形全等. 迄今为止，还未学一种变换能将图形放大或缩小. 生活中有哪些你熟悉的能将图形放大或者缩小的实例？

延伸问题2：刚刚所举实例中，哪些例子有共性？

延伸问题3：老师在拖动图形的过程中，你观察到了哪些现象？

延伸问题4：什么是相似多边形？相似多边形有哪些性质？

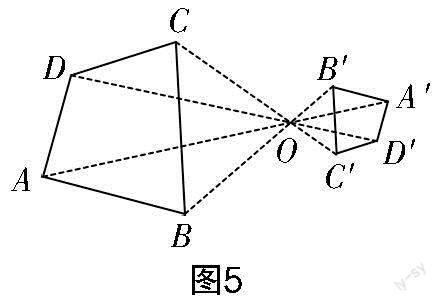
延伸问题5：（如图4、图5所示）我们继续观察，这两组放大或缩小的图形有哪些共性？

延伸问题6：这里的对应点有几对？应该如何描述？

提炼问题：如果两个相似多邊形任意一组对应顶点所在的直线都经过同一点O，而且对应边互相平行，那么这样的两个多边形叫位似多边形（记为“判定1”）. 点O称为位似中心.

设计意图  从图形变换的角度进行研究，可以将位似与中心对称进行对比；从图形性质的角度进行观察，可以将位似与相似进行类比. 因此，这里围绕起始问题1设计了一系列递进式问题，意在帮助学生借助几何直观，得到位似多边形的一种判定方法. 在此过程中，根据学生的认知水平循序渐进地指引学生思考，得到位似多边形的“判定1”，渗透数学学科的一般学习方法，培养学生的几何直观和逻辑推理素养，发展学生的分析高阶思维.

2. 拓展发散式问题链，发展创造高阶思维

起始问题2：我们除了研究位置关系外，还研究过什么？

延伸问题1：与一般的相似多边形相比，我们的位似多变形多出了位似中心. 你以前学过哪些与“中心”相关的知识？

延伸问题2：图形旋转中与旋转中心相关联的性质是哪一条？

延伸问题3：（我们总说，全等是特殊的相似）从相似的角度来看，这句话（对应点到旋转中心的距离相等）还可以怎么描述？

延伸问题4：我们可以作何猜想？

延伸问题5：借助图6，你能证明猜想吗？

提炼问题：对应点到位似中心的距离之比为定值.

设计意图  在图4、图5中，（用几何画板演示）当OB=OB′时，四边形ABCD与四边形A′B′C′D全等，将此作为起始位置进行拖动，有利于学生将位似与中心对称进行对比，发散思维，从而顺利猜想出位似多边形的数量关系. 因此，这里围绕起始问题2设计了一系列发散式问题，基于简单的、学生已解决的问题（由几何直观得到的位似多边形的性质），启发学生“自己发现”位似多边形的性质，再引导学生从已有的位似性质、判定1猜想出判定2.在此过程中，促进学生对数学知识认知的深化与提高，发展学生的创造高阶思维.

3. 深化评价式问题链，发展评价高阶思维

起始问题3：你能根据位似多边形的性质，推测出位似多边形的其他判定方法吗？

延伸问题1：请同学们思考并说明“判定2”是否正确.

延伸问题2：对于两条判定方法，你觉得哪条更好？

延伸问题3：在刚才的学习过程中，同学们还有其他发现、推测、质疑吗？

提炼问题：如果两个相似多边形任意一组对应顶点所在的直线都经过同一点O，而且任意一组对应顶点到位似中心O的距离之比为定值，那么这样的两个多边形叫位似多边形（记为“判定2”）.

设计意图  这里围绕起始问题3设计了一系列评价式问题，意在引导学生遵循几何学习一般的路径. 通过延伸问题1，启发、引导学生从已有的位似性质、判定1猜想出判定2，并加以证明，培养学生的逻辑推理能力；紧接着通过延伸问题2，促使学生在对比过程中加深对新知识的理解和应用，发展学生的评价高阶思维；最后设置延伸问题3，意在渗透发展性的课程知识观，促进学生对数学知识认知的深化与提高，发展学生的创造高阶思维.

教学反思

关于“图形的位似”这一节内容，在以中考为目标的教学中，往往形同“鸡肋”：食之无味，弃之可惜. 中考基本上不考，但作为考试大纲的内容之一，又不能不教. 因此，教师应该在知识“无味”的前提下，去挖掘这一教材的其他教學价值！基于“价值”导向，笔者有几点看法.

1. 基于大问题背景，深度理解知识

问题是教师教学与学生学习的灵魂. 基于大问题背景设置的问题链指向结构化的数学知识，指向发展性的课程知识观. 教师要充分发挥数学学科独特的育人价值，用问题引领课堂，帮助学生主动建构知识体系，形成良好的认知结构，积累解决问题的策略，改变思维方式，最终实现思维品质的提升. 例如本节课的教学设计，以三个具有目的性的大问题（起始问题）引领的问题链贯穿课堂. 教师先用几何画板通过动态演示，引导学生直观感受具有特殊位置关系的相似图形；然后借助递进式问题归纳概括“位似”的“定义”（即判定1），凭借发散式问题猜想一般位似多边形的性质，运用评价式问题对比两个判定方法的优劣，加深对新知识的理解应用；最后通过课堂留白，激发学生课后探究、深思的热情，实现思维碰撞灵动［3］.

2. 运用问题链，发展高阶思维

问题链具有开放性、发展性、探究性等特点［4］. 在课堂教学中，利用具有不同教学功能的问题链，有助于学生在拓宽和优化知识结构的过程中，感悟数学的整体性、思想的一致性、方法的普适性. 例如本节课的教学设计，三个起始问题可谓环环相扣，每一个起始问题下的一系列延伸问题又相辅相成，有效引导学生感悟数学思维方式，渗透从特殊到一般的数学思想方法，实现学生对新旧知识的整合、建构、升华，深度理解数学知识的本质，达成几何直观、逻辑推理两大数学素养落地. 在基于高阶思维培养的问题链教学中，展开递进式问题，发展学生的分析高阶思维；拓展发散式问题，发展学生的创造高阶思维；深化评价式问题，发展学生的评价高阶思维！

3. 树立发展性的课程知识观，培养学生的远见卓识

深度学习倡导：要追寻知识的广度、深度和关联度. 因此，新时代的数学教育应着眼于学生的发展，着眼于学生的未来. 基于学生远见卓识的培养，教师应树立发展性的课程知识观，努力去发现具备研究价值的问题，设计成可供探究的问题链，激起学生学习数学的热情，勾起学生探求数学的好奇心，促进学生深度思考. 在此过程中，需要教师用高观点去指导学生的数学学习与探究活动，帮助学生主动建构知识体系，形成良好的认知结构，促进学生数学思想的升华和思维能力的发展，实现从“知其然”到“知其所以然”再到“知何由以知其所以然”的跨越.

参考文献：

［1］洛林·W. 安德森. 布鲁姆教育目标分类学：分类学视角下的学与教及其测评［M］. 北京： 外语教学与研究出版社，2009.

［2］唐恒钧，张维忠， 陈碧芬. 基于深度理解的问题链教学［J］. 教育发展研究，2020（04）：53-57.

［3］陈海烽. 灵动课堂：从传授知识到传递智慧［M］. 西安：陕西师范大学出版总社，2018.

［4］黄光荣. 问题链方法与数学思维［J］.数学教育学报，2003，12（02）：35-37.