数学理解视角下数学史的价值与选取原则

黄贤明 徐敬元

［摘  要］ 数学理解是国际数学教育研究的热门话题之一，数学史在数学理解的过程中也发挥着重要作用. 文章通过对数学理解的内涵及特征的分析，指出数学史与数学理解的关系，揭示数学史对于数学理解的价值是“解释知识之源、促进意义构建、推动迁移应用和奠定文化理解”，并提出数学史的选取应遵循启发性、探索性和深刻性原则.

［关键词］ 数学理解；数学史；选取原则

理解是教育永恒的追求. 20世纪90年代以来，“学习经济”与“终身学习”得到国际社会的广泛认同，有效学习的理念也逐渐从“记忆与练习”转向“理解与应用”. 学习者必须拥有对复杂概念的深层次理解能力，并能将其应用于生成新的知识、新的观点、新的理论等［1］. 自此，“为理解而教，为理解而学”的教育理念成为当代教育改革的重要思潮. 在数学教育领域，数学理解一直是人们关注的重点，与问题解决并列为国际数学教育研究的两大主题. 在已有的研究中，人们已经重点探讨了数学理解的内涵、数学理解的价值意义、数学理解的过程模型、数学理解的实现等问题，其中皮瑞和基伦深入研究了数学理解的增长趋势与表征，构建了“超回归”数学理解模型，提出了数学理解的八个水平，对后续数学理解的研究产生了深远影响. 对于数学理解的实现问题的探讨，研究者的观点不尽相同，有的研究强调教师在课堂教学中的主导作用，有的研究则关注数学交流、数学实验在数学理解中的价值……随着国内HPM研究的深入，数学史“知识之谐、文化之魅、方法之美、探究之乐、德育之效”的教育价值不断凸显，基于数学史的教学课例不断开发，数学史亦受到了广泛关注［2］. 自然，数学史在教学中的渗透也将在一定程度上促进数学理解，即数学史在数学理解的实现中也拥有不容忽视的作用与价值. 但目前很少有研究者从数学史的视角下探索数学理解的实现，HPM研究与数学理解的研究处于相对独立的状态. 鉴于此，本研究尝试探索数学史在数学理解中的作用，构建数学史与数学理解的关系，并在数学史五大选取原则上阐述指向数学理解的数学史选取新原则.

数学理解的理论框架

1. 从理解到数学理解

“理解”在《辞海》中被定义为：“了解、领会. 是通过揭露事物间的联系而认识新事物的过程. ”而《义务教育数学课程标准（2022年版）》（以下简称《标准》）则将“理解”作为描述目标的行为动词，解释为：“描述对象的由来、内涵和特征，阐述此对象与相关对象之间的区别和联系.［3］”理解是一个较难界定的概念，不同学科流派也会产生截然不同的认识. 从哲学的角度来看，理解最早源于对古代文化的解释. 随着人们对“理解”问题的探索，理解最终被视为人的交往实践活动，强调理解的创造性和主体性，关注理解的多元性和差异性. 从认知心理学的角度来看，理解本质上是学习者以信息的传输、编码为基础，根据对已有信息建构内部的心理表征，获得心理意义的过程［4］. 从脑科学的角度来看，理解是学习者在浸润性地主动参与动态的、整体性的、实践性的知识的建构，即以整体、浸润、联系的观点来解释理解.

“数学理解”区别于一般的“理解”，它是对数学知识、数学思想等的理解，研究者对其内涵的解释也各具特色，具体从以下三个角度进行说明：一是网络联系的角度，数学理解是指数学对象被纳入学习者的内部表征网络，即学习者将新知识与已有知识建立联结，使之纳入学习者头脑中的知识网络，进一步丰富、完善网络结构. 二是表征转化的角度，数学理解是指用不同的方式表征数学对象，并实现表征方式相互转化的能力. 在表征方式相互转化的过程中，学习者需重新解释和建构数学对象，获得对数学对象的新认识，形成深刻的理解. 三是类型层次的角度，斯根普提出工具性理解和关系性理解的分类，并指出数学教学的最终目标是使学生获得关系性理解. 研究者在此基础上提出了理解的四面体模型，即数学理解可以划分为直观理解、程序理解、抽象理解和形式理解，诠释了数学理解的多样性、过程性等特点.

2. 数学理解的特征

从数学理解的内涵中不难发现，数学理解拥有以下几个特征.

其一，数学理解是集过程与结果于一体的概念. 这意味着数学理解既是一个动态、连续、螺旋式发展的过程，也是经历数学理解性学习后所达成的对数学对象的理解结果. 从过程来看，数学理解是从浅层理解出发，在一系列外部刺激的作用下，逐渐形成对数学知识的深层理解的过程. 从结果来看，数学理解是指学习者表露出来的对数学知识提取、应用的能力，所谓数学理解的达成就是学习者能够准确描述数学对象的内涵、区别、联系，形成数学对象的知识网络，并能够随时将其应用于问题的发现与解决.

其二，数学理解的本质在于建立联结. 其既是建立新旧知识联系的过程，从而形成数学知识网络；又是建立联结、知识纳入网络的结果，即达成了关系性理解，从而表露出将数学对象的不同表征方式相互转化的能力.

其三，数学理解拥有不同的水平层次. 对于相同的数学知识，受限于不同学习者的理解能力、学习习惯等因素，所获得的数学理解也是参差不齐的. 具体来说，可以分为记忆性理解水平、解释性理解水平和探究性理解水平［5］，高水平层次的数学理解是数学教育所追求的目标.

3. 数学理解与数学史的关系

数学理解与数学史既相互独立又相互联系. 第一，数学史是实现数学理解的重要手段. 数学史正如“使面包和黄油更加可口的蜂蜜”，使数学学习更具有吸引力［6］，其教育价值不言而喻. 因此，数学史不仅要在课堂教学中有所渗透，在教材、习题、考试中也应该有所体现. 在知识理解的过程中，数学史的加入能够有效解决“知识何来源”“知識何价值”“知识何应用”等疑惑，构建学生对知识意义的理解，同时也能够激发学生的探索兴趣，促使学生文化性理解的形成. 第二，数学理解必将促进学生对数学史的探索. 数学理解的实现是多种因素相互作用而达成的结果，学生的好奇心与求知欲将不断驱动他们探索知识及其相关内容，包括对知识背后数学史的理解. 第三，数学理解与数学史在数学教学中是相互制约、相互引导、相互促进的. 在数学理解的过程中总会存在一些只能通过数学史来回答的问题，如“‘函数一词是怎么来的？”“无理数是‘没有道理的数吗？”等等. 当然，学生的数学理解水平会影响他们对数学史的认识与理解. 因此，在数学教学中要把握好数学理解与数学史的关系，巧妙地将数学史渗透于数学理解的始终，使其更好地为数学理解的实现而服务.

数学史对数学理解的价值

1. 解释知识之源

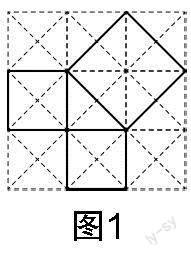
学生对于数学知识的理解往往是一种经验性理解，即源于学生已有认知或生活经验的对数学知识表层的、不全面的、主观的，甚至错误的理解與认识，是学生知识理解道路的起点. 学生的学习困难具有历史的相似性，数学史恰巧可以承担起学生理解道路中“指明灯”的角色，解决“知识何源”的问题. 例如，勾股定理最早可能是由毕达哥拉斯在观察等腰直角三角形拼成的地砖中发现的. 在教学中，教师就可以创设相似情境，呈现图1，让学生在观察中发现勾股定理的雏形，得到相关假设并加以验证. 在这个过程中，可以充分调动学生的经验性理解，阐述勾股定理的来源，并有效推动勾股定理的探索进程，促进学生对勾股定理的理解.

2. 促进意义构建

在《标准》的课程内容中，经常会出现“理解……的意义”的要求，如“理解负数的意义”“能根据现实情境理解方程的意义”等. 那何为“理解知识的意义”呢？这是在理解数学知识本质的基础上，还要理解其产生的意义和学习的意义，乃至对数学学科价值的理解，属于数学理解的重要一环. 数学知识的意义并非无源之水、无根之木，需要以历史的视角来审视，整体构建知识的多种意义，以此促进学生对数学的理解. 以韦达定理的教学为例，大多数教材都选择用求根公式来求证韦达定理，这种方法虽然简便、直观、易于理解，但其恰恰忽视了对韦达定理的意义的构建. 求根公式的实质就是用一元二次方程的系数来表示方程的根，也就是说学生已经掌握了根与方程系数的具体关系，那为何还要学习两根和、两根积与系数的关系呢？再加上初中阶段对韦达定理的应用较少，这不禁让学生质疑韦达定理的意义，进而阻碍学生深入理解. 从历史上看，韦达定理最早可以追溯到16世纪，其证明方法大多围绕的是“设而不求”思想，如吉拉尔的代入相减法、欧拉的因式分解法等. 直到19世纪，华里斯才运用韦达定理得到了求根公式. 因此，教学中可以选取较为复杂的一元二次方程（如系数过大的一元二次方程）用于学生感受求根公式的“失效”，进而引出韦达定理，并利用历史上的方法加以证明，最后设置用韦达定理证明求根公式的环节，促使学生建立韦达定理与求根公式之间的联结，达成对韦达定理的意义的理解.

3. 推动迁移应用

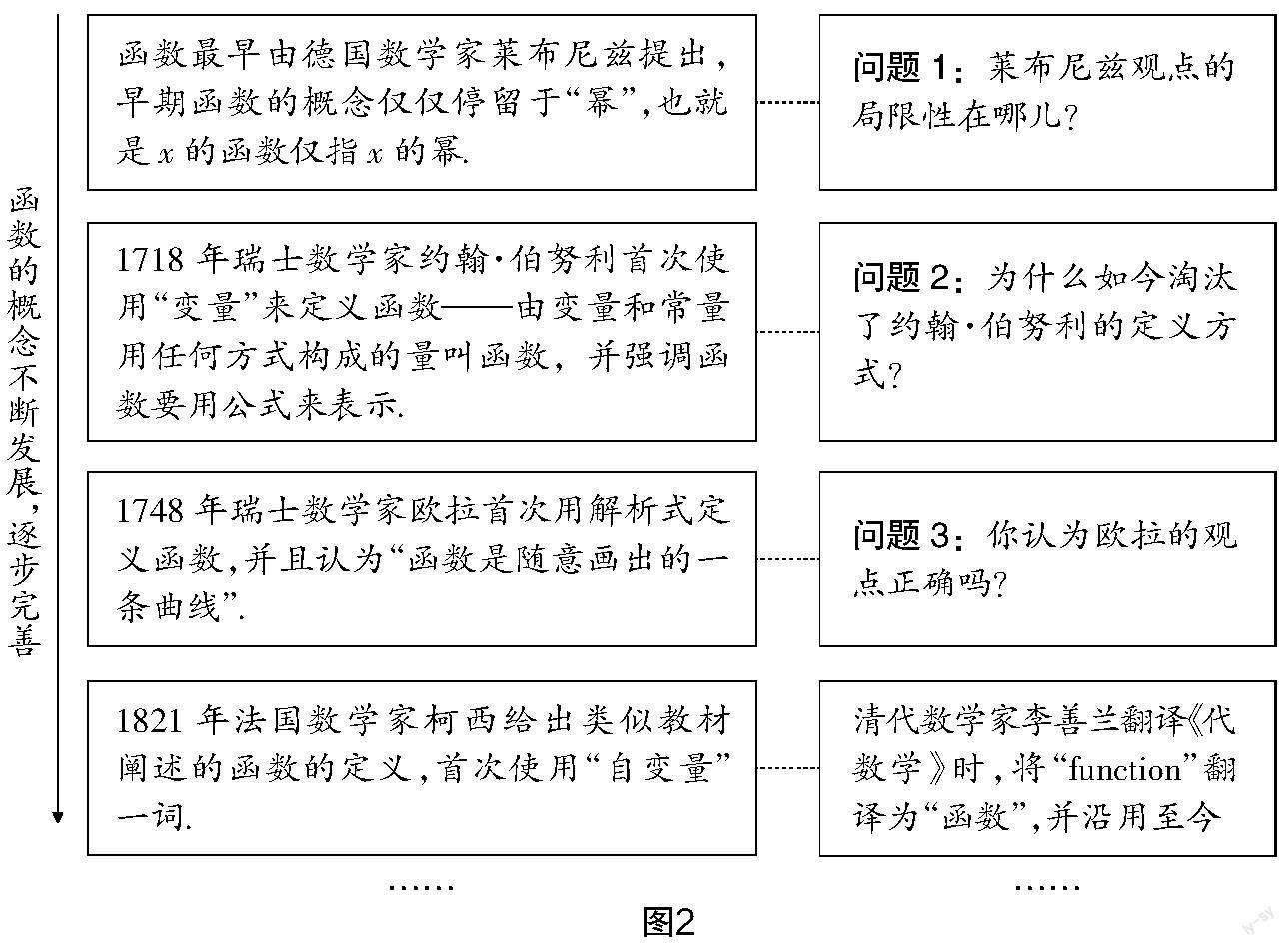
迁移性理解是指将知识应用于陌生的情境中解决相关问题的过程，是在数学理解过程中检测学生数学理解水平的重要阶段，也诠释了数学理解的价值意义. 数学史在此阶段充当着“素材库”的作用，教师可以选择相关数学史料作为背景设计相关试题，以达到检测学生的数学理解水平，促使学生迁移应用知识的目的. 例如，在初中函数概念的教学中，教师可以围绕函数概念的发展历史设计问题（如图2所示），引导学生思考历史上的数学家所定义的函数存在的缺陷，将如今的函数概念与历史上的函数概念作对比，进一步加深对函数概念的理解. 当然，《九章算术》《几何原本》等数学专著中的数学问题及其改编题也能在教学中达到相应的目的.

4. 奠基文化理解

数学史是数学文化的有机组成部分，也是数学教学不可或缺的内容. 在知识理解中，文化性理解贯穿数学理解始终，为数学理解的各个环节提供着源源不断的“能量”. 文化性理解是立足知识本身，并追溯到知识背后所隐藏的发展脉络、名人轶事、思想方法等，形成学生独特的数学文化体系. 数学史的加入能够在学生心里埋下一颗“文化的种子”，这颗“种子”将会在学生后续知识的学习中生根发芽，长成一棵参天大树. 例如，学生在七年级学习负数等内容时，教师可以渗透中西方关于负数的历史，引导学生自主思考西方为何不接受负数等问题，捋清负数的发展脉络. 而后随着学习的深入，在探索一元二次方程的几何解法时学生就会意识到，西方数学家更倾向于在直观的几何中找到对数学的解释，比如几何解法只能表示正根. 此时，学生对数学的理解不再停留于知识本身，而是在此基础上以整体的视角构建一种文化理解观，达到较高水平的数学理解.

指向数学理解的数学史选取原则

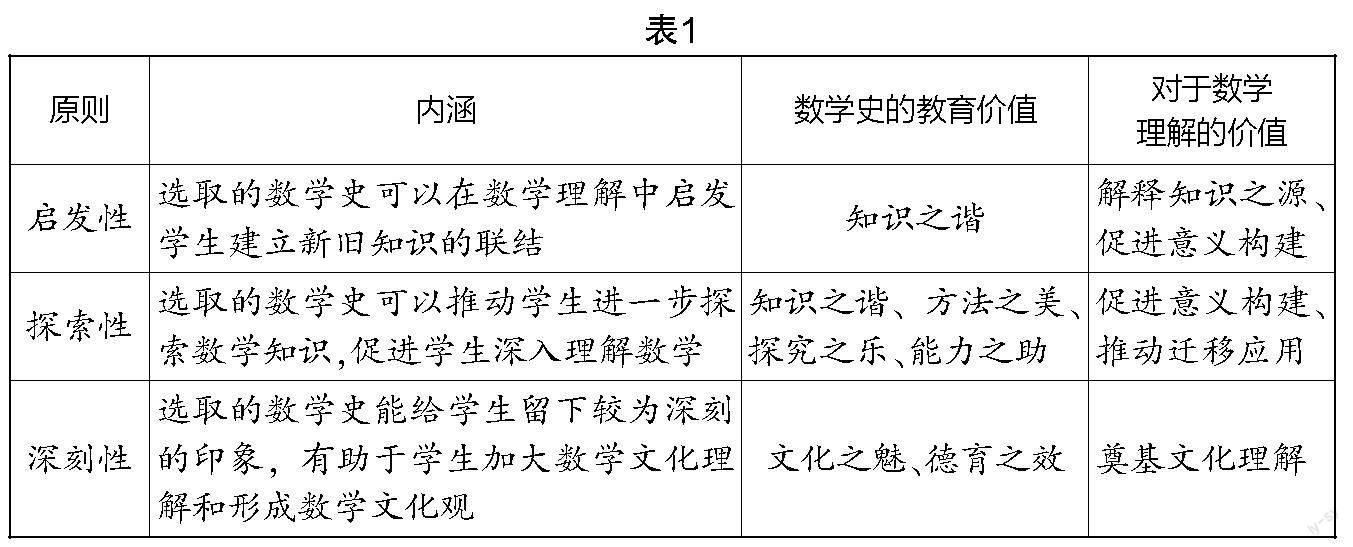
从已有研究来看，数学史的选取要遵循“趣味性、可学性、有效性、人文性和科学性”五大原则，这是数学史选取的基本原则［2］. 在指向数学理解的视角下，数学史不能如蜻蜓点水般地简单罗列，而要在“好”中取“精”，选择最适合帮助学生达成数学理解的史料. 因此，数学史的选取原则应有所补充——加入启发性、探索性和深刻性原则，具体见表1.

在指向数学理解的数学史的选取中，首先要遵循启发性和探索性原则，做到让数学史为推动数学理解的实现而服务，既帮助学生激活旧知、激发求知欲，又有效推进学生深入数学理解. 其次，以深刻性原则保证数学史呈现的有效性，以期学生通过所呈现的数学史获得对数学知识更为全面的理解，这种理解包括知识背后的历史文化等内容，进而激发学生自主探索的欲望. 当然，深刻性也可以是数学史料中的德育、美育等因素对学生留下的深刻印象.

结语

数学史在数学理解的实现中发挥着重要作用，指向数学理解的教学自然也离不开相关数学史的融入. 在数学理解实现的道路中，教师要关注理解过程，聚焦理解本质，明晰理解目标，在五大原则的基础上以启发性、探索性和深刻性原则选取史料，并在恰当的教学环节中展示出来，以此促进数学理解的实现.

参考文献：

［1］徐兆洋. 为理解而设计教学：原理与方法［M］. 广州：世界图书出版广东有限公司，2017.

［2］陈晏蓉，汪晓勤. 数学史料的选取原则与案例分析［J］. 教育研究与评论（中学教育教学），2017（12）：37-43.

［3］中华人民共和国教育部. 义务教育数学课程标准（2022年版）［M］. 北京：北京师范大学出版社，2022.

［4］毕力格图，史宁中，马云鹏. 基于数学教育观的“理解”之理解［J］. 东北师大学报（哲学社会科学版），2011（02）：159-163.

［5］徐彦辉. 初中生数学理解水平的测试调查研究［J］. 数学教育学报，2012，21（02）：26-28+66.

［6］黄贤明. 数学史渗透数学教学的微思考——以“有理数”单元为例［J］. 中学数学月刊，2022（06）：49-51.