专题教学：让问题在对话追问中渐次展现

杨晨

［摘  要］ 围绕某一道难题（比如“圆币滚动”问题）教学，如果只是“就题讲题”，那么过一段时间学生就会遗忘；如果先找出这道难题的一些同类题，并将它们改编为题组，每一个题组下的系列问题伴随着教学进程渐次展現，那么学生在一题多变、多题归一的专题教学中就能掌握一类问题的解答策略，悟透这类问题的深层结构.

［关键词］ 专题教学；圆币滚动；对话追问

在本校最近一次九年级期中考试的试卷中，有一道得分率很低的填空题：

将两枚同样大小的圆币放在桌上，固定其中一枚，而另一枚则沿着其边缘滚动一周，这时滚动的硬币滚动了_____圈.

很多学生表示这道题无从入手，不会思考. 为此，笔者在中国知网中检索相关文献［1］，受其启发，围绕“圆币滚动问题”研制了一节专题课，以期帮助学生想深、学透这类问题.

“圆币滚动”专题课教学设计

教学环节一：初步感知

问题1  如图1所示，设直径为1的圆形硬币放在原点，将硬币沿着数轴滚动一周，点A到达点A′的位置，则点A′表示的数是几？

教学组织：这是不同版本教材上都出现过的一个素材，引导学生回顾点A′表示的数是无理数——圆周率π. （继续追问与变式）

追问：画图分析，圆形硬币滚动一周，其圆心所经过的路径的长度.

预设：构造图2可得圆形硬币的圆心所经过的路径的长度为线段O1O2的长度，恰为圆形硬币的周长π.

变式：图3、图4、图5中的☉O均做无滑动滚动，☉O的周长为2π.

（1）如图3所示，∠ABC=90°，AB=BC=π，☉O从☉O1的位置出发，在∠ABC的外部沿A→B→C滚动到☉O4的位置，分析☉O自转几周.

（2）如图4所示，△ABC的周长为3π，☉O从与AB相切的点D的位置出发，在△ABC的边上沿A→B→C滚动，当☉O回到出发位置时，分析☉O自转几周.

教学环节二：变式探究

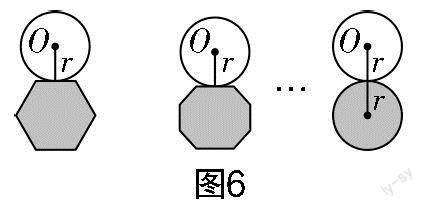
问题2  在图6中的系列图形中，半径为r的圆在周长为l的多边形的外部顺时针平滑滚动，回到出发位置时圆自转多少周？

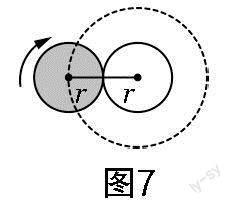
变式：（1）如图8所示，小圆绕直径4倍大的圆滚动一周，回到原处，小圆滚动了几圈？

（2）如图9所示，☉O1的半径是☉O2的半径的2倍，☉O1沿☉O2的周围平滑滚动，回到原来位置时，☉O1滚动了几圈？

教学组织：学生根据示意图可知，只要求出☉O1的圆心所经过的路径的长度（如图8、图9中的虚线圆，其周长分别为10πr和6πr），再分别除以☉O1的周长（分别为2πr和4πr），即得它们分别滚动了多少圈（分别为5圈和1.5圈）.

教学环节三：拓展提升

问题3  如图10所示，将4枚半径为1的圆币放在桌上，固定其中3枚（白色圆币），另一枚（灰色圆币）沿着它们的边缘从☉O滚动到☉O′的位置，☉O滚动了几圈？

教学环节四：课堂小结

小结问题1：本节课主要研究“圆币滚动问题”，你对哪道习题有较深的印象，请在小组内分享各自的理解.

小结问题2：分析一些比较复杂的“圆币滚动问题”，常常会出现一些易错点，你在这节课中有没有“出错”经历？如果有，请把你的“出错”经历整理出来跟大家分享；如果没有，说说你防止“出错”有怎样的经验.

教学立意的进一步阐释

第一，聚焦主线，开展深度解题教学

专题复习课的备课选题是关键，所选习题一定要确保选题的“内容效度”［2］聚焦主线. 以上述课例中的问题、变式或拓展来看，笔者对“原题”进行了深度改编，比如原题中的一些问题与本节课的训练主线不太一致，就进行了删减，让所有问题紧紧围绕“圆币滚动”而展开. 学生通过训练后，对这类问题有了更加深刻的理解. 关于追求有深度的解题教学，主要是相对于零散出现的个别难题而言. 具体来说，如果有些难题在日常练习或讲评中“就题讲题”，那么过一段时间学生就会遗忘；而如果围绕一类难题同类跟进、变式再练、举一反三、多解归一，那么过一段较长时间学生再遇到时，还是能识别出来并成功解决.

第二，问题驱动，渐次展开彰显关联

在专题教学中，当选定一些同类习题后，如果对这些同类习题进行必要的改编，使之成为驱动专题教学的“问题”，可彰显教师的专业基本功. 一般来说，需要将入选的同类习题进行由易到难的排序，比如将较易的同类习题设置为“问题1”而出示，组织“问题1”的教学时，相机出示“变式”，但难度要控制，即学生不动笔、稍加思考就能得到思路. 在“问题1”之后拾级而上，安排“问题2”及变式，这个环节是全课的重点，要求全员思考，力争全员学会. 在“问题3”的题组中，设置较难习题进行探究，考虑到课堂时间有限，先安排学生独立思考，让获得思路的学生上台交流，分享他们的解答过程，再请一些平时水平一般的学生复述思路、反馈学情.

第三，对话追问，切实体现“学为中心”

基于课前精心选编的“问题”驱动教学进程，要重视对话追问，在师生对话、生生对话中渐次出现系列问题，让学生感受到问题的出现是自然而然的，体现“学为中心”的教学理念. 具体来说，当“问题”的题干出示后，有时并不急于设问，可以先问一问学生能提出怎样的问题. 当学生提出问题后，大家再一起求解. 如果学生提出的问题不严谨或有错漏，可以安排全班学生参与完善与优化. 这种开放式的教学可以有效激发学生参与课堂的兴趣.

第四，解后回顾，小结问题反思提炼

专题课要重视课堂小结环节，要通过课前精心准备的“小结问题”引导学生回顾反思. 这里所指的“小结问题”一定要精准针对本课所学内容，而不是那种“空、泛”式的小结导语，如“这节课你学到了什么？”“这节课你感悟到了哪些数学思想方法？”. 以本节课中的“小结问题”为例，让学生选出一道自己印象最深的问题，实则让学生回顾本节课所学的全部内容. 可见，这个小结问题达到了引导学生回顾本节课所学内容的教学目的.

参考文献：

［1］李传富. 多角度探究一道硬币自转问题［J］. 中学数学，2016（02）：87-89.

［2］邓厚波. 内容效度：章末试卷命制的关键指标——以人教七下“实数”章末检测命题为例［J］. 中学数学，2019（10）：70-71.