数学运算素养的水平划分与评价

李瑛 沈婕 刘勇 王洪亮 谭毅

[摘要]以2022年高考数学（天津卷）实测数据为依据，参照《普通高中数学课程标准》核心素养水平划分标准，分析考生数学运算素养的发展情况，并针对考生在数学运算素养方面表现出的问题，从明晰运算对象、掌握运算法则、选择运算路径、求得运算结果四个方面对高中数学教学提出建议。

[关键词]核心素养；数学运算素养；水平划分；评价

[中图分类号]G424.74[文献标识码]A

[文章编号]1673—1654（2023）02—001—012

本文为教育部教育考试院“十四五”规划支撑专项课题“基于学科核心素养的新高考分数标准参照解释的研究”（课题批准号：NEEA2021043）研究成果之一。

数学学科核心素养是数学课程目标的集中体现，是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现，是在数学学习和应用过程中逐步形成和发展的。包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析。这六个核心素养既具有相对独立性，各自具有鲜明的特征，又组成一个有机整体，具有整合性和综合性的特点[1]4。核心素养的水平主要表现在学生学习数学和运用数学解决问题的过程中，根据问题解决的情况，可以评价学生相应的发展水平[2]。2022年普通高等学校招生统一考试（天津卷）数学试卷（以下简称“试卷”）所考查的核心素养的分布如表1所示。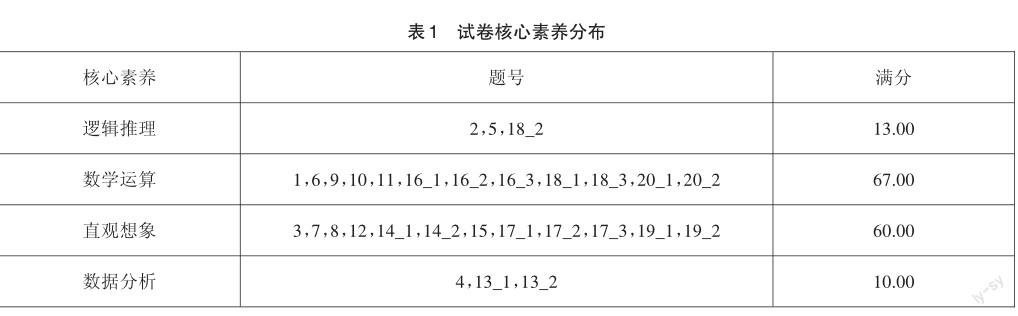

总体看来，试卷突出考查了逻辑推理、直观想象、数学运算、数据分析四大数学核心素养，数学抽象与数学建模两个核心素养虽然没有直接命题考查，但在试卷中也有所渗透。数据显示，对数学运算素养和直观想象素养的考查占有较高的比例。

数学运算是数学活动的基本形式，是解决数学问题的重要途经，是获得问题结果的重要手段，是高中学生应具备的最基本的数学素养。数学运算素养在高考答题过程中的具体表现为：学生在规定时间内理清运算对象的关系，依据数学原理，寻求合理简捷的运算途径，应用运算法则解决问题，正确求解写出规范答案。

以2022年高考考生实测数据为依据，以数学运算的水平划分为标准，评价考生数学运算素养的发展水平，可以指导教师针对提升学生的数学运算素养水平调整教学方案，实施教学策略，开展教学活动，提升教学效果。

一、数学运算素养的概念及水平划分

《普通高中数学课程标准（2017版2020年修订）》（以下简称“《课程标准》”）指出：数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题的素养。主要包括：理解运算对象、掌握运算法则、探究运算思路、选择运算方法、设计运算程序、求得运算结果等。数学运算是演绎推理，是解决数学问题的基本手段也是计算机解决问题的基础。

《课程标准》中将数学学业质量水平分为水平一、水平二、水平三共三个等级，分别对应高中毕业的数学学业水平考试、高考、大学自主招生考试三类不同考试中考生应当达到的要求以及命题依据。高考是基于数学学科核心素养的考试，参考三个维度进行命题。第一个维度是反映数学核心素养的四个方面——情境与问题、知识与技能、思维与表达、交流与反思；第二个维度是反映数学核心素养的四条主线——函数、几何与代数、概率与统计、数学建模活动与数学探究活动；第三个维度是反映各核心素养的三个水平。

对于数学运算素养，《课程标准》从情境与问题、知识与技能、思维与表达、交流与反思四个方面给出了三种不同水平的划分标准。具体内容如表2所示。

由表2可以看出，三个水平在难度上虽然逐级递增，但也体现了整体性和阶段性。其中数学运算素养的四个主要表现，即理解运算对象、掌握运算法则、探究运算思路、求得运算结果，在三个水平的阶段性要求不同。水平一只要求能够在熟悉的数学情境中，根据问题的特征形成合适的运算思路；水平二要求在关联的情境中能够针对运算问题，合理选择运算方法，设计运算程序；水平三则要求在综合的情境中能够针对运算问题，构造运算程序。

二、数学运算素养试题实测数据分析

依据考生答题的典型表现，将考生水平划分为“精通水平”“熟练水平”“基本水平”“基本以下水平”四个等级，依次记为G4、G3、G2、G1组，全体考生记为G5组。临界分数采用安戈夫法来确定，依次为124分、101分、79分，即124-150分为G4组，101-123分为G3组，79-100分为G2组，0-78分为G1组。

试卷考查学生数学运算素养的题目分值为67分，涵盖了集合的运算、对数运算的性质、三角函数的性质、复数的运算、二项式定理、正余弦定理、数列、导数等多个知识点。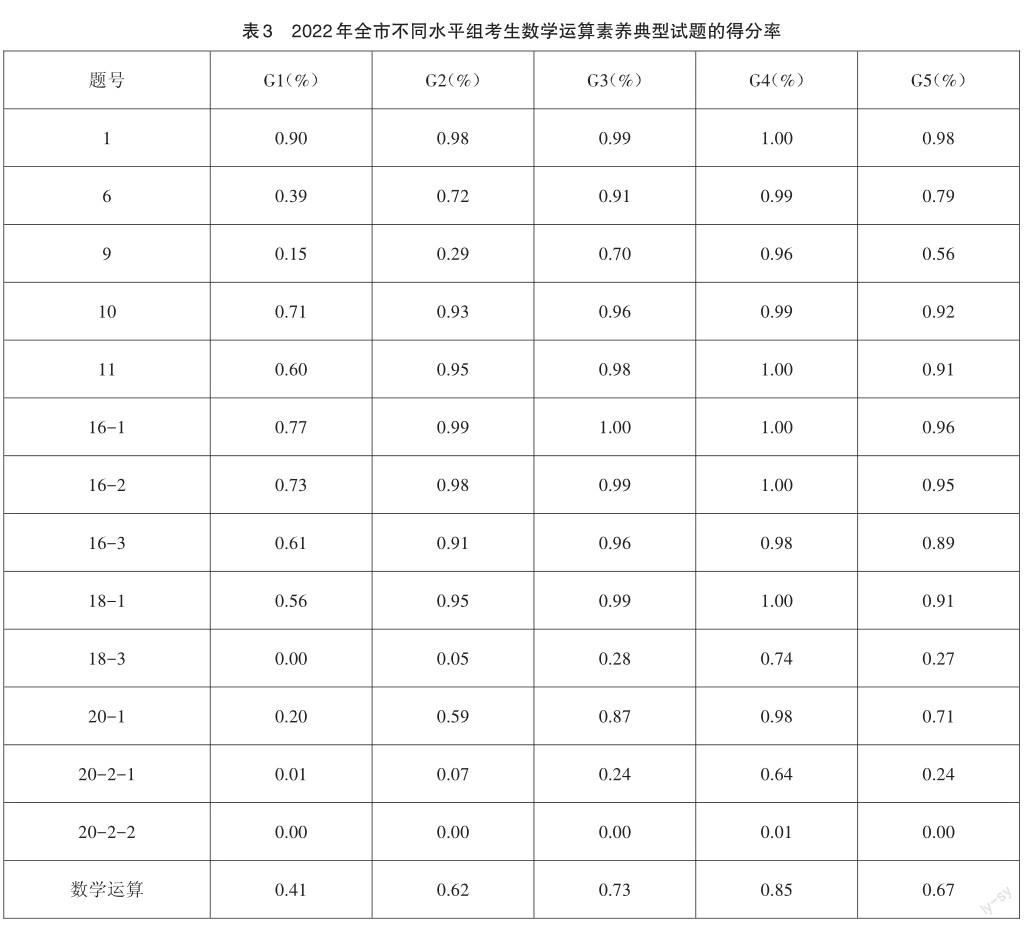

表3反映出2022年不同水平组考生在数学运算素养典型试题的得分率。从数据的具体表现来看，试卷侧重考查数学运算素养的题目分布合理，充分体现了基础知识背景下的素养考核。其中第1题、第10题、第11题、第16题、第18-1题的得分率都比较高，且G2-G4组考生对比没有明显差异，说明绝大部分考生对于基本的、常见的数学运算问题能够达到精通水平，但G1组的表现相对于其他三组存在明顯不足，如第18-1题的得分率仅为0.56。从得分率在0.5-0.8的试题来看，G3和G4组的表现明显优于G2和G1组，而得分率为0.2-0.3的数据则显示，四个水平组存在分化过大的现象，值得关注。

下面以第1题、第18题和第20题为例，对数学运算素养的具体考查情况以及考生的数学运算素养发展水平进行分析。

（一）数学运算水平一试题的考查

例题1：试卷第1题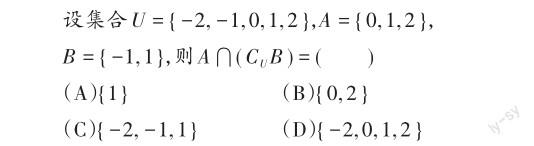

【试题水平划分】本题用列举法表示集合，考查了全集的概念以及补集、交集的基本运算。集合中的元素是离散型的，学生利用观察法或者Venn图，根据集合运算的概念求解即可，是熟悉的数学情境中的运算问题，属于数学运算水平一的要求范畴。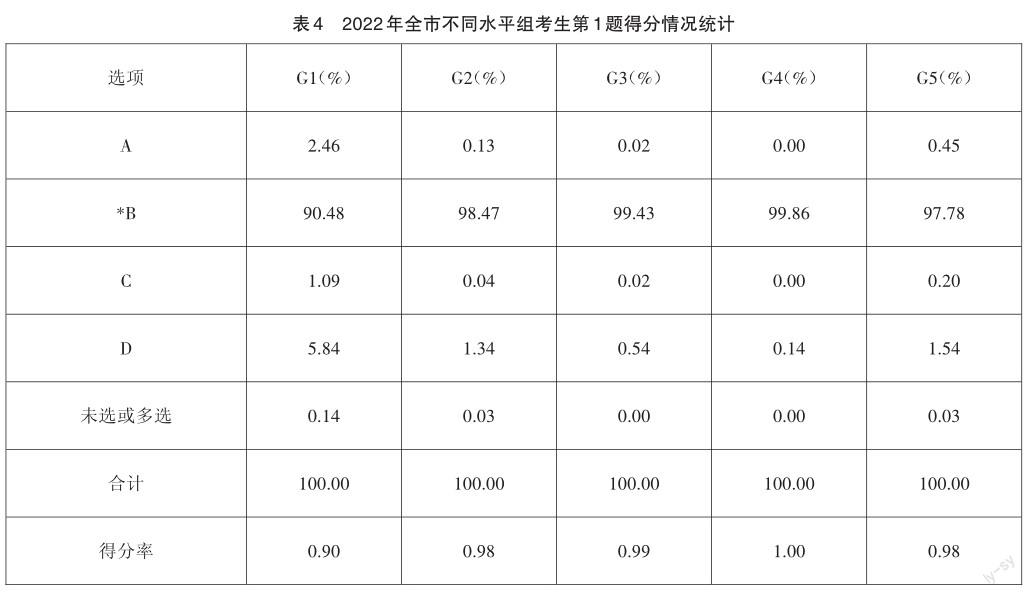

【考生表现】从表4的数据来看，第1题全体考生的得分率为0.98，说明考生對于集合概念的理解以及集合基本运算的掌握还是非常熟练的。由具体数据横向分析，错误选项集中在选项D，显示部分考生对交集符号“？”与并集符号“？”从认知上产生了混淆；纵向比较可以发现，G4-G2组的得分率都高于0.98，但G1组还是有约10%的考生出现错误作答，说明基本水平以下的学生对于集合概念的理解和集合三种基本运算的掌握还有所欠缺。

【教学启示】集合属于高考的重点内容，考查稳定，难度较小，常以选择题的形式呈现，主要是对集合的概念与表示和数集之间的集合基本运算的考查。但集合作为基本的数学语言，能够简洁、准确地表述数学研究对象，这就需要在教学中加强这种数学“语言”的使用，让学生在使用中理解集合的概念、集合间的关系、集合的运算，体会集合这种语言的重要性和必要性。

（二）数学运算水平二试题的考查

【考生表现】第18题的得分率为0.62，本文主要针对考查数学运算素养的第（Ⅰ）问和第（Ⅲ）问的考生表现作具体分析。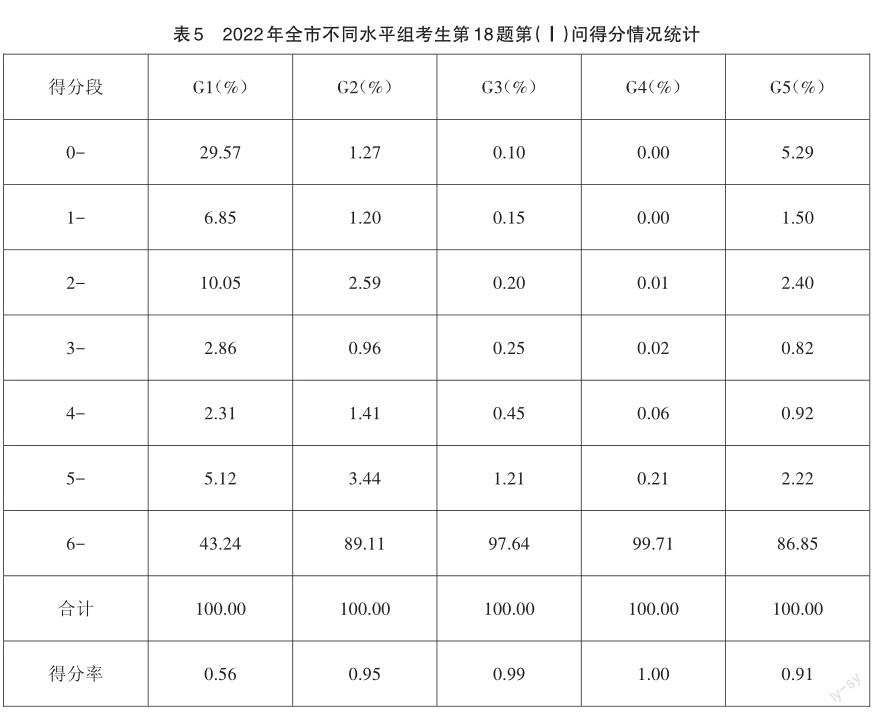

从表5的数据来看，本问全体考生的得分率达到0.91，其中G4、G3和G2组的得分率都在0.95及以上，说明基本水平以上考生的表现还是很突出的。相比而言，G1组表现欠佳，得分率仅为0.56，特别是有接近30%的考生得了0分，这说明基本水平以下考生对于求解数列通项公式这类基本问题仍存在困难，处理方法仍不太明确或者不熟练，在教学中还需要加强训练。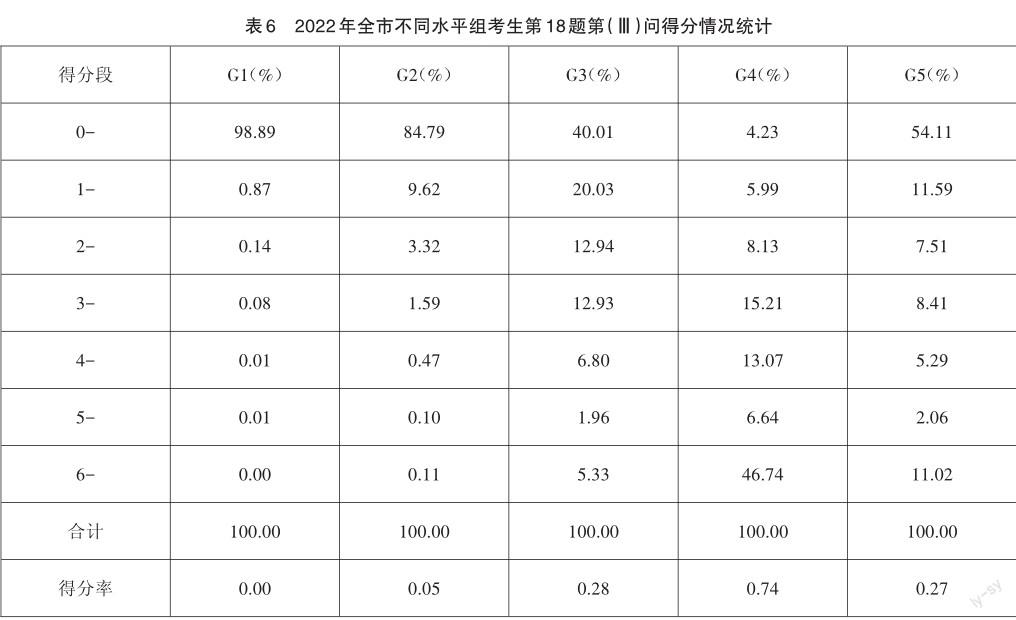

表6数据显示，第18题第（Ⅲ）问的区分度较好，G4-G1组的得分率依次为0.74、0.28、0.05和0.00。通过对比可以发现，G4组考生表现突出，在综合情境中表现出了较高的数学运算素养发展水平。

通过抽样试卷，可以了解不同水平组考生作答本题有以下几种情况：

【教学启示】本题启示教师在数列的教学中要注意以下四个方面：首先，要夯实等差数列和等比数列的基础知识，掌握数列求和中裂项相消、错位相减、分组求和、并项求和等基本方法，加强基本技能的训练；其次，提高学生对抽象数学符号语言的理解和认知，明确数学符号的意义和作用；再次，在不同的问题情境中指导学生积累经验，建构基本模型，使学生能够在分析问题、解决问题的过程中及时获得运算思路，设计运算程序，优化运算方法；最后，要把思维与表达落在实处，不能仅仅“讲”思路“说”方法，要帮助学生运用数学的语言准确规范、逻辑严谨地表达完整的计算或证明过程。

【试题水平划分】本题是一道对数学运算素养进行综合考查的题目，数学运算贯穿于整道题的解题过程。题目综合考查了函数与导数的基础知识，主要围绕导数的几何意义，利用导数研究函数的极值和零点，以及通过不等式放缩构造新函数，应用函数单调性对不等式进行证明来设计问题。第20题共16分，其中第（Ⅰ）问4分，第（Ⅱ）问的两小问的分值均为6分，考查了函数思想、化归与转化思想，考查了学生的逻辑推理和数学运算两大核心素养。前两问达到了数学运算水平二的要求，最后一问属于综合情境下的数学问题，通过每一步运算得到的结果提示进行逻辑推理，得到更加准确明晰的运算思路，达到了数学运算水平三的要求。

【考生表现】本题的全体考生得分率为0.27，属于难题，三问的得分率如表7所示。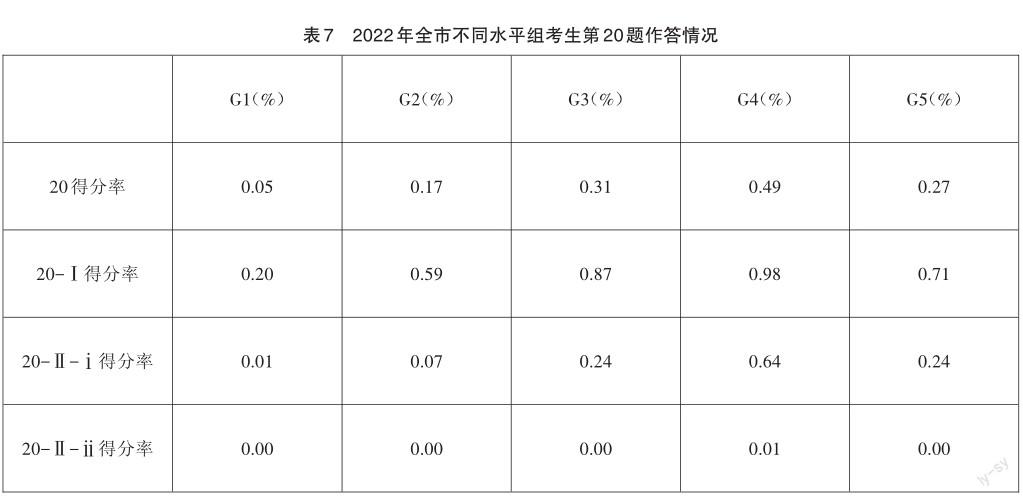

如表8所示，G4组有约36%的考生得到5分，17%的考生得到满分6分，说明对于这部分同学而言，要继续加强培养其逻辑推理与数学运算素养；G1组和G2组分别有93.21%和67.77%的考生得0分，说明考生没有分析题目。

本题最后一问需要考生利用柯西不等式对目标不等式进行放缩，对于一些基本初等函数，如y = ex- （ x + 1），y = x - sinx的性质也需要具备简单的认识，从而合理规划运算路径。由于本问是较复杂的综合情境，又是试卷的最后一题，在有限的时间内学生难以将所证问题与已知结论或方法等建立联系，所以各水平组得分率基本都是0。

【教学启示】高考数学（天津卷）第20题多是考查函数与导数的问题，设计上都比较重视创新性，或问题之间的层层递进（如2020年和2021年天津卷第20题），或问题情境别有新意[如2019年天津卷（理）第20题]，但都是考查学生的逻辑推理和数学运算核心素养，考查学生构造函数的能力和化归与转化的数学思想。本题带来三点启示：第一，要引导学生厘清综合复杂情境中条件和结论之间的关系，培养学生将所证与已知、定理、公理、结论、经验等建立联系的能力。第二，重视通解通法的落实，认真研读教材内容。本题最后一问的放缩利用了柯西不等式，人教版（2019版）数学必修第二册习题6.3的16题对该不等式的内容用向量的方法给出了证明过程，但教学中往往被忽略或一带而过。第三，学生在思维和表达的环节中还不够严谨，说明逻辑推理的训练还不够系统，这也需要引起教学中的关注。

三、教学建议

（一）加强概念教学，明晰运算对象

明晰运算对象是进行数学运算的重要基础。这里的“明晰”包括知道、理解两个层次。这就需要在教学过程中加强概念教学。高中数学有更多更抽象的数学概念，有些概念还容易使学生产生混淆。如例题1中的交集和并集，又如充要条件、充分不必要条件、必要不充分条件等。教师在授课时，对概念要讲解清楚，辨析到位。教学中可通过举反例、类比与对比等方法加强学生对概念的理解。

在高中的数学运算中，运算对象不仅仅是数与式，还包括函数、向量、数列、复数等。因此在运算之前，首先要看清、看准运算对象。其次，要深层次理解运算对象，即了解运算对象的背景，理解运算对象的本质、成立条件、几何意义、关联概念及相关数学思想方法等。如“f （ x ）是奇函数”，多数学生想到的只是f （ -x ） = -f （ x ），但还应联想到其定义域关于原点对称、图象关于原点对称等。因此，在教学中教师应该将概念教学安排在首位，让学生以理解概念为基础，指导学生在运算过程中加深对运算对象的再理解、再认识，明晰运算对象的“所指”和“能指”。只有对运算对象及其特征了然于心，明确运算对象概念的内涵和外延，才能在面对运算对象时找准切入点与落脚点，使数学运算自然顺畅进行。

（二）夯实基础知识，掌握运算法则

掌握运算法则是开展数学运算活动的重要保证。高中数学中，不同的运算有不同的运算法则或运算规律，例如集合的运算、函数运算、三角运算等。运算对象不同，则运算法则也存在明显的差异。

因此，教学中需要注意以下三点：第一，围绕运算对象指导学生总结相关的运算法则，借助图表培养学生勤梳理、勤思考的习惯；第二，结合教学内容设计相关问题情境，为学生提供运用运算法则解决问题的机会，在实践中提高学生应用法则的熟练程度；第三，注重基础知识的讲解，从算理上让学生理解数学运算法则，使学生不仅“知其然，知其所以然”，更能“何由以知其所以然”。

（三）尝试一题多解，选择运算路径

运算路径是数学运算的核心所在，教会学生选择运算路径是解决数学问题的关键。2021与2022年高考数学（天津卷）平面解析几何解答题都聚焦于直线与椭圆相切的位置关系。从作答情况来看，很多考生在模式化的训练中，陷入了思维固化的困境。面对试题，遇到了“算什么”“怎么算”“算不对”等诸多问题。

选择合适运算路径的前提是要理解题意，明确运算对象，知晓运算法则，要能进行概念、定理、性质之间的相互转化。要在从“问题”开始，到“问题”结束的过程中，指导学生探究解题思路，选择运算路径。教学实践中可以引导学生提出以下问题：已知条件是什么？得到结论需要什么条件？二者之间的关系是什么？此题与以前做过的哪些题类似？解决这类问题的途径有哪些？在这个过程中，切忌以教师的认知结构去代替学生的认知，以教师的解题习惯等同于学生的习惯。

另外，一题多解是优化运算路径的行之有效的方法。如前文所示18题第（Ⅲ）问数列求和的不同方法。教学中要多创设适宜学生思维发展的问题情境，激发学生的创新思维，深化学生对问题的理解，优化运算思路，提升学生解决问题的能力，使学生在探究不同运算思路的过程中积累数学活动经验，为设计合理简捷的运算路径做出铺垫。

（四）规范解题步骤，求得运算结果

求得运算结果是实施数学运算的最后一步。对于学生数学运算素养的培养不仅要关注知识、技能、思维，还要关注表达能力。通过对试卷的抽样分析可以发现，学生对综合情境下主观题的表达普遍表现较弱，解题步骤与过程的规范性也有所欠缺。因此，教学中除了关注学生在数学运算演绎推理中表现的深刻性、新颖性等思维品质，也要关注学生在运算过程和结果表述中的严谨性与准确性。

教学中可以发现，多数学生对运算问题不够重视。对于简单的问题表现得眼高手低，认为只要想想思路就解决了问题，不能静下心来一算到底；对于复杂的问题又表现得缺乏自信、畏首畏尾，不肯花时间去探究，考试时遇到类似问题就直接选择放弃。因此，在教学过程中，教师不能只给出解题思路，也不能总是由教师示范表达，应当突出运算作用，给予学生足够的运算机会及运算指导。要让学生主动参与，并独立完成规范表达。要利用课堂教学强化学生的運算能力，提高其严谨的表达水平。同时，要指导学生养成对运算结果进行分析与反思的习惯。通过运算结果对数学问题进行检查和验算，这不仅是数学运算的必要步骤，也是对知识再巩固的过程。

数学运算素养在高考中是重点考查的数学学科素养，且多以数学核心素养水平划分中“水平二”的要求为目标。高三学生大多已具备较好的运算基础、认知水平和数学素养水平，建议教师在教学中多创设关联情境和综合情境问题，关注明晰运算对象、掌握运算法则、选择运算路径、求得运算结果四个环节，让学生在数学运算的过程中养成敢质疑、善思考、规范严谨的科学态度，从而有计划、有目的地落实和提升学生的数学运算素养水平。

参考文献：

[1]中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）[M].北京：人民教育出版社，2020.

[2]谭毅，沈婕，刘勇，等.直观想象素养的水平划分与评价——以2021年高考数学（天津卷）为例[J].考试研究，2022，（3）：1-10.

Level Division and Assessment of Mathematics Operation Literacy

Li Ying1Shen Jie2Liu Yong3Wang Hongliang4Tan Yi5

1 Tianjin Experimental High School，Tianjin，300074 2 Tianjin Academy of Educational Science，Tianjin，300191 3 Tianjin Binhai Hangu No. 1 Middle School，Tianjin，300480 4 Tianjin Yaohua High School，Tianjin，300040 5 Tianjin Nankai High School，Tianjin，300100

Abstract：Based on the actual data of the Mathematics Test of Tianjin College Entrance Examination in 2022，this paper analyzes the development of studentscore mathematics literacy with reference to the level division of High School Mathematics Curriculum Standards. In view of the problems students are faced with in Mathematical Operation Literacy，the paper puts forward some suggestions about the math teaching in senior high from four aspects：explicating mathematical operands，mastering the algorithm，selecting mathematical operation path，and getting the operation results.

Key words：Mathematics Core Literacy，Mathematics Operation Literacy，Level Division，Assessment

（責任编辑：吴茳、许志勇、白云）