“平行四边形和梯形”的整理与复习

文|章瀚文 杨灵巧

一、多层次体会图形间的转换关系

1.理一理。

同一平面内两条直线会有怎样的位置关系呢？

2.想一想。

展开想象：屏幕上有一组平行线，如果再来一组平行线，可能会出现一个怎样的四边形；如果再来一组相交的直线呢？分别举例说一说。

3.选一选（把符合条件的序号填在括号里）。

A.对边相等

B.两组对边互相平行

C.邻边相等

D.只有一组对边互相平行

E.邻边互相垂直

F.上底和下底相等

4.指出：正方形是特殊的长方形，长方形是特殊的平行四边形，直角梯形和等腰梯形是特殊的梯形。

二、多维度辨析平行四边形与梯形的联系

1.辨一辨。

学生根据图1 辨析：这两个图形是平行四边形吗？思考：怎么改才能变成平行四边形？

图1

2.学生独立完成，小组交流。

3.全班反馈，归纳修改方法。

得出结论：平行四边形的一组对边平行且相等，只要上底和下底一样长就可以得到平行四边形，结合高就是两条平行线之间的距离，进而复习同底等高的平行四边形。

三、多模块探索规律，建构数学模型

1.出示图2，展开想象，寻找第4 个点，使它们围成平行四边形。

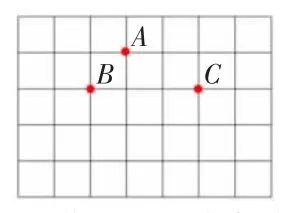
图2

2.展示作品，反馈交流。

（1）以BC 为底，第4 个点只要在过A 点BC 的平行线上，并且与A 点的距离是3 格的位置就能组成平行四边形，因此距离A 点右边3 格能找到D1，距离A 点左边3 格能找到点D2。

（2）方法延伸，除了以BC 为底，还能以哪条边为底？

以AB 为底，只要在过C 点作AB的平行线上，距离C 点的距离与线段AB 相等，可以找到D3、D4。

以AC 为底，只要在过B 点作AC的平行线上，距离B 点的距离与线段AC 相等，可以找到D5、D6。

（3）D1、D2、D3、D4、D5、D6两两重合，因此符合要求的D 点只有3 个。

3.交流方法，建构模型。

只要寻找已知直线的平行线，在平行线上去寻找第4 个点。

用一用：还是这三个点，通过寻找第4 个点，使得它们组成梯形，渗透有序思考的数学思想方法，提升多角度分析解决问题的能力，在寻求规律中建构数学模型，发展空间观念。