例谈主元法在多变量函数问题中的运用

福建省南安第一中学 (362300) 卢 阳

复杂的函数中一般含有常量、变量、参数等多个量.解题时常选某个处于突出的、主导地位的量作为研究对象,以此为主线来分析、解决问题,我们称之为主元法.在某些情况下,按照解题经验或思维定势来确定主元,可能会导致问题复杂化.此时,若能改变视角,重新选择主元,往往会收到柳暗花明的效果.另外,若题目中几个变量处于平等对称地位,不知从何下手,便可指定其中一个量为主元,进而继续研究.[1]本文举例说明.

一.变换主元,另眼看题

分析：本题有三个变量a,x,k,通常情况下把x当成主元,但是此时函数很复杂,不易处理.不妨转变视角,以a为主元,函数变为易于研究的二次函数.

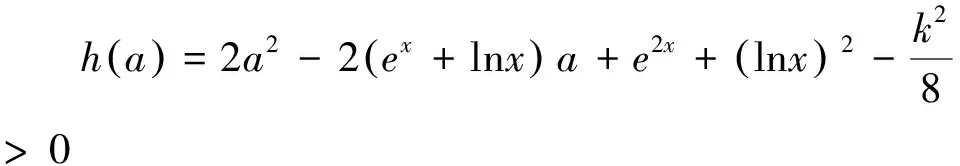
评析：本题有三个变量,按照思维定式,选x为主元,函数不易研究.如果转换角度,以a为主元,函数研究起来自然顺畅.主元分析的掌握程度能够体现学生对函数概念的理解,以及用辩证的眼光去看待问题和解决问题的思维能力,解题过程中考查学生的逻辑推理与数学运算等核心素养.[2]

二.委以重任,指定主元

分析：本题有两个变量x,y,观察所求的代数式形式,指定y为主元进行解题更为方便.

分析:从函数角度来看,此题含有三个变量,地位平等,若不选择主元则不知如何研究,不妨选x1为主元,对其委以重任.

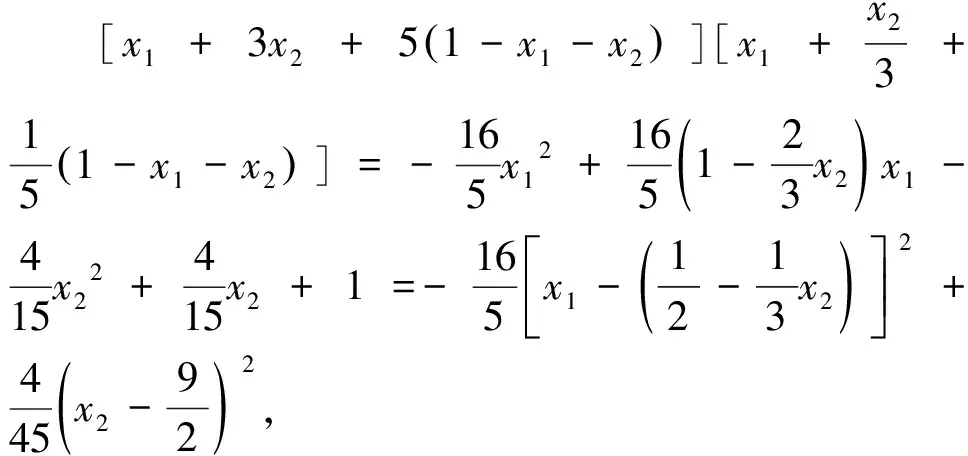
评析：例2、例3中的变量地位相当,解题时不知那个变量是着力点,不妨选择其中一个变量指定其为主元,剩下变量为常量,这样便抓住了主要矛盾,减少学生对难题的恐惧.解题时,主元法发挥了消元的作用,可谓精彩.

三、各元牵制,使用不当

分析：此题是双变量问题,可能会选择x1,x2中的一个为主元进行解题.但与前几例不同,题中两元并不独立.

又因为(x1-1)lnx1-a(x1+1)=0,

评析：此题中两元存在x1x2=1的关系,因此各元之间不满足“无牵无挂”的前提条件,而有关系进行制约,因此每一步的取等条件可能不符合两元的等量关系,故不可使用主元法.应该利用两变量的等量关系进行消元,进一步转化为单变量函数问题.

由上述实例可见,常量与变量是相对的,两者在一定条件下可以互相转换.涉及多变量函数问题时,要敢于打破常规,从多个变量中选择合适的主元着重使力,便可以从模糊纷乱的思绪中找到坚定的方向,拨开云雾见青天.主元法视野广阔,不仅能够很好地考查学生的创新意识和逻辑思维能力,也能培养学生在复杂开放的情境下解决问题的勇气与能力,值得读者认真品味.[3]当然,任何方法都不是万能的,使用时需要考虑主元的范围是否已知以及各元之间是否存在牵制关系.