论常量函数的充分必要条件

孙 兰 敏

(衡水学院 数学与计算机科学学院，河北 衡水 053000)

论常量函数的充分必要条件

孙 兰 敏

(衡水学院 数学与计算机科学学院，河北 衡水 053000)

常量函数是最简单的函数，判定满足某些条件的函数是否为常量函数并不简单.由拉格朗日中值定理容易得出：“在区间I上f(x)为常量函数的充分必要条件是对任意的x∈I都有f′(x)=0”.在此基础上进一步给出并证明了函数为常量函数的另外几个充分必要条件，在理论上为证明“满足某些条件的函数是常量函数”提供了切实可行的证明方法.

常量函数；连续；极限

由拉格朗日中值定理容易得出下面结论：

定理[1]设f(x)在区间I上有定义，则f(x)为常量函数的充分必要条件是对任意的x∈I都有f′(x)=0.

该定理是研究函数是否为常量函数的重要依据，但证明函数为常量函数的方法远远超过于此，下面给出并证明函数为常量函数的几个充分条件，易见这些条件也是必要的.

命题1设f(x)在(0,+∞)满足f(x)=f(2x)，并且=A，则在(0,+∞)上f(x)为常量函数，并且f(x)=A.

证明假设存在x0∈ (0, +∞)使f(x0)≠A，由已知条件f(x)=f(2x)得：对任意的正整数n有B=f(x0)=f(2x0)=…=f(2nx0)≠A，另一方面由已知条件=A得：对ε=A−B＞0，存在正数X，使得当x＞X时有：f(x) −A＜ε，取n足够大使 2nx＞X则有，即

所以，对任意的x∈(0,+∞)有f(x)=A.

命题2设f(x)在R上有定义，在x=0,1两点连续，若对任意x∈R有f(x)=f(x2)成立，则f(x)在R上为常量函数.

证明

1) 证明对任意x∈[−1,1]有f(x)=f(0).

事实上：对任意x∈(−1,1)并且x≠0，由所给条件得：对任意的正整数n有：f(x)=f(x2)=f(x4)=…f(x2n)，因为：f(x)在x=0连续，所以：

由f(x)在x=1连续知：f(1 )=xli→m1−f(x) =f(0).

由以上可知：对任意x∈[−1,1] 有f(x) =f(0).

2) 证明对任意x∈(1,+∞)有f(x)=f(0).

事实上：对x∈(1,+∞)，反向利用已知条件得：

对任意的正整数n有：

3) 证明对任意x∈(− ∞,−1)有f(x)=f(0).

事实上，若x∈(− ∞,−1)，则x2∈ (1,+∞)，从而f(x)=f(x2)=f(0).

综上所述，对任意x∈R有f(x)=f(0).故f(x)在R上为常量函数.

命题3设f(x)在R上有定义，若对任意的a,b∈R恒有：成立.(其中：α＞1，M＞0，均为常数)，则在R上f(x)是常量函数.

证明设α=1+β(β＞0)，任取x0∈R，x∈R，则由已知条件得：

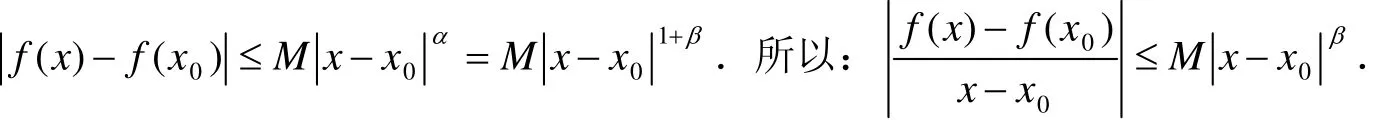
令x→x0则得：f′(x0)=0，由x0的任意性知对任意的x∈R均有f′(x)=0，所以f(x)是常量函数.

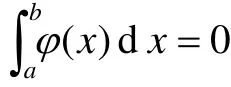
因而有：

显然有：

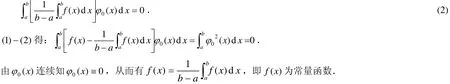
[1] 刘玉琏,傅沛仁.数学分析讲义:上册[M].北京:高等教育出版社, 1992:207.

The Judgment of Constant Function

SUN Lan-min
(College of Mathematics and Computer Science, Hengshui University, Hengshui, Hebei 053000, China)

Constant function is the simplest function, but its judgment is not simple. It is clear to see from Lagrange theorem“The enough and essential condition off(x)being constant function isf/(x)≡0”. Several enough and essential conditions off(x) being constant function are given to prove it. It also supply practical ways to prove that “function meeting certain requirements is constant function”.

a constant function; continuation; limit

O174

A

1673-2065(2011)04-0006-02

2011-02-20

孙兰敏(1963-),女,河北深州人,衡水学院数学与计算机科学学院教授.

(责任编校：李建明英文校对：李玉玲)