学思探微，归纳剖析——备考不等式及其解法

■四川省绵阳实验高级中学 黄 芹

在近几年的高考解答题中,关于不等式的考查主要包括解一元二次不等式、指对数不等式、三角不等式等。在高考选填题中,还常常涉及利用函数图像解不等式、利用函数单调性解不等式等。本文旨在归纳不等式及其解法的题目类型,挖掘做题方法和技巧,希望对同学们的复习备考能有所帮助。

类型一、利用函数图像解不等式

抓住函数图像特征(定义域、值域、对称性、单调性、周期性和特殊点等),结合函数图像和选项确定答案。

例 1(2023 年商丘模拟)已知定义在R上的奇函数f(x)在[0,+∞)上的图像如图1 所示,则不等式x2f(x)＞2f(x)的解集为( )。

图1

解析：根据奇函数图像的特征,作出f(x)在(-∞,0)上的图像,如图2所示。

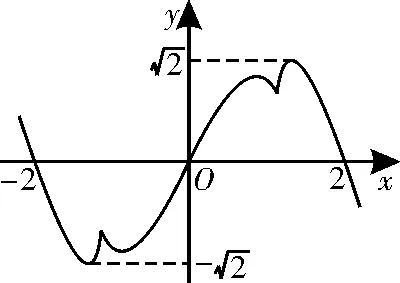
图2

由x2f(x)＞2f(x),得(x2-2)f(x)＞0,则结合f(x)的图像解得x＜-2或或。

例 2(2023 年贵阳模拟)设函数f(x)的定义域为R,满足f(x+1)=2f(x),且当x∈(0,1] 时,f(x)=x(x-1)。若对任意的x∈(-∞,m],都有f(x)≥-成立,则m的取值范围为( )。

解析：已知当x∈(0,1]时,f(x)=x(x-1),f(x+1)=2f(x)。

所以当x∈(1,2]时,f(x)=2f(x-1),即f(x)向右平移1个单位长度,纵坐标变为原来的2倍。

当x∈(2,3]时,f(x)=4f(x-2)=4(x-2)(x-3),如图3所示。

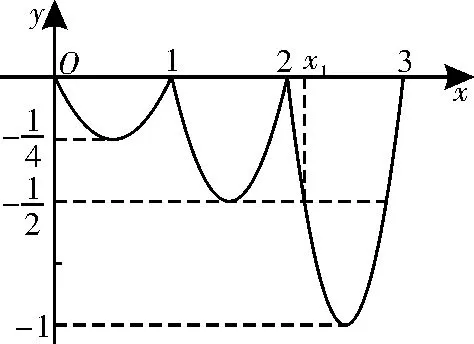
图3

令4(x-2)(x-3)=,解得x1=。

所以要使对任意的x∈(-∞,m],都有成立,则。

所以m的取值范围为。故选B。

点睛:对f(x+1)=2f(x)的理解是画出函数图像的关键。解不等式转化为找y=上方的图像所对应的x的取值范围。

类型二、由表达式直接运算解不等式

解一元二次不等式、指数不等式、对数不等式、含绝对值的不等式是直接求解不等式的常见题型。解指对数不等式的关键是熟练掌握指对数运算法则及指对数函数的图像特征。解含绝对值不等式的关键是能否利用零点分段法去掉绝对值。

例3(2023 年重庆质检)已知函数则f(x)＜f(x+1)的解集为_____。

解析：当x≤0 时,x+1≤1,f(x)＜f(x+1)等价于x2-1＜(x+1)2-1,解得;

当0＜x≤1时,x+1＞1,此时f(x)=x2-1≤0,f(x+1)=log2(x+1)＞0,所以恒有f(x)＜f(x+1);

当x＞1时,x+1＞2,f(x)＜f(x+1)等价于log2x＜log2(x+1),此时也恒成立。

综上可得,不等式f(x)＜f(x+1)的解集为。

点睛:本题的解答可归结为解一元二次不等式和对数不等式。解对数不等式的关键是利用对数函数的单调性。

例4(2023 年南昌模拟)已知函数f(x)=log3(9x+1)+kx是偶函数。

(1)求k;

(2)解不等式f(x)≥log3(7·3x-1)。

解析：(1)因为f(x)是偶函数,所以f(-x)=f(x),即log3(9-x+1)-kx=log3(9x+1)+kx对任意的x∈R 恒成立,所以2kx=log3(9-x+1)-log3(9x+1)=,所以k=-1。

(2)由(1)得f(x)=log3(9x+1)-x=(3x+3-x),则不等式f(x)≥log3(7·3x-1)等价于3x+3-x≥7·3x-1＞0。

由7·3x-1＞0,解得x＞-log37;

由3x+3-x≥7·3x-1,得6·(3x)2-3x-1≤0,得,即x≤-log32。

综上可得,所求不等式的解集为(-log37,-log32]。

点睛:第(2)问解对数不等式,转化为解指数不等式和一元二次不等式。解指数不等式的关键是利用指数函数的单调性。

例5(2023年上海高三专题练习)已知a,b,c∈R,若关于x的不等式0≤x+的解集为[x1,x2]∪{x3}(x3＞x2＞x1＞0),则( )。

A.不存在有序数组(a,b,c),使得x2-x1=1

B.存在唯一有序数组(a,b,c),使得x2-x1=1

C.有且只有两组有序数组(a,b,c),使得x2-x1=1

D.存在无穷多组有序数组(a,b,c),使得x2-x1=1

解析：由题意知不等式0≤x2+bx+a≤c-x,即的解集是[x1,x2]∪{x3}(x3＞x2＞x1＞0),则不等式x2+bx+a≥0的解集是{x|x≤x2或x≥x3},不等式x2+bx+a≤c-x的解集是{x|x1≤x≤x3}。

①-②得x2-x1=1,所以存在无穷多组有序数组(a,b,c),使得x2-x1=1。故选D。

点睛:本题解答的关键是转化求一元二次不等式的解集,从而结合一元二次方程根与系数的关系得出结论。

类型三、利用函数的单调性解不等式

例6(2023 年扬中检测)已知函数f(x)在定义域[2-a,3]上是偶函数,在[0,3]上单调递减,并且f(-m2+2m-2),则m的取值范围是_____。

解析：因为函数f(x)在定义域[2-a,3]上是偶函数,所以2-a+3=0,解得a=5,所以f(-m2-1)＞f(-m2+2m-2)。

因为f(-x)=f(x)=f(|x|),所以f(|-m2-1|)＞f(|-m2+2m-2|)。

又因为f(x)在[0,3]上单调递减,所以解得。故m的取值范围是。

点睛:本题是利用抽象函数的奇偶性和单调性解不等式,特别是偶函数的性质。

点睛:观察不等式的结构特点,构造相应的函数,分析函数的单调性,从而应用单调性解不等式。

类型四、讨论函数的单调性

已知函数的解析式,讨论函数的单调性,本质上是解不等式f'(x)＞0,f'(x)＜0。含参数的不等式需要对参数进行分类讨论,讨论的依据常常是判断对应方程是否有实根及比较对应方程的根的大小,考查函数、方程、不等式之间的相互转化,是综合性题目。

例8(2023 年合肥质检)已知函数,试讨论函数f(x)的单调性。

点睛:解含参一元二次不等式时,应先判断对应一元二次方程是否有实根,再讨论一元二次方程的根的大小。

例9(2023年山西联考模拟预测)设函数f(x)=(x+1)ex+m(x+2)2,m∈R,讨论f(x)的单调性。

解析：依题意得f'(x)=(x+2)ex+2m(x+2)=(x+2)(ex+2m)。

①若m≥0,则当f'(x)＜0 时,得x＜-2;当f'(x)＞0时,得x＞-2。所以f(x)在(-∞,-2)上单调递减,在(-2,+∞)上单调递增。

点睛:通过判断方程(x+2)(ex+2m)=0的根的个数及比较方程根的大小来讨论函数f(x)的单调性。

备考不等式及其解法,打好基础是关键,基础知识包括熟练掌握基本初等函数的图像和性质,函数与方程、不等式的关联和转化,灵活运用函数图像、函数性质解不等式,典型题目掌握通性通法才能做到融会贯通,灵活运用。