立体几何中空间向量运算的易错题分析
■江苏省南京市板桥中学 纪明亮
立体几何是高中数学中的重要知识点,将立体几何与代数融合引进了空间向量。空间向量强调几何直观和代数运算,能培养同学们的直观想象和数学运算等核心素养。空间向量是处理立体几何问题的重要工具,但运用空间向量解题时还存在误区。下面笔者分析几类空间向量运算中的易错题,相信这对同学们更具有实战价值,具体过程如下。
易错点一、坐标系建立错误
例1(宁波市2023年高三模拟试题)如图1,在四棱锥P-ABC中,平面PAB⊥平面ABC,平面PAC⊥平面ABC,PA=AC=2AB=2,,求锐二面角P-BC-A的余弦值。

图1
错因分析:建立空间直角坐标系需找到过同一点的三条直线,且两两垂直。该情况等价与两条相交直线互相垂直,第三条直线过垂足且与这两条直线所在平面垂直。上述解法由平面PAB⊥平面ABC,平面PAC⊥平面ABC,不能直接得到PA⊥AB,PA⊥AC。
易错点二、错把向量坐标当作点坐标
例2(扬州市2023 届高三考前调研测试题)如图3所示,平行六面体ABCDA1B1C1D1的体积为6,截面ACC1A1的面积为6。若AB=AD=2,,AA1,点B到平面ACC1A1的距离为1,求直线BD1与平面CC1D1D所成角的正弦值。
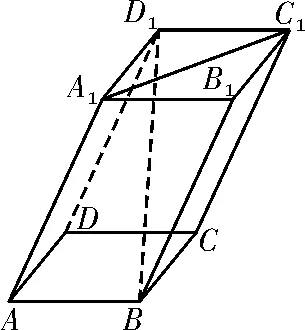
图3
错因分析:上述解法在由的坐标当作点D1的坐标,导致错误。在求某向量的坐标时,若该向量一端点的坐标不易求出,则可借助相等向量,这是一种间接求向量坐标的重要方法。
正解:前面同错解。
易错点三、错把线段比值当作线段长度
正解:前面同错解。
易错点四、求点面距离时夹角判断错误
例4如图7,在多面体ABCDEF中,四边形ABCD与四边形ABEF均为直角梯形,平 面ABCD⊥ 平 面ABEF,AD∥BC,AF∥BE,AB⊥AD,AB⊥AF,AB=AD=2BC=2BE=2,且AF>1。若点F到平面CDE的距离为,求平面CDE与平面BDF所成锐二面角的余弦值。

图7
错解:因为平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,AD⊂平面ABCD,AD⊥AB,所以AD⊥平面ABEF。
错因分析:根据法向量求点到直线的距离时,错把向量模乘以该向量与法向量夹角的正弦。若平面α的法向量为n,O∈α,A∉α,则点A到平面α的距离为。
正解:前面同错解。
直观想象和数学运算是同学们必备的数学素养,立体几何空间向量很好地将二者结合,使之成为一个有机的整体,因此,空间向量运算是同学们必须要掌握的。分析错误有助于厘清运算思路,悟透运算道理,理解知识内涵。以上是笔者对立体几何中空间向量运算的易错题所做的分析,希望对同学们的复习备考能有所帮助。

