探析立体几何中的轨迹问题

■四川省绵阳实验高级中学 罗 娟

在高中数学的学习过程中,要注重数学的不同分支和不同内容之间的联系,高考大纲也提出了数学整体性和综合性的要求,于是立体几何与解析几何作为几何的两个分支,两者“联姻”而成的题型逐渐成为高考与各省市模拟中的“热点”。这类题型立意新,知识交叉渗透,有些同学常感到无从下手,本文将通过所求轨迹的种种类型来介绍如何找到这类问题的突破口,从而顺利解决问题。

一、轨迹为点型

例1已知平面α∥平面β,直线l⊂α,点P∈l,平面α,β间的距离为4,则在平面β内到点P的距离为5且到直线l的距离为9 2的点的轨迹是( )。

A.一个圆 B.两条平行直线

C.四个点 D.两个点

解析：如图1,设点P在平面β内的射影是O,则OP是平面α,β的公垂线,OP=4。在平面β内到点P的距离等于5的点到O的距离等于3,可知所求点的轨迹是平面β内以O为圆心,3为半径的圆。又在平面β内到直线l的距离等于的点的集合是两条平行直线m、n,它们到点O的距离为,所以直线m、n与这个圆均相交,共有四个交点,因此所求点的轨迹是四个点。故选C。

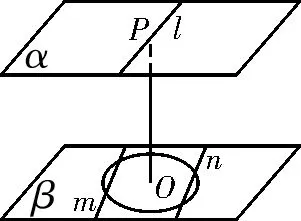
图1

点评:把空间的距离问题转化为平面问题来解决。

二、轨迹为直线型

例2平面α的斜线AB交α于点B,过定点A的动直线l与AB垂直,且交α于点C,则动点C的轨迹是( )。

A.一条直线 B.一个圆

C.一个椭圆 D.双曲线的一支

解析：设l与l1是过点A且与AB垂直的任意的两条直线,则这两条直线确定了一个平面β,由题意可得AB⊥β,由于过一点有且只有一个平面与已知直线垂直,因此平面β是唯一的,所以动点C都在平面α与β的交线上。故选A。

点评:熟练掌握立体几何中的公理、定理,对于解决问题有很大的帮助。

三、轨迹为曲线型

1.轨迹为椭圆

例3在三棱柱ABC-A1B1C1中,二面角A-CC1-B的大小为30°,动点M在平面ACC1A1上运动,且M到平面BCC1B1的距离d=MA,则点M的轨迹为( )。

A.直线 B.抛物线

C.双曲线 D.椭圆

解析：如图2,过点M作MN垂直平面BCC1B1于点N,作MD垂直CC1于点D,连接MD,由三垂线定理得DN⊥CC1,所以∠MDN=30°,则,由圆锥曲线的第二定义可知点M的轨迹为椭圆。故选D。

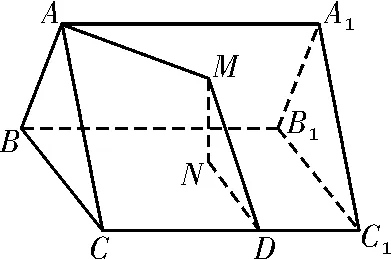
图2

点评:利用二面角为定值这一特点转化为椭圆的定义。

2.轨迹为抛物线

例4如图3,在正方体ABCDA1B1C1D1中,P是侧面BB1C1C内一动点,若P到直线BC与直线C1D1的距离相等,则动点P的轨迹所在的曲线是( )。

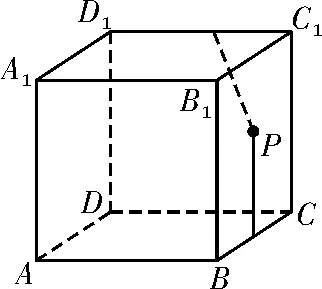
图3

A.直线 B.圆

C.双曲线 D.抛物线

解析：由C1D1⊥平面BB1C1C,得PC1⊥C1D1,所以PC1就是点P到直线C1D1的距离,故条件转化为点P到BC的距离等于点P到点C1的距离。根据抛物线的定义知点P的轨迹所在的曲线是抛物线。故选D。

点评:本题的解答巧妙利用了题中某些定值定量条件,转化为定义法来判定动点轨迹。这其实也是解析几何中求轨迹问题常用的方法之一。

3.轨迹为双曲线

例5已知直线e⊂α,点P∉α,过点P引与直线e成45°角的直线交平面α于点Q,则点Q的轨迹是( )。

A.两个点 B.双曲线

C.椭圆 D.抛物线

解析：如图4,过点P作PO⊥α于点O,以过点O与直线e平行的直线为y轴,以OP为z轴建立空间直角坐标系,过点Q作OA⊥x轴于点A。设Q(x,y,0),则A(x,0,0),由于P点固定,不妨设P(0,0,h),由题意知OA=PA,所以y2=x2+h2。故选B。

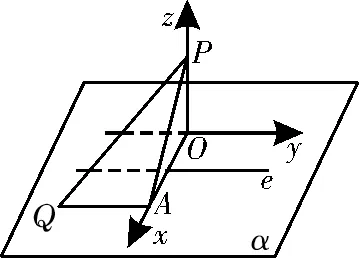
图4

点评:建立空间直角坐标系把立体几何与解析几何直接联系起来。

四、轨迹为空间图形

例6如图5所示,已知在每条棱长都为3 的直平行六面体ABCD-A1B1C1D1中,∠BAD=60°,长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN的中点P的轨迹与直平行六面体的面所围成的几何体的体积为( )。

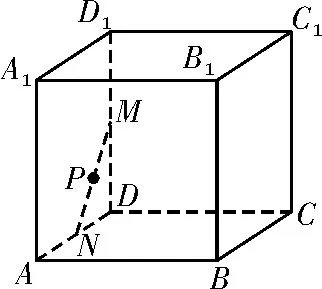
图5

解析：由题意知,当点M或N与点D重合时,DP=1;当不重合时,M,N,D三点构成直角三角形,DP为斜边上的中线,DP=1。所以点P的轨迹是以D为球心,半径为1的球在直平行六面体内的部分。由题意知∠ADC=120°,所以。故选B。

点评:利用MN为定长这一特点,巧妙转化为球的定义进行求解。

通过以上几例,不难发现,解决立体几何中的轨迹问题的关键在于把不同平面上的条件转化到同一平面中去,然后用解析几何方法去求轨迹。