依托立体几何,传播数学文化

■江苏省梁丰高级中学 黄耀平

立体几何作为高中数学中的一大主干知识,也是中国古代数学的一个重要载体与应用场景。从中国古代数学中挖掘立体几何的相关素材,综合考查立体几何的有关知识,既符合考生的认知水平,又可以引导考生关注中华优秀传统文化,成为新高考数学命题中比较热点的应用之一。

一、空间几何体的表面积或体积问题

例1《九章算术》是中国古代的数学专著,书中记载有如下一个问题:“今有圆亭,下周三丈,上周两丈,高一丈,问积几何。”意思为:“今有一圆台体建筑物,下周长为3丈,上周长为2 丈,高为1 丈,问它的体积为多少。”则该建筑物的体积(单位:立方丈)为( )。

解析：依题知下周长为3丈,则下底面圆的半径。又上周长为2丈,则上底面圆的半径)。所以该建筑物的体积故选D。

点评:本题以优美的圆台几何体为背景,通过测量上、下底面的周长及高来确定对应的体积问题。圆台是中国古代建筑中比较常用的一个几何场景,应用非常广泛。

二、立体几何中的空间角问题

例2在中国古代数学专著《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”。已知在“堑堵”ABC-A1B1C1中,AB⊥AC动点M在“堑堵”的侧面BCC1B1上运动,且AM=2,则∠MAB的最大值为( )。

解析：在直棱柱ABC-A1B1C1中,作AO⊥BC于点O,所以AO⊥平面BCC1,所以△AOM为直角三角形。又因为AB⊥AC,,所以O为BC的中点,且△ABC是等腰直角三角形,所以AO=。而动点M在侧面BCC1B1上运动,且AM=2,则M在以A为球心,2为半径的球面上,结合AO⊥ 平面BCC1,则M在以O为圆心,为半径的圆上,如图1所示,直径为PQ,所以,所以,则当BM取最大值BP时∠BAM最大,此时BP,所以cos ∠BAP。故选B。

图1

点评:借助特殊空间几何体“堑堵”为问题场景,通过特殊空间图形中的对应线段长度与位置关系等来设置,结合动点轨迹的变化来确定对应空间角的最值问题。这里巧妙将中国古代的优秀数学文化与立体几何中的信息加以合理迁移与融合,在考查空间想象能力的同时也传播数学文化。

三、立体几何中的判断问题

例3(多选题)图2 改编自李约瑟所著的《中国科学技术史》,用于说明元代数学家郭守敬在编制《授时历》时所做的天文计算。图中的,都是以O为圆心的圆弧,四边形CMNK是为计算所作的矩形,其中M,N,K分别在线段OD,OB,OA上,MN⊥OB,KN⊥OB。记α=∠AOB,β=∠AOC,γ=∠BOD,δ=∠COD,则( )。

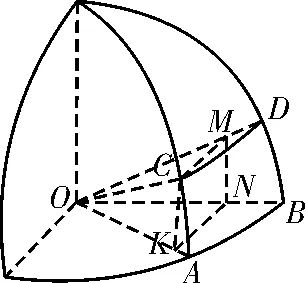
图2

点评:借助中国古代数学中的天文计算设置复杂的立体几何情景。解答该题的关键就是抓住立体几何的位置关系等来寻找相应的垂直关系,并利用三角函数的定义建立对应角的三角函数值的表达式,进而加以逐一分析与判断,实现立体几何中的对应元素的判断问题。

四、立体几何中的综合应用问题

例4刍甍是中国古代数学中的一种几何体,中国传统房屋的顶部大多都是刍甍。《九章算术》 中记载:“刍甍者,下有豪有广,而上有豪无广。刍,草也;甍,屋盖也。”翻译为:“底面有长有宽为矩形,顶部只有长没有宽为一条棱。刍甍字面意思为茅草屋顶。”如图3所示的五面体为一个刍甍,五个顶点分别为A,B,C,D,E,F,四边形ABCD为正方形,AB=2,EF∥平面ABCD,,平面BCF⊥平面ABCD,O为BC的中点。

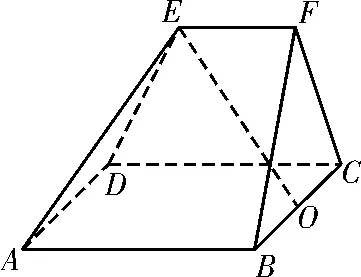
图3

(1)求证:OE⊥平面ADE。

(2)求平面ADE与平面BCF的夹角的大小。

(3)在线段AB上是否存在点P,使得直线FP与平面EOP所成角的正弦值为? 若存在,求出的值;若不存在,请说明理由。

解析：(1)取AD的中点为M,连接OF,OM,ME,由于EF∥平面ABCD,且EF⊂平面ABFE,平面ABCD∩平面ABFE=AB,所以EF∥AB。又OM∥AB,所以OM∥EF。因为,O为BC的中点,所以BC⊥OF。又BC⊥OM,OM∩OF=O,OM,OF⊂平面OMEF,所以BC⊥平面OMEF。又OE⊂平面OMEF,所以BC⊥OE。又BC∥AD,所以OE⊥AD。因为平面BCF⊥平面ABCD,OF⊂平面BCF,BC⊥OF,且平面BCF∩平面ABCD=BC,所以OF⊥平面ABCD。又OM⊂平面ABCD,所以OF⊥OM。在直角梯形OMEF中,OM=2,OF=1,EF=1,可得,所以OM2=OE2+ME2,则OE⊥EM。又因为AD∩ME=M,AD,ME⊂平面ADE,所以OE⊥平面ADE。

(2)如图4,以OM,OB,OF所在直线分别为x轴,y轴,z轴,建立如图4所示的空间直角坐标系O-xyz,则E(1,0,1),M(2,0,0)。

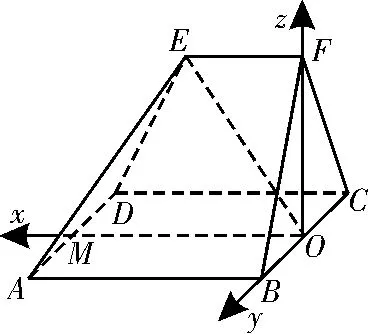
图4

所以在线段AB上存在点P,使得直线FP与平面EOP所成角的正弦值为,此时。

点评:借助中国古代建筑中的“刍甍”这一常见场景来合理构建立体几何情境,结合空间线面位置关系的证明、空间角的求解及存在性问题的确定等设置,来创设立体几何中的综合应用问题。合理数学文化场景的创设,融合中国古代建筑并结合立体几何中的相关知识加以应用。

依托立体几何这一基本场景,通过空间几何体的构建与应用,合理挖掘立体几何,交汇中国古代数学文化,融入立体几何的数学基础知识与基本考点,将数学知识中的“四基”巧妙融合与应用,合理实现对数学文化的渗透与数学文化的传播,有效增强同学们的理性思维与应用意识,培养同学们的爱国主义情怀。