宽幅钢桁梁桥面系构造特点及受力性能研究

陶重民

(1.安徽省交通规划设计研究总院股份有限公司,安徽 合肥 230088;2.公路交通节能环保技术交通运输行业研发中心,安徽 合肥 230088)

0 引 言

目前钢桁梁以其优异的刚度性能及可双层布置交通的特点被广泛运用于各类桥梁结构中,除了梁桥,斜拉桥、悬索桥和拱桥的桥面系也大量采用了钢桁梁桥面系,因此,对于钢桁梁桥面系的结构体系有必要做深入的研究。采用钢桥面的钢桁梁桥面系目前常用的结构体系主要有纵横梁体系和密横梁体系。纵横梁体系主要在桁架节点设置一道主横梁,主横梁间距随节间距变化在15 m左右,而在节间则仅设置刚度比主横梁减弱很多的横肋,部分横肋底板甚至在与主桁下弦相连的部位断开,以进一步削弱横肋的受力,将荷载更多由主横梁承担;在两道主横梁之间设置多道纵梁,其桥面系传力特点是:通过桥面板和纵梁将桥面荷载传递给主横梁,由主横梁将荷载传递给下弦杆节点,此时桁梁以承受节点荷载为主,少部分荷载通过横肋传递到下弦节间。采用这种体系的代表性桥梁有闵浦大桥[1-3]、三官堂大桥[4-6]和西洪大桥。

密横梁体系则不仅在桁架节点设置大横梁,在节间也设置刚度较大的横梁,横梁间距较密,通常为2.5～3.5 m,密布的大横梁使得纵梁的作用相对于纵横梁体系削弱很多,甚至可以取消纵梁,完全通过钢桥面板将桥面荷载就近传递给附近的横梁,由横梁将荷载传递给下弦杆。由于横梁较密且受力比较均衡,下弦杆也承受了一部分节间荷载,对于横梁高度不大且对横向刚度要求较高的情况,这种体系使用较多。采用这种体系的代表性桥梁有引江济淮繁华大道桥、铜陵长江公铁两用大桥[7,8]和杨泗港长江大桥[9]。

对于纵横梁体系的桥面系,主横梁的受力是整个体系的核心和关键,其主要影响因素是主横梁间距,即主桁节间长度,纵梁高度以及横肋高度。主桁节间长度直接影响了分配到主横梁的桥面荷载,而纵梁高度则影响到桥面荷载向主横梁的传递,横肋的高度影响到主横梁承重的比例,横肋高度增加到一定程度时,纵横梁体系受力即类似于密横梁体系,即横肋大幅分担了主横梁的受力。本文将通过对这三个参数的敏感性分析来研究其对主横梁受力的影响。同时,牛腿端横梁的受力也很关键,其截面并非对称,在竖向荷载作用下,产生了斜向弯曲作用,导致顶底板横向受力不均匀,几道腹板剪应力也不均匀,故本文还研究相应的放大系数乘以杆系模型的结果,以考虑这种不均匀性。

本文以某宽幅钢桁梁桥为例,在ANSYS软件中建立全桥精细化有限元模型,桥面系采用板壳单元,上弦杆和腹杆采用梁单元,调整主桁节间长度、纵梁高度和横肋高度来研究其对节点主横梁受力的影响;通过精细化板壳模型和杆系有限元模型的对比,研究牛腿端横梁的不均匀受力性能。

1 主横梁受力的参数敏感性研究

通过主桁节间长度(即主横梁间距)、纵梁高度、横肋高度等方面的参数变化,对节点横梁的受力进行详尽的对比研究。

1.1 主桁节间长度

从力学概念上来看,主桁架节间长度,也就是主横梁的间距,对主横梁的受力影响是比较大的。主横梁间距很大时节间传递到主横梁的荷载也较多,设置主桁节间长度分别为10 m、12.5 m和15 m三组变量,保持桁架高跨比不变,节间数和外形保持不变,横梁截面也保持不变,横肋间距和截面也不变,考虑横向六辆车加载,在基本组合作用下不同主横梁间距时主横梁底板最大横向应力和最大剪应力的对比见表1。

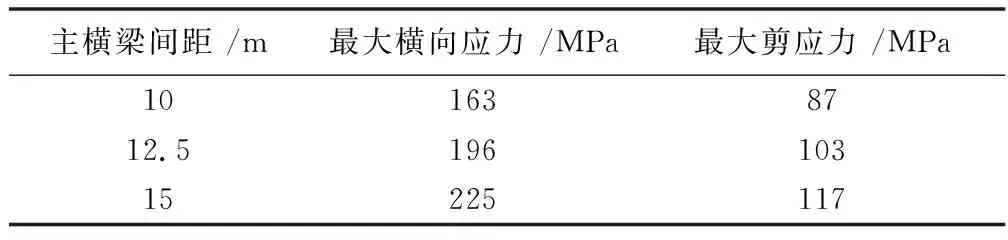
表1 不同主横梁间距时横梁最大正应力和剪应力对比

分析上述结果可知,主横梁主要承担了一个节间内的横向荷载,主桁节间长度越大,主横梁间距越大,横梁受力越不利,几乎是线性相关的关系。在设计中如果主桁节间长度较大,则应适当加强主横梁的截面或板厚。

1.2 纵梁高度

纵梁高度越大,主横梁之间的联系越紧密,在节间荷载的作用下,主横梁的受力也会受到影响。为此,设置了四组变量,纵梁高度分别为0.4 m,0.8 m,1.2 m和1.6 m,研究主横梁受力情况。其中纵梁高度仅为0.4 m只是一种理想工况,因为此时纵梁仅仅变成了一道加劲,对于荷载的传力和分配大大削弱,节间桥面系的受力变得非常不利。实际上对于这种主要传递节点荷载的纵横梁体系来说,一定刚度的纵梁是必要的。纵梁将节间的荷载传递给相近的节点横梁,以保证桁架以节点受力为主。考虑横向六辆车加载,在基本组合作用下,不同纵梁高度时主横梁底板最大横向应力和最大剪应力的对比见表2。

表2 不同纵梁高度时横梁最大正应力和剪应力对比

分析结果表明,随着纵梁高度的增加,横梁的受力有所改善。故保证一定刚度的纵梁是很有必要的,但纵梁刚度也不宜过大,一方面浪费材料,另一方面会增加桥面系的抗弯刚度,增加桥面系局部抗弯承担荷载的作用,而削弱桁架本身所承担的荷载。

2.3 横肋高度

桥面系的受力是按照刚度来分配的,节点横梁刚度较大,所以多数荷载都传递到节点横梁上来。而随着横肋高度的增加,横肋也逐渐承担起更多的横向荷载,与此同时,节点横梁的受力逐渐减少。设置了五组横肋高度的变量,分别为0.8 m、1.0 m、1.2 m、1.4 m和1.6 m,考虑横向六辆车加载,在基本组合作用下,不同横肋高度时主横梁底板最大横向应力和最大剪应力的对比见表3。

表3 不同横肋高度时横梁最大正应力和剪应力对比

分析结果表明,随着横肋高度的增加,节点横梁的受力逐渐减少。这是因为随着横肋高度增加,整个结构体系慢慢接近多横梁体系,更多的荷载传递给了横肋从而传递给下弦节间。

3 牛腿端横梁受力性能研究

牛腿端横梁不仅需要承受主桥上方的车辆荷载,通过牛腿还要承受引桥小箱梁的恒载和活载,所以其受力较为复杂,用MIDAS Civil建立全桥杆系有限元模型,考虑梁单元的第七自由度以充分考虑扭转作用,横向加载车辆轮载,施加荷载与ANSYS全桥精细化有限元模型相同,对比分析两种模型的计算结果,如图1所示。

图1 端横梁整体横桥向正应力分布

在ANSYS精细化有限元模型中,端横梁顶板在跨中靠近牛腿侧应力最大,端横梁底板在跨中远离牛腿侧应力最大,在竖向荷载作用下,牛腿横梁呈现出斜弯曲受力效应,这是由于牛腿截面本身并非对称截面,形心主轴也为倾斜的缘故,如图2所示。

图2 端横梁底板横桥向正应力分布

牛腿端横梁的三道高腹板(非牛腿内的低腹板)受力也不均匀,靠近牛腿的腹板受力较大,依次向外呈递减趋势,如图3所示。

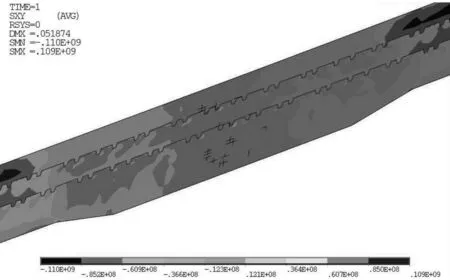
图3 端横梁腹板剪应力分布

在MIDAS杆系模型中,无法考虑上述效应,故所得应力均比ANSYS结果低,对比见表4。

表4 ANSYS与MIDAS模型牛腿端横梁最大正应力和剪应力对比

对比分析两种计算模型的差异可知,采用ANSYS板壳模型考虑了牛腿端横梁的斜弯曲效应,顶底板和腹板受力并不均匀,顶底板是杆系模型结果的1.35～1.4倍,腹板是杆系模型结果的1.25～1.3倍,设计中对于此类端横梁,应考虑到这种不均匀受力效应。

4 结 论

本文对纵横梁体系的钢桁梁桥面系进行了详细的对比分析,得到两点结论如下:

(1) 主横梁主要承担了一个节间内的横向荷载,主桁节间长度越大,主横梁间距越大,横梁受力越不利,几乎是线性相关的关系;一定刚度的纵梁对于纵横梁体系的钢桁梁桥面系很有必要,纵梁可以将桥面荷载传递到相近的节点横梁,保证桁架以节点受力为主;随着横肋高度的增加,节点横梁的受力逐渐减少。这是因为随着横肋高度增加,整个结构体系慢慢接近多横梁体系,更多的荷载传递给了横肋从而传递给下弦节间。

(2) 牛腿端横梁截面本身并非对称截面,形心主轴也为倾斜,其在主桥、引桥的竖向荷载作用下呈斜弯曲效应。端横梁顶板在跨中靠近牛腿侧应力最大,端横梁底板在跨中远离牛腿侧应力最大;牛腿端横梁的三道高腹板(非牛腿内的低腹板)受力也不均匀,靠近牛腿的腹板受力较大,依次向外呈递减趋势。ANSYS板壳模型考虑了牛腿端横梁的斜弯曲效应,顶底板是杆系模型结果的1.35～1.4倍,腹板是杆系模型结果的1.25～1.3倍,设计中应予以考虑。

本文对纵横梁体系的钢桁梁桥面系的受力特点的分析可为类似桥梁的设计提供参考,而对于其他桥型的牛腿端横梁设计,也应考虑到该处受力的复杂性和特殊性。