芜湖过江隧道掘进对长江大堤沉降影响研究

夏 琴, 商兆涛, 匡星晨, 张红彬, 王佐才

[1.芜湖市轨道(隧道)交通工程质量安全监督站,安徽 芜湖 241000;2.合肥工业大学 土木与水利工程学院,安徽 合肥 230009]

0 引 言

盾构法作为一种安全、环保、快速的全机械化施工方法[1],已经在我国的隧道建设中得到了广泛的应用。其中,城市过江过河隧道的建设大多数采用了大直径泥水盾构法来进行修建,在盾构掘进过程中不可避免地会引起地层损失和地表沉降,尤其是在穿越江河堤坝时可能会破坏其稳定性甚至发生坍塌事故,进而威胁到人民生命财产安全[2,3]。因此,研究盾构穿越大堤的沉降规律以及控制沉降的措施尤为重要。

近年来,对盾构掘进穿越堤坝扰动地层进而引起地表沉降的研究,业界已经积累了一定的经验。谢雄耀等[4]基于监测数据及数值模拟计算,对南京和燕路过江通道盾构穿越过程的各阶段对长江大堤的沉降规律进行了分析,并结合注浆压力等措施分析了控制沉降的有效举措。韩磊等[5]基于地层损失率的位移控制有限元法建立了浅覆土大直径盾构的三维模型,研究了地层损失率的参数与堤坝沉降的关系,通过对比监测数据,结果表明要想控制好堤坝的沉降就要将地层损失率控制在1%以内。吴昌胜等[6]通过对实测数据的统计分析,得到了大直径盾构隧道施工引起的地层损失率更小,分布更集中,并随着地层条件变好、渗透性变小而减小,同时中小直径盾构隧道引起的地层损失率与地层黏聚力、内摩擦角以及弹性模量呈负相关,与地面最大沉降呈一定线性关系,与覆土深度相关性较弱。以上研究主要是基于对现场监测数据的分析研究,为盾构穿越堤坝提供了相关经验。朱牧原等[7]结合监测数据对超大直径盾构隧道穿越黄河大堤所引起的坝顶沉降进行研究,分别对切口水压、注浆压力及大堤变坡段过渡方案对沉降的影响建模分析,结果表明,根据实际施工段调整切口水压和注浆压力以及优化施工过渡方案有利于控制沉降,但控制程度存在上限,当多种措施相互配合时能更有效地控制沉降。杨建刚[8]以上海沿江通道隧道工程为背景,采用有限差分法模拟了大直径隧道开挖对导堤的影响,结果表明导堤及开挖面加固可以显著提高整体结构稳定性。杨期祥[9]根据对成都地铁多个区间的施工断面实测沉降数据的处理,得到了成都砂卵石层的PECK修正公式,并得到了沉降槽宽度系数K与体积损失率η的变化范围,研究了地层性质对这二者的影响,最后得到了双线开挖的地表变形规律。上述基于数值模拟和经验公式的研究为大型盾构下穿堤坝工程的施工提供了很好的借鉴。

本文以芜湖城南过江隧道盾构下穿长江无为大堤为工程依托,利用有限差分软件FLAC 3D,在考虑土体开挖、泥水支护、管片衬砌、壁后注浆以及地层损失等诸多因素的基础上,对施工过程进行精细化模拟,分析压密注浆加固土体前后大堤的沉降,揭示大直径泥水盾构掘进过大堤时地表沉降的动态变化规律。

1 工程概况

芜湖城南过江隧道为安徽省第一条过江隧道,位于安徽省芜湖市长江皖江段“大拐弯”处,沿东西向布置,西起江北新城纬一路,东至江南主城的大工山路,距离下游的长江大桥约9 km,距离商合杭大桥约5.5 km。项目设计全长5.965 km,其中,采用开挖直径为15.07 m的泥水平衡盾构施工,左线盾构隧道段长3 957.77 m,右线盾构隧道长3 967.4 m,道路等级为城市快速路,双向六车道,设计最大速度为80 km/h,盾构隧道内径为13.3 m,外径为14.5 m,环宽2 m,车道高度为4.5 m,结构内净宽12.75 m,隧道最大纵坡为4%。

在始发后盾构向南掘进仅160 m即下穿无为长江大堤,无为长江大堤为长江重点保护大堤,防护等级高(图1)。穿越里程桩号为YK2+600～YK2+690,穿越长度约为90 m,大堤顶部距离隧道顶部为22.45 m。大堤地层顺序(自上而下)为素填土、粉质黏土、淤泥质黏土、粉砂、细砂、强风化粉砂岩以及中风化粉砂岩,无为长江大堤由素填土组成,对应的岩土层厚度依次为7.7 m、3.5 m、8.5 m、20 m、13 m、3.2 m、30 m。

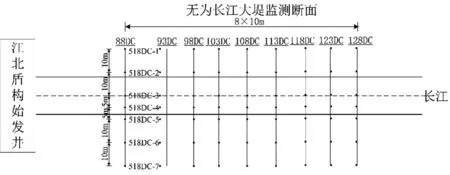
图1 盾构穿越无为长江大坝平面图

2 盾构穿越大堤数值模拟

2.1 数值模型及计算参数

2.1.1 模型尺寸、网格划分及边界条件

盾构穿越无为长江大堤采用泥水平衡盾构施工,隧道直径D为14.50 m,管片厚度为0.6 m。考虑到盾构隧道开挖扰动的边界效应,模型的宽度取9.8D,约为130 m,隧道底部距模型底部的距离不小于4.0D(约为53 m),双线中轴线相距20 m。计算模型边界尺寸为90 m(长度)×130 m(宽度)×78.2 m(深度),隧道顶部埋深为14.75 m,如图2所示。土层单元采用八节点六面体,模型单元总共276 844个,节点共290 285个。数值模型的边界条件设置如下:模型上表面为自由边界,四个侧面和底面均设置为法向约束。

图2 盾构穿越无为长江大堤段数值模型

盾构在穿越无为长江大堤段沿y轴向前推进,其中y=45 m的E-E剖面为堤坝顶部横向剖面,A-A剖面为其纵向剖面(图2)。假设盾构从洞口(y=0 m)向前推进的环数用n表示,对应的掌子面距E-E剖面为L,负号代表掌子面位于E-E剖面后方,当掌子面距E-E剖面为-15 m、-5 m、5 m、17 m、45 m和59 m时,对应的掘进环数分别为15、20、25、31、45和52环。

2.1.2 土体模型及其物理力学参数

根据工程地勘报告资料并参考相关工程经验,确定数值计算区域各材料的物理力学参数,如表1所示。力学模型选择摩尔-库伦弹塑性本构模型,将各地层弹性模量、黏聚力、内摩擦角等参数代入后进行初始地应力平衡。等代层、管片和盾壳均采用实体弹性单元模拟,其中等代层是将注浆层浆液与周围土层混合体等代为一种弱化土层来进行模拟。为了真实反映盾构内各组件的重量,需对盾壳等效厚度按盾构重度进行等效换算,换算后盾壳的计算参数为:E=200 GPa,v=0.30,γ=247 kN/m3。

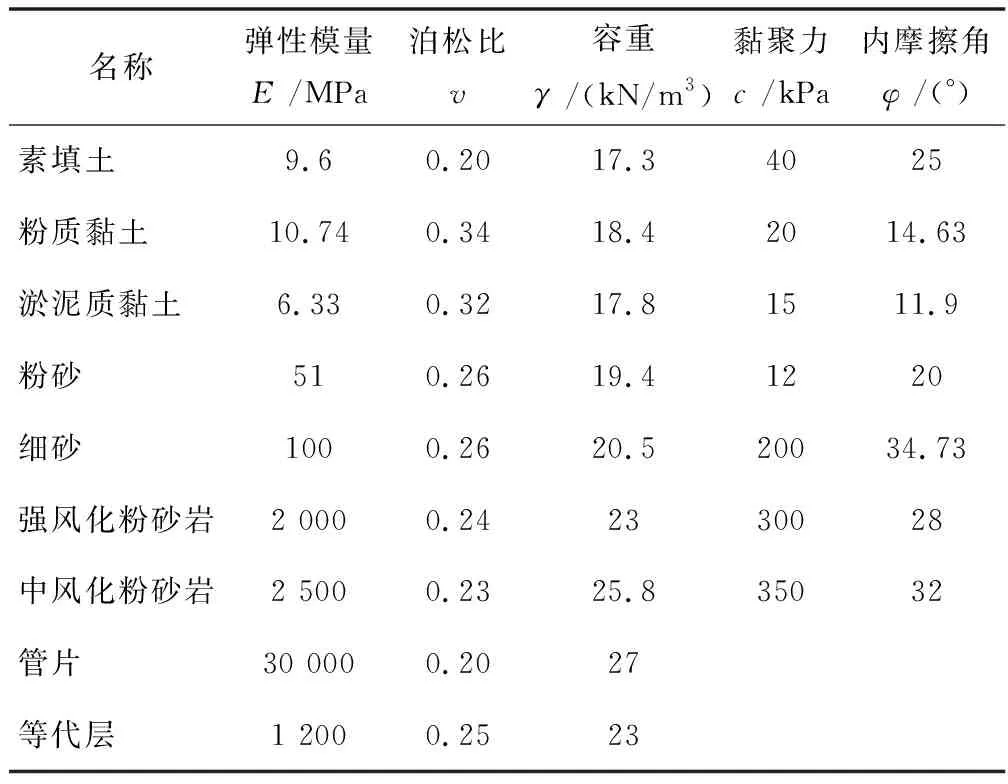
表1 土体及盾构施工主要物理力学参数

图3 试样制作

2.2 施工过程模拟

在芜湖城南过江隧道工程中,盾构管片宽度为2 m(即1环),而盾壳长度为15.60 m,盾构掘进过程单元宽度均为2 m。根据实际盾构施工过程,采用掌子面后7环管片长度来模拟盾壳单元的激活,2环管片长度模拟盾尾管片和等代层的激活,如图4所示。具体的模拟过程如下:

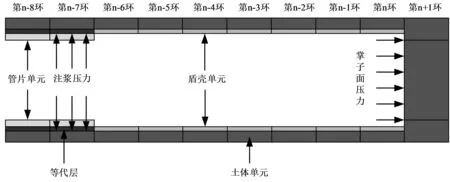
图4 盾构掘进过程模拟示意图

(1) 初始应力场的生成,即激活所有土层单元,计算模型的初始应力后将初始位移和速度清零。

(2) 第1环开挖,即洞门破除,此时盾构机尚未接触到开挖面土体,模拟时通过钝化洞门处单元来实现洞门破除。

(3) 第2环开挖,钝化第2环的隧道和管片单元,将掌子面压力施加在开挖面上,用盾壳单元替换此处的等代层单元。依次开挖到第7环,盾构机完全进入土体。

(4) 第8环开挖,钝化第8环的隧道和管片单元以及第7环的掌子面压力,第8环的盾壳单元替换为等代层单元,并将掌子面压力施加在开挖面上。然后激活第1环(洞门处)的管片和等代层单元,并施加注浆压力。

随着盾构的掘进,按照步骤4的方法,对不同部位隧道、管片、等代层及掌子面压力进行钝化或激活,直至盾构端头掘进施工完成。

本次模拟为了简化模型计算步骤,对部分条件进行如下假定:①为模拟刀盘削土体的过程,在计算的时候在开挖面上施加一定的表面力;②计算中不考虑衬砌管片分块之间的横向连接及各管片环之间的纵向连接对衬砌结构整体刚度的折减作用;③不考虑盾构施工过程中的盾尾空隙大小、注浆充填密实程度、隧道周围土体的扰动程度与范围;④假定盾构是一步一步的跳跃式掘进的,盾构每步的推进长度为2 m,为一个管片的长度。

3 结果分析

3.1 无为长江大堤加固措施分析

通过对无为长江大堤段土体进行压密注浆,由室内试验可知压密注浆使得注浆土体内摩擦角与黏聚力提高值为30%左右。在数值模拟中分别计算天然土体参数、土体参数提高10%、30%和50%四种工况下右线隧道盾构穿越无为长江大堤段对大堤地表的沉降影响(图5)。由图5可知,当右线盾构隧道在掘进至45环时,堤坝顶部横向E-E剖面的地表沉降呈现先增大后减小的趋势,呈抛物线分布,其中地表沉降的最大位置在右线隧道的中轴线位置,符合PECK[10]提出的地面沉降槽呈正态分布曲线。在未注浆的工况下,地表的最大沉降值为30.18 mm,在采取对土体进行不同程度压密注浆的加固措施后,地表的最大沉降值分别下降为27.90 mm、20.46 mm和16.67 mm。当土体参数提高30%后,地表沉降下降幅度达到了32%,满足了地表沉降标准,土体参数提高10%后地表沉降下降幅度7%,沉降值不满足要求,土体参数提高50%后沉降值满足要求但加固所需成本提高,故按照加固设计方案提出的注浆参数是合理的。

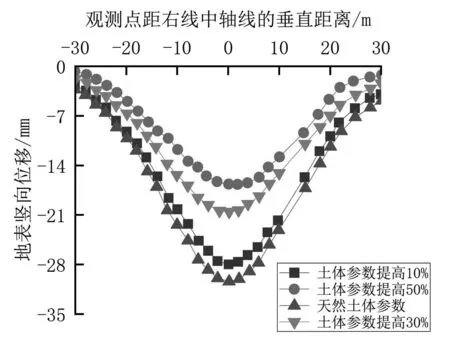
图5 右线在无为长江大堤段掘进45环时不同工况下E-E剖面的地表沉降曲线

3.2 右线掘进对地表沉降的影响

3.2.1 地层纵向沉降分析

为了进一步研究土体在压密注浆加固后,盾构穿越无为大堤段的开挖扰动效应,通过分析右线隧道在不同掘进环数时A-A剖面竖向位移云图进而获得地表沉降的规律(图6)。由图6可知,在开挖掘进的过程中,地表纵向的沉降区域以及沉降值都会随着开挖的进行逐渐增大,其中大堤底部的沉降区域及沉降值都是最大的,其主要原因是隧道顶部受到堤坝较大的重力作用,致使隧道的顶部出现了较大的沉降。隧道底部的隆起现象主要是由于随着开挖的不断进行导致土体卸载,原来的应力平衡被打破,使得盾构底部的土体不断向上移动。

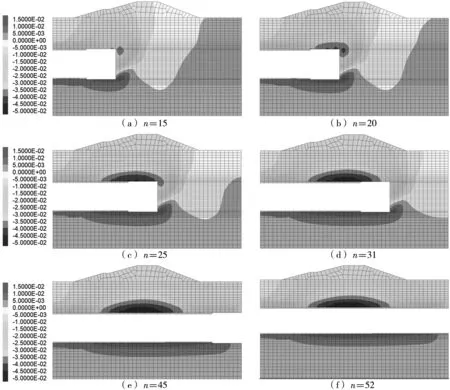
图6 右线在无为大堤段掘进不同环数时A-A剖面的竖直位移云图

图7为右线隧道在穿越无为大堤时不同掘进环数的竖向位移曲线图,并将模拟值与实测值进行了对比分析。由图7可知,在E-E剖面左侧的土体实测沉降值略小于右侧的沉降值,且实测沉降值趋于稳定值,而模拟值较实测值较大,模拟值的沉降趋势与实测值基本一致,能够大致反映土体沉降的规律。在盾构掘进到n=31环穿越堤坝顶部后沉降最大值在E-E剖面上,并随着开挖的继续进行沉降值增幅明显降低。

图7 右线在无为大堤段掘进不同环数时A-A剖面的地表沉降变化曲线

3.2.2 地层横向沉降分析

图8为右线隧道在穿越无为长江大堤段掘进不同环数时,E-E剖面的竖直位移云图。由图8可知,盾构施工掘进过程中地表横向沉降范围为40 m,约为2.8倍洞径,地表横向沉降区域沿右线中轴线呈对称分布,且随着掘进环数的增加,右线隧道顶部沉降区域不断向地表移动,右线中轴线处地表位移增加显著;当右线掘进环数大于45环后,地表横向沉降区域基本不变。

图8 右线在无为大堤段掘进不同环时E-E剖面的地表沉降变化曲线

图9为右线隧道在穿越无为长江大堤段掘进不同环数时,E-E剖面的位移沉降曲线。由图9可知,右线隧道掘进过程中地表沉降曲线呈先增大后减小的抛物线分布,且模拟沉降值均大于实测沉降值。当右线掘进15环时,模拟沉降值与实测沉降值吻合度较高,但随着右线掘进环数的增加,模拟沉降值与实测沉降值差异不断增加;当右线掘进45环时,右线中轴线处的最大模拟沉降值为20.46 mm,而实测沉降值为16.86 mm,增幅约为21%,而当右线掘进完毕(53环)时,右线中轴线处的最大模拟沉降值与实测沉降值分别为20.47 mm、15.67 mm,增幅为31%左右。上述结果表明,右线隧道在穿越无为长江大堤段掘进时,地表最大模拟沉降值大于实测沉降值,但两者均满足施工经验得出的地表沉降值,且模拟沉降值在一定程度上可以大致反映真实地表土体的变形规律,并为实际盾构施工设计提供参考。

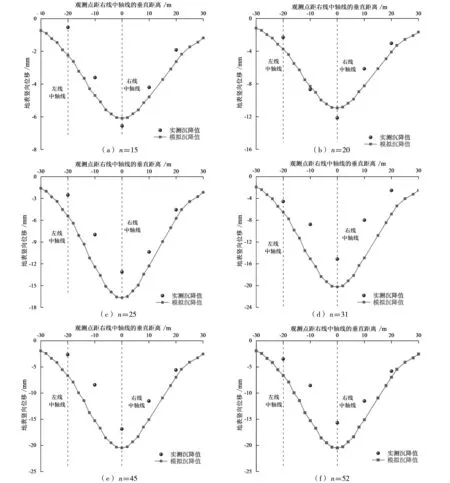
图9 右线在无为大堤段掘进过程中E-E剖面的地表沉降变化曲线

3.3 左线掘进对右线地表沉降影响分析

图10为左线在无为大堤段掘进过程中E-E剖面下地表竖直位移曲线。由图10可知,不同掘进环数下E-E剖面的地表沉降曲线均呈正态分布,当左线掘进环数小于15环时,地表沉降曲线关于右线中轴线对称,地面最大沉降值位于右线中轴线处,但随着左线掘进环数的增加,地表沉降曲线不断增加,且最大沉降值不断向左线靠近,当左线掘进环数为25环时,此时地表沉降曲线关于双线中轴线中间对称,并随着掘进环数的进一步增加,地表沉降曲线不变,此时地表沉降最大值为30 mm左右。

图10 无为大堤段左线掘进不同环数时E-E剖面地表沉降变化曲线

4 结 论

本文以芜湖城南过江隧道为例,运用FLAC3D有限差分软件对大直径泥水盾构机穿越土体注浆加固后的无为大堤段进行数值模拟分析,并将模拟值与实测值进行对比分析,得出的结论以及施工建议如下:

(1) 右线隧道在堤坝段掘进45环时,天然情况下堤坝顶部沉降值为30.18 mm,而采取压密注浆措施后堤坝沉降值仅为20.46 mm,降幅达32.2%,有效地降低了堤坝顶部沉降值,在盾构穿越大堤施工中对土体进行压密注浆可以作为一种有效的防止地表沉降的加固措施。

(2) 右线隧道在堤坝段掘进过程中,堤坝处横向剖面的模拟沉降值大于实测沉降值,且随着掘进环数的增加堤坝底部的沉降区域及沉降值不断增加,且符合PECK沉降槽,当掘进环数为15环时,模拟沉降值与实测值基本一致。在右线掘进完成后左线开挖对右线的影响分析中,左线掘进15环时,地表沉降曲线关于右线中轴线对称,而当左线掘进25环时关于双线中轴线中线对称,并随着掘进环数的增加地表沉降曲线不断增加,之后趋于稳定不变,此时地表沉降最大值为30 mm。

(3) 大堤在盾构穿越后的最大沉降值为20.46 mm,堤身高度为7.70 m,沉降值仅为堤身高度的0.27%,满足规范中沉降值不得超过堤身高度1%的保护要求。