小半径曲线双主梁钢板组合梁桥剪力滞效应研究

唐国喜, 邱体军

(安徽省交通规划设计研究总院股份有限公司,安徽 合肥 230088)

0 引 言

钢板组合梁桥由工字钢板梁与钢筋混凝土桥面板通过剪力键连接形成。这种组合结构充分利用了钢材和混凝土的材料性能,其具有承载力高、刚度大、抗震性能和动力性能好、构件截面尺寸小、施工快速方便等优点[6]。

清华大学聂建国等[1,2]等学者在2002年对钢混组合梁的受扭性能进行了一部分研究。研究主要针对的是不同加载方式对组合梁受扭性能的影响。胡少伟等[1]学者在2008年对总数为21根的组合梁进行分别为纯扭、弯扭、弯剪扭的有关试验。由于传统的钢板组合梁的整体性不够好,因此,关键联结部位的设计显得尤为重要。为解决传统的钢板组合梁的整体性不足问题,严加宝[3]提出了一种采用增强槽钢连接件的双钢板-混凝土组合结构,并对其进行了四点弯曲试验。程子涵[4]以某中等跨径钢板组合梁桥为背景,分别从荷载横向分布、整体稳定性及负弯矩区受力性能三方面对钢板组合梁桥的横向联结等关键受力问题进行了研究与探索。针对施工阶段钢板组合梁桥的受力性能,张华武[5]基于有限元模型计算分析,总结了钢-混组合梁桥的设计理论及验算方法,同时研究了钢-混凝土组合梁桥型在施工阶段和使用阶段的结构受力性能、施工性能、结构自重影响效应等方面。廖品博[12]分析了组合梁在顶推施工过程的受力,同时模拟了其在施工中的受力状态。

相比于传统的混凝土梁桥,钢板组合梁桥因自重轻而具有较好的抗震性能。胡章亮[7]基于Opensees和SAP2000有限元软件研究了支撑横梁体系钢板组合梁桥结构动力特性和地震响应规律特点以及对于不同设计参数的敏感度。张志威[8]基于SAP2000建立了钢板组合梁桥的抗震有限元模型,分析了梁和板刚度的变化对桥梁结构的动力特性的影响。

从以上分析可以发现,国内针对钢板组合梁的研究,主要集中在抗弯、抗剪和抗震性能上,而针对剪力滞效应的研究却不多。主要有邵真宝[9]应用能量变分法推导出双主梁钢板组合梁的剪力滞后效应基本微分方程,得到简支组合梁梁截面不同荷载工况下应力解公式。马天[10]对传统的钢板组合梁桥的剪力滞效应进行了研究,李兴坤[11]研究了波形钢腹板组合梁的剪力滞效应。而国内针对小半径曲线主梁钢板组合梁桥的剪力滞效应的研究十分有限,因此,本文以某高速公路匝道桥采用的小半径曲线双主梁钢板组合梁桥作为研究对象,分析了在恒载+车道外偏载情况下,曲率半径和计算跨径对于双主梁钢板组合梁剪力滞效应的影响,以期为该类桥梁的设计和施工提供借鉴。

1 项目概况

本文以某高速公路匝道采用的小半径曲线双主梁钢板组合梁桥为依托工程,取其中具有代表性的一联4×25 m跨径组合。其中,桥面板采用C50混凝土,箍筋采用HPB300,纵筋采用HRB400;钢主梁、端横梁、中横梁及小横梁均采用Q345工字直腹钢板,剪力钉采用ML15。钢板组合梁标准横断面如图1所示。该桥全长100 m,平曲线半径为250 m,混凝土桥面板宽10.5 m,高370 mm,混凝土桥面板和钢梁通过剪力钉连接,双主梁之间采用横梁加强横向联系,在全桥范围内等间距布置端横梁和中横梁,并在端横梁与中横梁之间等间距布置4个小横梁,桥梁支座布置形式如图2所示。

图1 桥面板标准横断面图

图2 支座布置图

2 有限元模型

本文采用ABAQUS软件平台建立了小半径曲线双主梁钢板组合梁桥的精细化非线性实体有限元模型,其中,混凝土材料采用塑性损伤模型;钢筋和钢材采用理想弹塑性模型。钢筋采用T3D2两结点线性三维桁架单元,其余部件均采用C3D8R八结点线性六面体单元进行建模[3]。模型假定桥梁中的剪力钉一直处于良好的工作状态,将剪力钉的剪力连接作用进行简化处理,从而直接将混凝土桥面板和钢主梁采用绑定接触进行连接,同时忽略钢筋与混凝土的相对滑移,将钢筋网直接内置在混凝土桥面板内部[3]。平曲线半径R=250 m的小半径曲线双主梁钢板组合梁桥有限元模型如图3所示。

图3 曲线双主梁钢板组合梁桥精细化非线性实体有限元模型

3 结果分析

采用小半径曲线双主梁钢板组合梁桥的精细化非线性实体有限元模型,分析了在恒载+车道外偏载情况下,曲率半径和计算跨径对于双主梁钢板组合梁剪力滞效应的影响规律。

3.1 曲率半径对剪力滞效应的影响规律研究

本小节主要探讨曲率半径对小半径曲线双主梁钢板组合梁桥剪力滞效应的影响,故在实桥的基础上,将平曲线半径从100～300 m每间隔50 m选取一个曲率半径,其他设计参数与实际桥梁一致,共建立了5个计算跨径为4×25 m、曲线半径不同的双主梁模型有限元模型。对比研究在恒载+车道外偏载组合作用下,关键截面的剪力滞系数分布特性,其中,关键截面分别为第一跨和第二跨间的支点(中支点1)截面、第二跨和第三跨间的支点(中支点2)截面、第一跨跨中(跨中点1)截面以及第二跨跨中(跨中点2)截面。

图4显示了在不同曲率半径情况下,两个中支点截面的剪力滞系数横向分布规律。分析图4可知,中支点处剪力滞效应随曲率半径的增大而增大,中支点1和中支点2在钢主梁处剪力滞系数最大相差9%左右。

图4 不同曲率半径下中支点截面的剪力滞系数横向分布规律图

图5显示了不同曲率半径情况下,两个跨中截面的剪力滞系数横向分布规律。分析图5可知,整体上剪力滞效应随着曲率半径的减小变得更加明显。不同曲率半径的剪力滞系数在两根钢主梁之间差异很小;在外侧钢主梁对应顶板处剪力滞系数随曲率半径的增大而减小,两截面最大相差分别为9.8%和10.9%;内侧则相反,且剪力滞系数均小于1。对比图5(a)和图5(b)可知,第二跨跨中截面的剪力滞效应比第一跨跨中截面更显著,表明在桥中部更需要注意剪力滞效应。

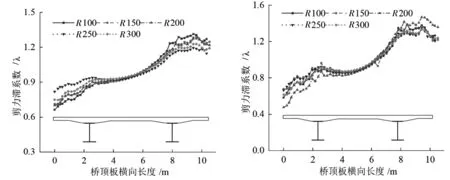
图5 不同曲率半径下跨中截面的剪力滞系数横向分布规律图

图6显示了不同曲率半径的曲线双主梁钢板组合梁桥剪力滞系数沿纵桥向的分布规律,沿纵桥向共取6个关键截面,其中,6.25 m处为第一跨四分之一截面,9.5 m处为第一跨上最大弯矩截面,12.5 m处为第一跨跨中截面,25 m处为中支点1截面,37.5 m为第二跨跨中截面,50 m为中支点2截面,且剪力滞系数取值为外侧钢梁对应的顶板剪力滞系数。分析图6可知,除中支点1外,剪力滞系数沿纵向整体上升,在各截面上曲率半径对剪力滞系数的影响规律并不显著。

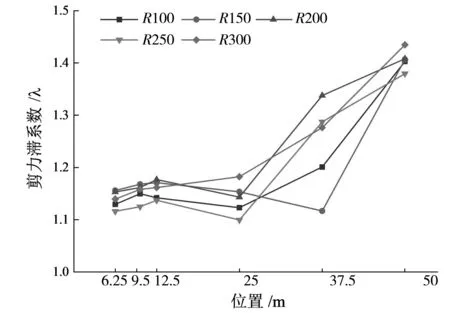
图6 不同曲率半径下剪力滞系数在纵桥向上的分布规律图

综上所述,曲率半径对中支点截面和跨中截面剪力滞效应的影响具有一定差异,中支点截面剪力滞效应随着曲率半径的增大而增大,而跨中截面则相反。剪力滞系数沿纵向整体上升,但在各截面上曲率半径对剪力滞系数的影响规律并不明确。

3.2 计算跨径对剪力滞效应的影响规律研究

本小节主要讨论计算跨径对小半径曲线双主梁钢板组合梁桥剪力滞效应的影响,故在实桥的基础上,建立4×20 m、4×25 m、4×30 m和4×35 m四种计算跨径且平曲线半径为R=250 m的小半径曲线双主梁钢板组合梁有限元模型,对比研究在恒载+车道外偏载组合作用下关键截面的剪力滞效应分布规律,其中,关键截面与3.1节中一致。

图7显示了不同计算跨径下剪力滞系数的横向分布规律,分析图7可知,剪力滞效应随计算跨径的增大而逐渐减小,计算跨径为4×20 m模型中支点1截面外侧钢梁剪力滞系数为1.58,比4×35 m模型大58%;计算跨径为4×20 m模型中支点2截面外侧钢梁剪力滞系数为1.72,比4×35 m模型大72%。中支点2截面比中支点1截面的剪力滞效应更为明显,各模型中支点2截面剪力滞系数平均比中支点1截面大10.9%。

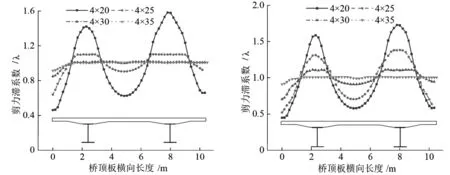
图7 不同计算跨径下中支点截面的剪力滞系数横向分布规律图

图8显示了不同计算跨径下跨中截面剪力滞系数的横向分布规律,分析图8可知,计算跨径较小的4×20 m和4×25 m钢板组合梁的剪力滞效应比4×30 m和4×35 m更加明显一些。在两跨跨中截面,内侧钢主梁剪力滞系数随着计算跨径的增大而减小,例如计算跨径4×20 m的内侧钢主梁剪力滞系数比4×35 m的分别大11%和28%。但是,第一跨跨中截面外侧钢主梁的剪力滞系数总体上随计算跨径的增大而增大,最大相差6.7%,第二跨跨中截面外侧钢主梁的剪力滞系数则随计算跨径的增大而减小,最大相差11%。对比图8(a)和图8(b)可知,第二跨跨中截面的剪力滞系数整体比第一跨跨中截面更大,平均大4.3%。

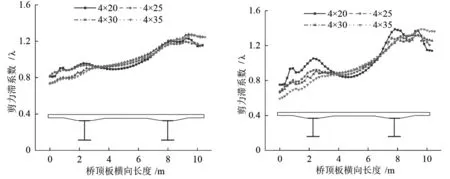
图8 不同计算跨径下跨中截面的剪力滞系数横向分布规律图

图9显示了剪力滞系数沿纵桥向的分布规律,其中,沿纵桥向共取6个关键截面,与3.1节中的图6一致。分析图9可知,除支点截面外,其他截面外侧钢主梁对应顶板剪力滞系数沿纵向逐渐增大;在同一截面上剪力滞系数随着计算跨径的增大而减小。

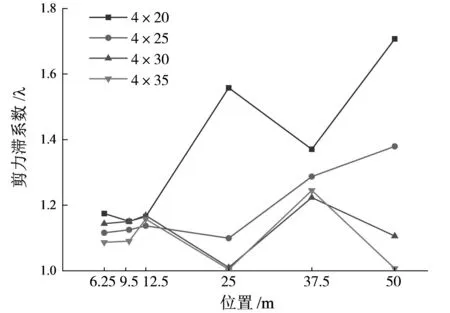
图9 不同计算跨径下剪力滞系数在纵桥向上的分布规律图

综上所述,在中支点截面,剪力滞效应随计算跨径的增大而减小。在跨中截面,内侧钢主梁剪力滞系数随着计算跨径的增大而减小,外侧钢主梁剪力滞系数则表现为边跨剪力滞系数随计算跨径的增大而增大,中间跨剪力滞系数随计算跨径的增大而减小,但规律性并不显著。在纵桥向,除支点截面外,其他截面外侧钢主梁对应顶板的剪力滞系数沿纵向逐渐增大;在同一截面上剪力滞系数随着计算跨径的增大而减小。

4 结 论

本文以某高速公路匝道桥采用的小半径曲线双主梁钢板组合梁桥为研究对象,分析了在恒载+车道外偏载情况下,曲率半径和计算跨径对于双主梁钢板梁剪力滞效应的影响,并获得主要结论如下:

(1) 曲率半径对支点截面和跨中截面剪力滞效应的影响具有一定差异,支点截面剪力滞效应随着曲率半径的增大而增大,而跨中截面则相反。剪力滞系数沿纵向整体上升,但在各截面上曲率半径对剪力滞系数的影响规律并不明确。

(2) 支点截面的剪力滞效应随计算跨径的增大而减小;在跨中截面,外侧钢主梁剪力滞效应随计算跨径的增大而增大,中间跨剪力滞效应随计算跨径的增大而减小,但规律性并不显著。在纵桥向,除支点截面外,其他截面外侧钢主梁对应顶板的剪力滞系数沿纵向逐渐增大;在同一截面上剪力滞系数随着计算跨径的增大而减小。

(3) 总体来说,对于多跨连续的小半径曲线双主梁钢板组合梁桥,中间跨的剪力滞效应比边跨要大。