双桥静力触探与土的压缩模量关系研究

苟联盟, 王 恒

(1.华设设计集团股份有限公司,江苏 南京 210014;2.江苏河海工程技术有限公司,江苏 南京 210022)

0 引 言

江苏省地貌单元[1]总体可划分为沂沭丘陵-平原区(Ⅰ)、徐淮黄泛平原区(Ⅱ)、里下河浅洼平原区(Ⅲ)、苏北滨海平原区(Ⅳ)、长江三角洲平原区(Ⅴ)、太湖水网平原区(Ⅵ)、宁镇扬丘陵岗地-平原区(Ⅶ)等七个地貌分区。江苏省内总体以平原地貌为主,其第四系地层分布广泛且厚度一般较大。第四系地层主要由淤泥及淤泥质土、黏土、粉质黏土、粉土、砂土及混合土组成,其主要成因有河湖相、河流相、湖沼相、滨海相、滨海浅海相、海陆交互相等。其土性特征得以使静力触探等原位测试方法得到大量应用。

1 既有研究成果

静力触探试验[2-4]是用静力将标准规格的锥形探头匀速压入土中,量测探头所受到的阻力,并据此估测土的力学指标和进行土层划分的一种原位试验;采用两个传感器和两个桥路,以分别量测探头端部所受阻力及探头侧壁所受阻力的探头称为双桥静力触探试验。

双桥静力触探试验适用的土层比较广泛,可用于软土、黏性土、粉土、砂类土及素填土等土层。

静力触探试验最早在1932年出现于荷兰,荷兰岩土力学奠基人Buisman曾建议[2],砂土的压缩模量ES与静力触探锥头阻力qc存在如下的关系式。

ES=1.5qc

(1)

式中:ES是固结试验求得的压缩模量,MPa。

公式(1)是由下列假设推出来的: ①触探头类似压进半无限弹性压缩体的圆锥;②压缩模量是常数,并且等于固结试验的压缩模量ES;③应力分布的Boussinesq理论是适用的;④与土的自重应力相比,应力增量很小。

我国在20世纪50年代引进静力触探试验,经过国内岩土人多年的研究,取得了很多成果。特别是对单桥静力触探试验比贯入阻力PS与压缩模量ES的关系总结出多个经验公式。

上述公式中鲜见采用双桥静力触探试验探头锥头阻力与侧摩阻力与压缩模量之间关系,而在土层地层定名划分中,双桥静力触探试验探头锥头阻力与摩阻比双指标应用已被证明其实用效果较比贯入阻力单指标更加可靠[2]。

本文以江苏省域内107个工程的现场双桥静力触探试验与钻探室内土工试验进行分析,以拟合固结试验求得的压缩模量Es与现场原位测试锥头阻力与侧摩阻力之间的关系。

2 数据分析

2.1 统计对象与主要土层指标

本文选取对象为江苏省内百余个工程项目勘察成果,以线路工程为主,含南京、镇江、常州、无锡、苏州、扬州、泰州、南通、淮安、盐城、连云港、宿迁等区域,包括各地貌分区的多地质成因黏性土,土性主要为淤泥质土、粉质黏土、黏土。各工程先进行原始土样分层统计,本次对各工程统计后的分层成果数据,按地层再汇总至本次样本数进行分析(表中样本数为各工程每个地质层的样本层数,实际试验数据远大于此),其典型参数如表2所示。

2.2 回归分析

我们对工程数据进行了汇总,并对各指标的相关性进行了初步分析,详见表3。

根据相关性分析结果,天然含水量、天然孔隙比、液性指数、压缩系数等指标与双桥静力触探试验探头锥头阻力qc、侧摩阻力fs之间呈负相关关系;质量密度、黏聚力、内摩擦角、压缩模量等指标与双桥静力触探试验探头锥头阻力qc、侧摩阻力fs之间呈正相关关系;其中压缩模量与锥头阻力qc、侧摩阻力fs的相关系数均大于0.8,相关性较高,有必要进一步进行研究。

依据上述工程的试验成果,分别作双桥静力触探试验锥头阻力qc、探头侧摩阻力fs与压缩模量ES的散点图(图1、图2)

图1 压缩模量ES与锥头阻力qc散点图

由图1、图2可见,压缩模量ES不仅与双桥静力触探试验锥头阻力qc相关性高,同时与探头侧摩阻力fs也有很好的相关性。

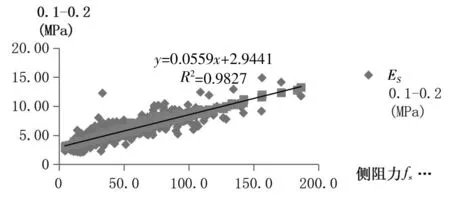
图2 压缩模量ES与探头侧摩阻力fs散点图

据此,我们采用多因子回归对压缩模量与双桥静力触探试验探头锥头阻力与侧摩阻力之间关系进行拟合分析,其回归关系式为:

ES=2.695+0.542qc+0.045fs

(2)

式中:ES为固结试验求得的压缩模量,MPa;qc为双桥静力触探试验探头锥头阻力,MPa;fs,双桥静力触探试验探头侧摩阻力,kPa。

回归拟合分析过程详见表4～表6。

表4回归统计中Multiple R自变量和因变量的相关系数,一般在-1～1,绝对值越靠近1则相关性越强,越靠近0则相关性越弱。该值在0.85以上表示高度相关,0.6～0.85表示显著相关,0.4～0.6表示低度相关,0.4以下表示不相关。

本次回归统计的MultipleR>0.85,表明压缩模量与锥头阻力与侧摩阻力两因子高度相关。

由表5可见,SignificanceF对应的是在显著性水平下的Fα临界值,即弃真概率。一般以<0.05为显著,<0.01 为非常显著。表中SignificanceF=1.6007E-123≪0.0001,故置信度在99.99%以上。

由表6变量系数及显著性检验可见,P-value对应统计学根据显著性检验方法所得到的P值,一般以P<0.05 为显著,P<0.01 为非常显著,P值越小越好。表6两个变量(两桥静力触探试验探头锥头阻力与侧摩阻力)的P值均≪0.01,故非常显著。

2.3 与单因子比对

同等样本数条件下,采用单因子回归对压缩模量与双桥静力触探试验探头锥头阻力之间关系进行拟合分析,回归统计分析见表7～表9。经拟合,其回归关系式为:

ES=2.69+2.04qc

(3)

单因子回归统计表7与采用多因子(探头锥头阻力与侧摩阻力)的回归统计表4对比,可见:

采用单因子锥头阻力与压缩模量的回归统计MultipleR值约为0.778,未达到0.85,表明压缩模量与锥头阻力为显著相关,尚未达到高度相关。

从而表明,压缩模量与双桥静力触探试验探头锥头阻力、侧摩阻力之间的回归关系式较单一指标探头锥头阻力的拟合情况好。

2.4 工程验证

以江苏省大丰疏港高速公路工程三标的实际详细勘察阶段双桥静力触探试验及土工试验数据进行验证,各地层物理性质指标见表10。

表1 PS(MPa)与ES(MPa)关系式

表2 江苏省黏性土主要物性指标及双桥静探参数

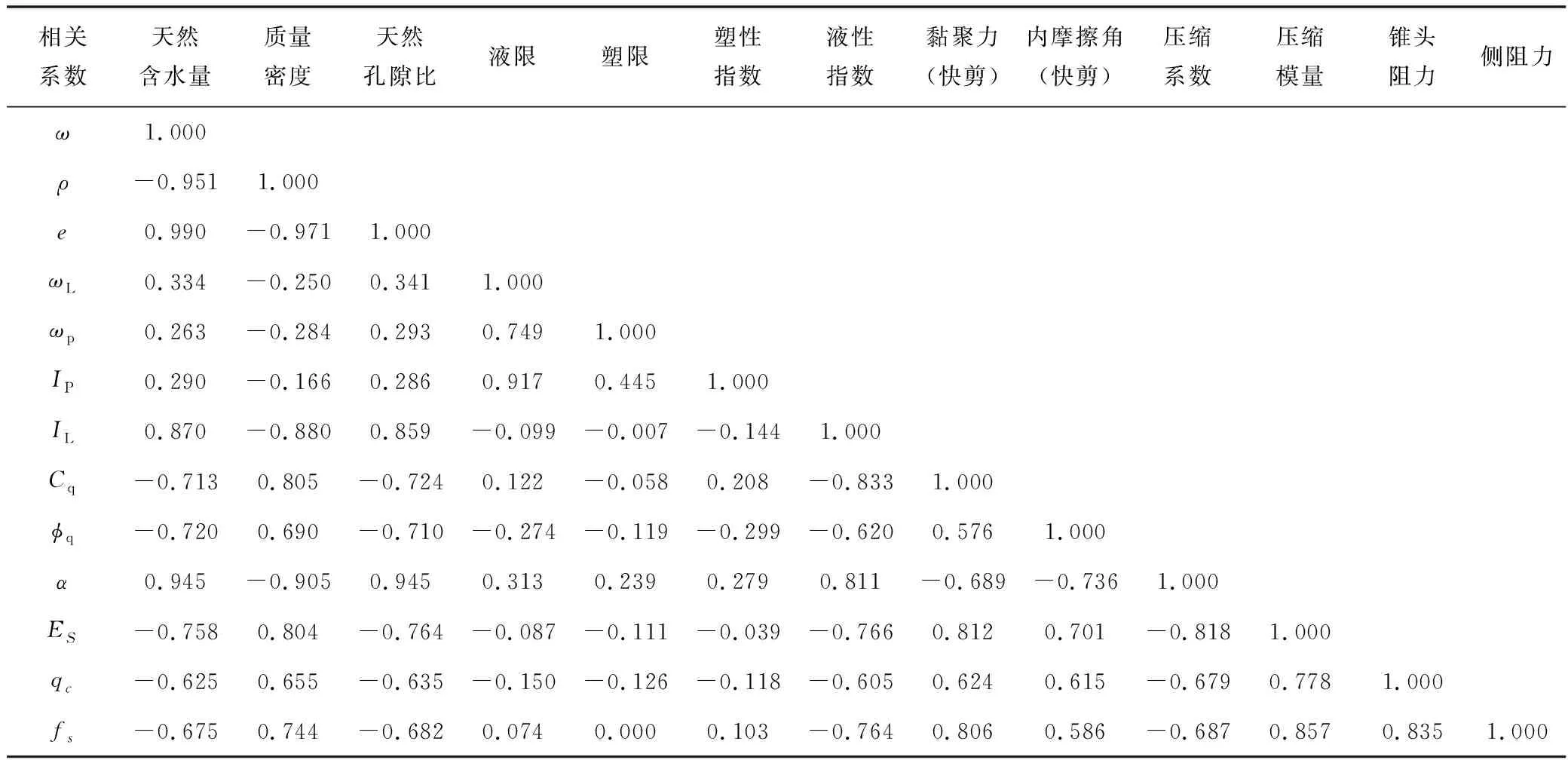
表3 各指标相关性分析

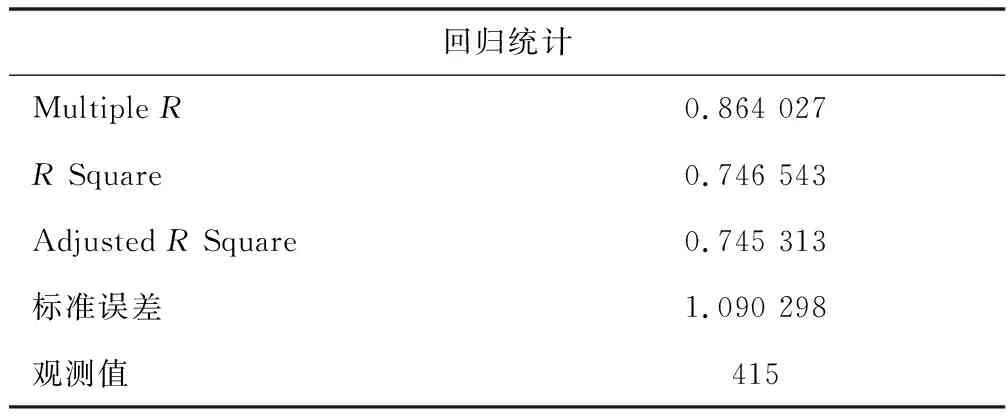
表4 多因子回归统计

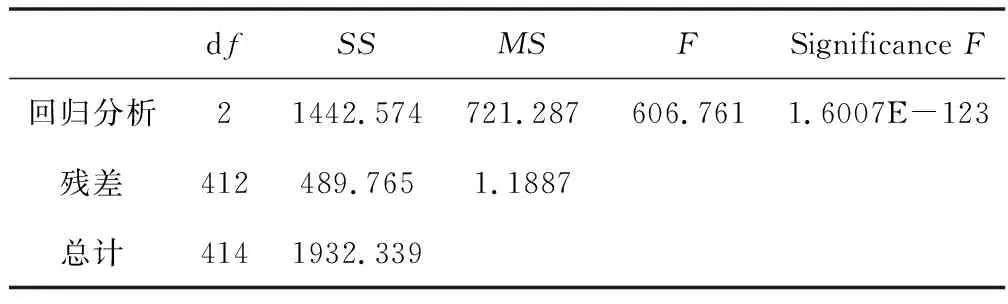
表5 方差分析

表6 变量系数及显著性检验

表7 单因子回归统计

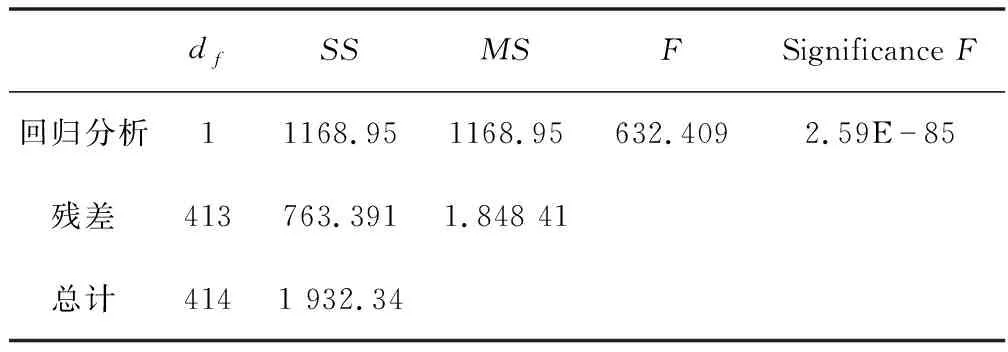
表8 方差分析

表9 变量系数及显著性检验

根据各层实测双桥静力触探试验结果,按压缩模量与双桥静力触探试验探头锥头阻力、侧摩阻力之间拟合公式(2)计算的压缩模量值及与试验值对比情况见表11。

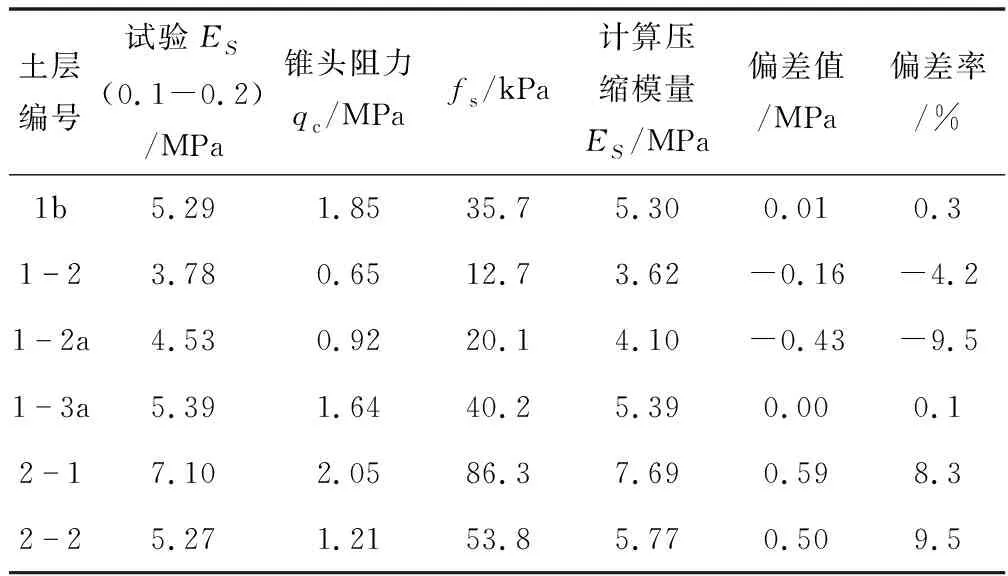
表11 探头锥头阻力、侧摩阻力计算压缩模量

采用压缩模量与双桥静力触探试验探头锥头阻力单指标拟合公式(3)计算的压缩模量值及与试验值对比情况见表12。

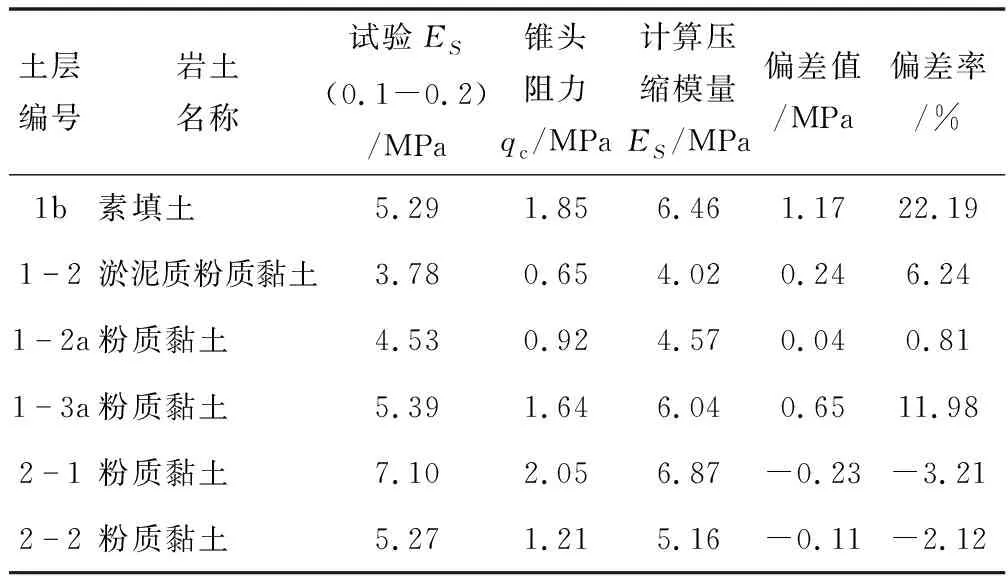
表12 双桥静力触探探头锥头阻力计算压缩模量

由表10、表11分析可见,采用锥头阻力qc单一指标拟合时,虽然有部分层位指标偏差率较小,但部分指标偏差率达11.98%～22.19%,采用双桥静力触探试验锥头阻力、侧摩阻力的拟合关系式计算的压缩模量与固结试验压缩模量偏差离散性较小,有较好的实用性。

3 总 结

3.1 小结

基于双桥静力触探试验在江苏省内的广泛使用,本文结合江苏省第四系地层各地貌单位及不同地质成因的淤泥质土、黏土、粉质黏土等黏性土双桥静力触探试验成果与其各层物理性质指标进行分析,重点对原位测试探头锥头阻力、侧摩阻力与室内试验的压缩模量之间的关系进行回归分析,得到以下主要结论:

(1) 对过回归拟合分析,黏性土压缩模量与双桥静力触探锥头阻力、侧摩阻力双指标高度相关,其相关性较压缩模量与双桥静力触探锥头阻力单一指标的相关性高,并得到其回归关系式。

(2) 通过对江苏省大丰疏港高速公路工程三标实际工程的分析计算,压缩模量与双桥静力触探锥头阻力、侧摩阻力的回归关系式得到较好的验证。

3.2 其他说明

(1) 工程上常常把地层锥头阻力qc<0.35 MPa时定义为淤泥;本文回归统计时,qc<0.35 MPa者数据偏少,此类土不建议采用此公式应用。

(2) 文中的拟合公式以江苏省内项目为依托,其他地区使用时应进行验证。