四个函数的单调性及应用

张志刚

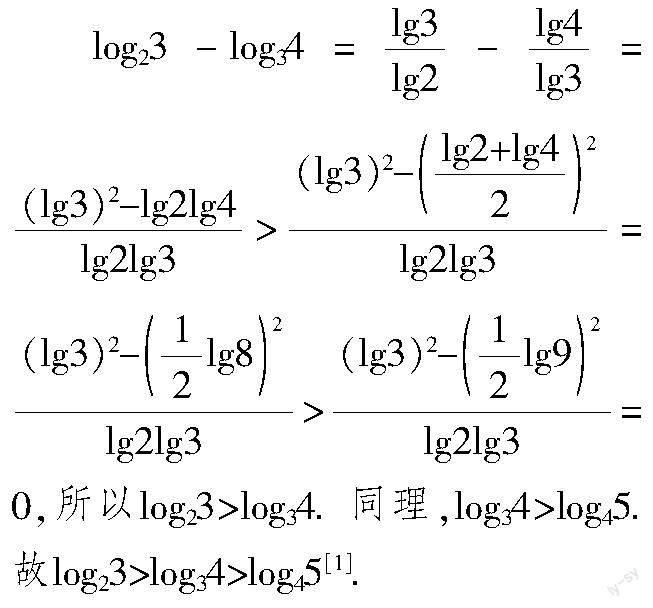
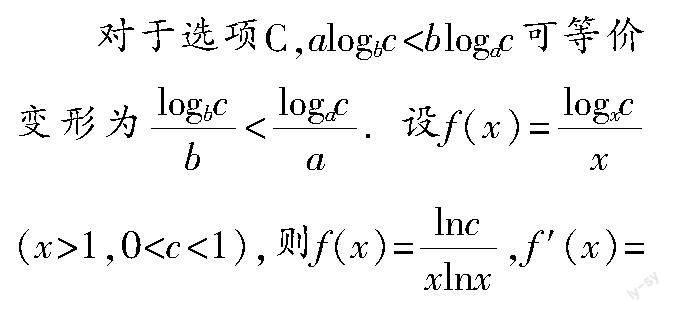
［摘  要］ 针对《普通高中教科书·数学必修第一册》（人教A版）中的一道比较对数大小的习题，学生提出构造函数利用其单调性解题的想法. 研究者引导学生对y=logxa，y=log（x+a），y=xlogxa，y=等函数展开探究，利用其单调性比较对数（式）的大小，为解题提供了新鲜视角.

［关键词］ 构造法；函数单调性；比较大小；类比推理

复习“函数与导数”模块时，笔者引领学生回顾《普通高中教科书·数学必修第一册》（人教A版）（下文简称“课本”）第141页的一道习题：

比较下列各题中三个值的大小：（1）log6，log6，log6；（2）log23，log34，log45.

两小问均比较底数互不相同的对数的大小，具有一定的思维难度.以第（2）问为例，先看教学用书的解答：

教学用书采用的是作差法：先利用对数换底公式将对数转化为常用对数，然后利用基本不等式等工具通过多次放缩完成大小比较.解答过程稍显烦琐.

对此有学生提出：在第（1）问中，三个对数具有“底数变化，真数为定值6”的结构特征，能否构造函数y=log6，根据其单调性判断大小呢？在第（2）问中，三个对数的底数和真数都在变化，且每个对数中的底数与真数均相差1，能否构造函数y=log（x+1），根据其单调性判断大小呢？

如此灵感，是在已有知识和经验的基础上展开丰富联想，实现思维正迁移的结果. 在“指数函数的图象和性质”的教学中，分析和解答“例3”时，学生学习构造函数y=1.7x和y=0.8x，利用函数的单调性判定两数的大小；在“对数函数的图象和性质”的教学中，分析和解答“例3”时，学生又学习构造函数y=logx和y=logx，利用函数的单调性判定两数的大小. 受此启发，学生类比联想到函数y=log6和y=log（x+1），利用其单调性解题，符合学生的思维规律和认知特点. 因此，笔者鼓励并协助学生对此深入研究，将函数y=log6抽象为y=logxa（x>0，x≠1，且a>0，a为定值），它不属于基本初等函数的范畴，是学生素未谋面的“新面孔”，如何研究它的单调性呢？将y=log（x+1）抽象为y=log（x+a）（x>1，且a为正常数），能否类似讨论它的单调性呢？

探索函数y=logxa的单调性

上述讨论过程综合应用了不等式的性质和代数式的变形公式等，而通过代数运算（变形）证明数学命题对学生而言是相对陌生的.除此之外，还有其他渠道可以考察函数y=logxa（a>1）的单调性吗？

我们知道，导数定量刻画了函数的局部变化，是研究函数增减、变化快慢、最大（小）值等性质的基本方法，因而也是解决诸如增长率、膨胀率、效率、密度、速度、加速度等实际问题的基本工具，是微积分的核心内容之一，还是现代数学的基本概念.在高中数学复习中，学生已经积累了利用导数探求简单函数的单调性等性质的活动经验，于是笔者打算引导学生用导数探究函数y=logxa（a>1）的单调性：

显然，当0<a<1时，f′（x）>0，则f（x）在（0，1）和（1，+∞）上分别单调递增. 可见，无论0<a<1还是a>1，函数y=logxa（x>0，x≠1，且a>0，a为定值）在（0，1）和（1，+∞）上具有相同的单调性.

例1 （2013年高考新课标Ⅱ理数第8题）若a=log36，b=log510，c=log714，则（  ）

A. c>a>b B. b>c>a

C. a>c>b D. a>b>c

交换例1的条件和结论，设计成例2.

例2 若实数a，b，c满足log2<log2<log2，则下列关系不可能成立的是（  ）

A. a<b<c B. b<a<c

C. c<b<a D. a<c<b

下面，继续用导数探求y=log（x+a）（x>1，且a为正常数）的单调性.

探求函数f（x）=log（x+a）的单调性

研究函数f（x）=xlogxa的单调性

函数f（x）=xlogxa（x>0，x≠1，a>1）的单调性也可以用来判定对数（式）的大小关系.

例3 （2017年高考全国卷Ⅰ理数第11题）设x，y，z为正数，且2x=3y=5z，则（  ）

A. 2x<3y<5z B. 5z<2x<3y

C. 3y<5z<2x D. 3y<2x<5z

当0<a<1时，可类似进行研究，如例4.

例4 （2016年高考全国Ⅰ卷理数第8题）若a>b>1，且0<c<1，則（  ）

A. ac<bc   B. abc<bac

C. alogbc<blogac   D. logac<logbc

解析 易知选项A，B错误.

追求解题过程由复杂到简单，追求思维过程由表及里、由浅入深，是数学工作者解题研究的一项基本任务.在解题教学中，教师要注重引导学生通过观察、实验、概括、联想、推理、证明、交流等思维活动，敏锐捕捉解题灵感，优化解题技能方法，增加题目的“附加值”. 尤其要注重培养学生的“质疑”意识，鼓励学生提出新想法、发现新规律、发展新理论.本文正是从学生的一个新想法出发，引领学生利用导数考察四个新函数的单调性，为判定对数（式）大小找到了统一简捷的解决之道. 当然，我们还要继续深入研究：函数的奇偶性、增长率（衰减率）、凹凸性等是怎样的？函数的图象是哪种形态的？在实际问题的解决中有何应用价值？

参考文献：

［1］ 人民教育出版社，课程教材研究所，中学数学课程教材研究开发中心. 普通高中教科书教师教学用书·数学·必修第一册（A版）［M］. 北京：人民教育出版社，2019.

［2］ 项武义. 基础数学讲义丛书：基础代数学［M］. 北京：人民教育出版社，2004.