输电线路分裂导线翻转自恢复特性研究

刘竹丽,胡俊涛,伍 川,张 博,邓 力

(1.郑州大学 机械与动力工程学院,郑州 450001;2.国网河南省电力公司 电力科学研究院,郑州 450052)

分裂导线翻转是指输电线路多分裂导线在外部载荷作用下某一间隔棒两侧导线相对扭转角度超过某一值时,导线产生多圈扭绞的现象[1],如图1所示。分裂导线翻转会在翻转间隔棒两侧形成一对扭绞区域,扭绞在一起的线路区间称为绞合区间。发生翻转的线路会极大影响线路的正常工作[2],由于其具有偶然性,除早期对实际事故的调查分析外,近年来针对分裂导线翻转问题的研究主要从分裂导线扭转刚度入手[3],通过搭建缩尺试验平台得到扭矩和转角之间的关系曲线[4],计算分裂导线的扭转刚度及失稳条件,来对线路进行防翻转强化。Nigol等[5]在一系列假设上推导了分裂导线扭转刚度的计算公式,通过测试得出在计算小档距时的分裂导线扭转刚度具有一定的精度,但在计算大档距时,误差会超过50%。Wang等[6-7]在Nigol基础上考虑了分裂导线由于扭转所引起的张力变化,提出了新的计算公式。Keutgen等[8]通过现场试验和有限元模拟,提出Nigol公式仅适用于小角度扭转的情形。谢增等[9]考虑了线路弧垂和两端高度差的影响,提出了一种计算分裂导线扭转刚度的新方法。马伦等[10]提出了一种计算相邻档及绝缘子串等效刚度的理论公式,该公式考虑了输电线上悬垂绝缘子串,同时包含了档距和高差等参数。姚文军等[11]对产生翻转的四分裂导线选择了停电、落地的修复措施。进行了导线翻转扭绞的力学、覆冰、场强影响的原因分析,分析认为是导线覆冰、雪引起线路舞动且导线张力松弛所致,并提出了相应的预防措施。史磊等[12]给出了带电处理六分裂导线翻转的措施,并进行了导线翻转扭绞的力学推导和现场条件原因的分析,提出避免导线翻转扭绞的几点预防措施与建议。刘小会等[13]推导了四分裂导线的扭矩对转角影响的理论公式,确定了导线张力和次档距是影响导线翻转的关键参数。

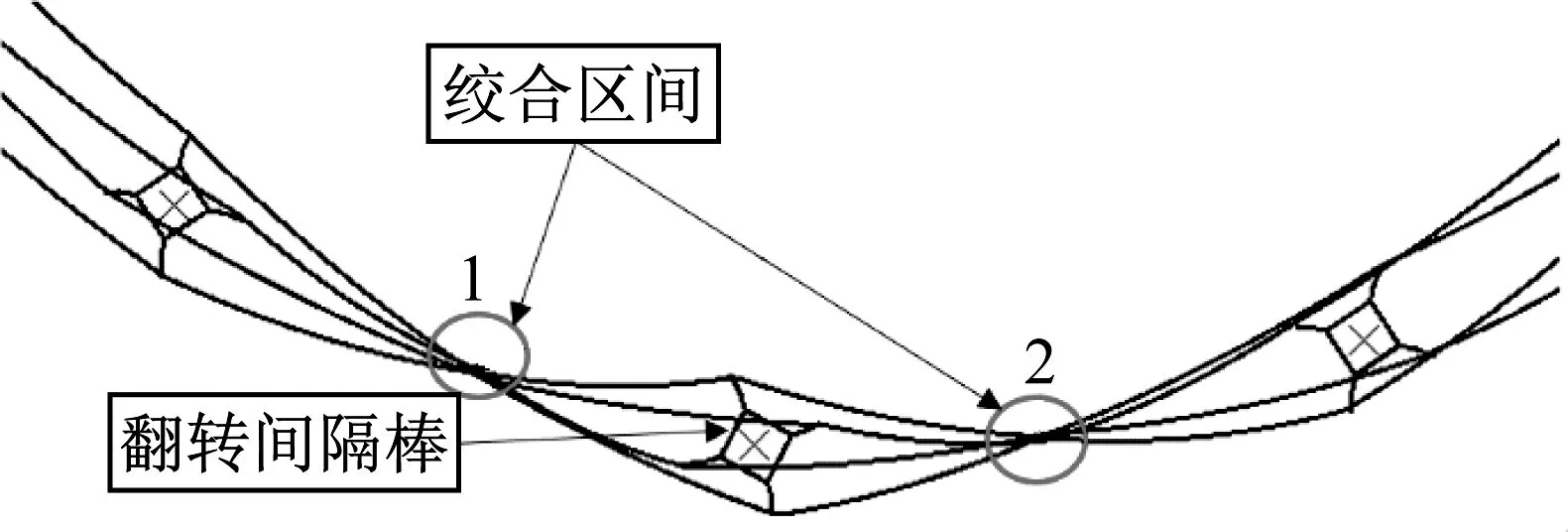
图1 分裂导线翻转示意图

以上研究主要集中在输电线路发生翻转的临界条件、翻转过程和翻转预防上,缺少对输电线路分裂导线翻转自恢复特性的研究。同时,分裂导线翻转前后结构变化较大,几何形状变化较为显著,利用翻转前分裂导线的状态无法准确描述分裂导线翻转之后的具体特性。因此在分裂导线翻转扭绞状态下,研究分裂导线翻转自恢复特性尤为重要。

本文将线路翻转后各子导线扭绞的状态特征和线路自身参数综合考虑,提出用线路自恢复力矩表征自恢复特性的简化理论计算公式,通过有限元分析验证公式准确性。根据简化理论计算公式,详细分析分裂数、绞合角度、次档距、分裂间距、绞合位置对分裂导线翻转自恢复力矩的影响。

1 分裂导线翻转自恢复力矩理论的建立

1.1 分裂导线沿线应力

输电线路中,一档内分裂导线通过绝缘子串悬挂并固定在输电杆塔的挂点上,在外界气象条件良好时,分裂导线仅受张力及自身重力。由于一档线路中分裂导线质量分布均匀、长细比较大,故可认为一档线的分裂导线呈悬链线形状[14]。

以等高单档线路导线最低点O点为原点,令x轴垂直于导线比载,y轴平行于导线比载,建立直角坐标系如图2所示。σ0为导线最低点应力,即导线的水平应力由导线的初始张力决定;γ为导线比载,即导线单位长度截面上的载荷。

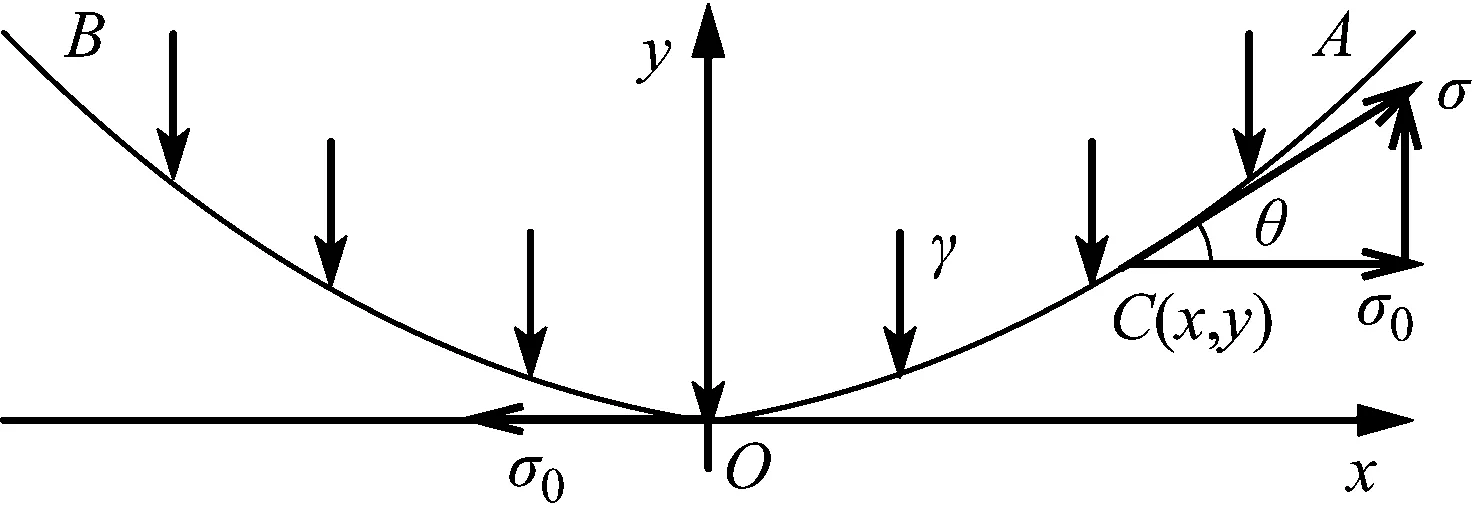
图2 等高架空导线受力示意图

根据悬链线的特征可知,导线上任意一点C纵坐标y可表达为[15]

(1)

式中,x为导线上任意一点C的横坐标,即C点到导线最低点的水平距离。

根据式(1),可求得导线上横坐标为x的点的斜率k(x)为

(2)

在重力的作用下,分裂导线上各处的水平应力大小处处相等且为σ0。分裂导线水平应力与竖直应力共同构成导线沿线应力σ,由图2可知导线上横坐标为x处的沿线应力σ(x)为

(3)

在一档线路中,导线的比载与初始张力不同,导线各个位置所受沿线张力大小也不同。

1.2 线路翻转扭绞后自恢复力矩理论计算

当线路发生翻转,两绞合区间的子导线通过圆周运动方式螺旋缠绕,翻转后绞合区间的导线段可视为圆柱螺旋线。根据图1,四分裂线路绞合区间1如图3所示,绞合区间中点称为绞合点,绞合区间的螺旋线半径为子导线轴线形成的螺旋线半径,用r表示。设子导线半径为rz,绞合区间长度为h,绞合区间两端子导线离绞点处螺旋角分别为ψ1,ψ2,绞合点位置不同离绞点处ψ1,ψ2不同。

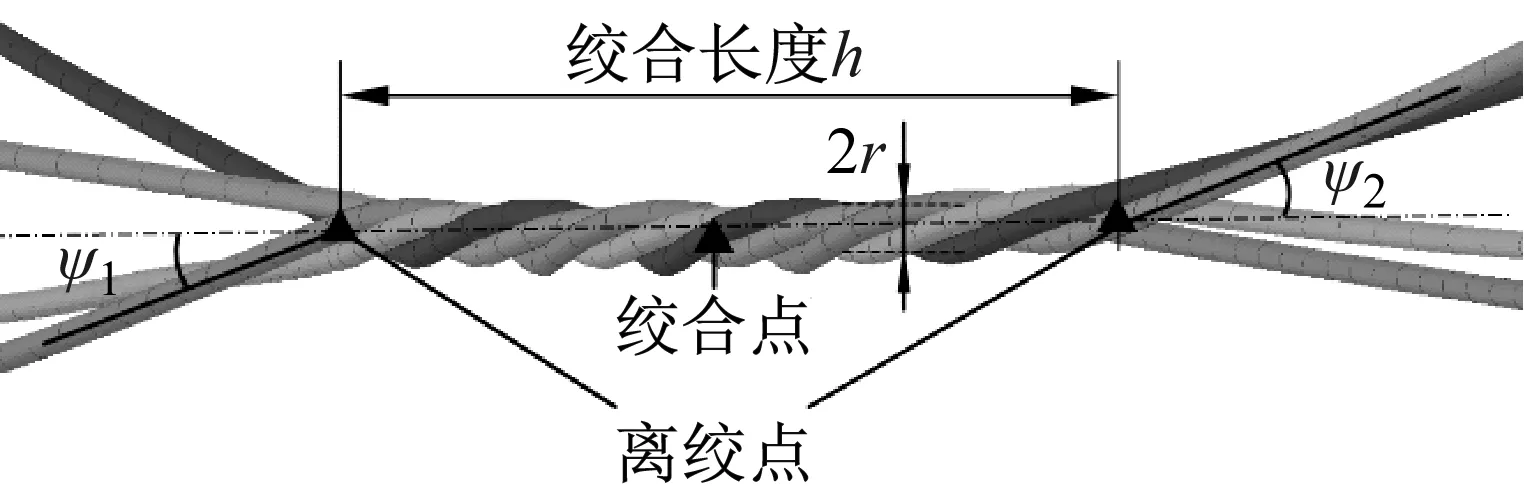
图3 四分裂导线翻转绞合区间示意图

1.2.1 绞合区间长度

根据螺旋线特征,子导线半径为rz的线路,其绞合螺旋线半径r与分裂数n有如下关系

(4)

根据绞合区间所在次档的几何特征,可假设绞合螺旋线的螺旋角由ψ1均匀变化至ψ2。若分裂线路翻转圈数用绞合角度α表示,线路绞合角度增大,绞合区间长度随之增加,绞合区间的长度h(α)可表示为

(5)

定义p为绞合点到翻转间隔棒距离与所在次档距长度l之比,其值在0～1,对绞合螺旋线的螺旋角ψ1,ψ2有影响。忽略分裂导线弧垂,建立绞合区间1到翻转间隔棒的几何与力学计算简化模型如图4所示。

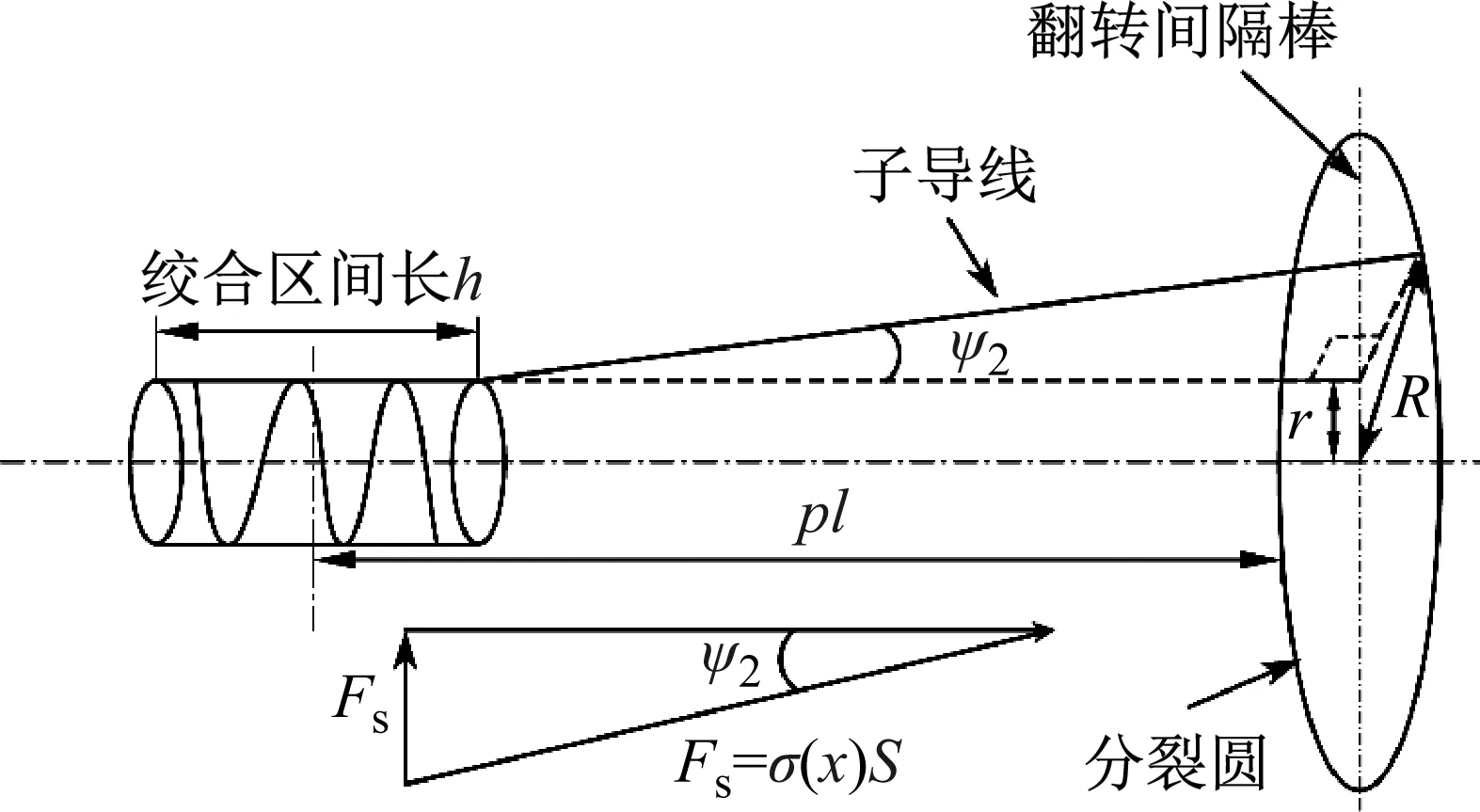
图4 分裂导线翻转几何与力学计算简化模型

根据几何关系,若线路分裂圆半径为R,发生翻转线路次档中绞合螺旋线离绞处的螺旋角为

(6)

由式(5)、式(6)可得绞合区间的长度h(α)为

(7)

线路翻转圈数越多,绞合角度α越大,绞合区间的长度越大。根据实际线路中观测数据,线路翻转圈数一般为1～4圈,即α在2π～8π。

1.2.2 线路翻转扭绞后子导线张力

根据图4的几何关系,绞合区间各离绞点到间隔棒的子导线段长度为

(8)

式中：j=1时,即ψ1侧离绞点,k=1-p;j=2时,即ψ2侧离绞点,k=p。

以ψ1侧离绞点为原点,将绞合螺旋线展开如图5所示,根据绞合螺旋线几何特征,其展开线为抛物线[16]。故图5中绞合螺旋线展开线的方程为

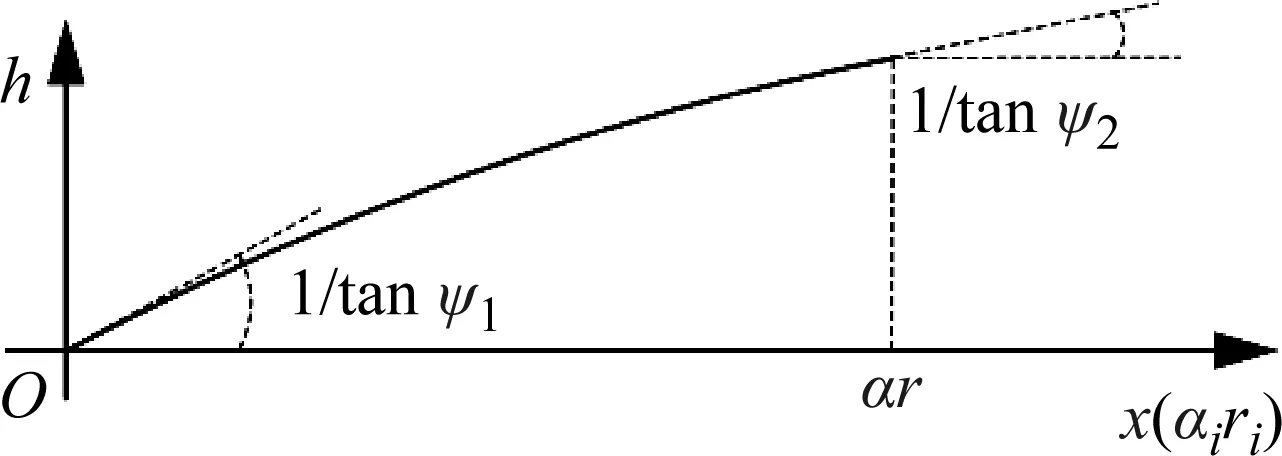
图5 绞合螺旋线展开示意图

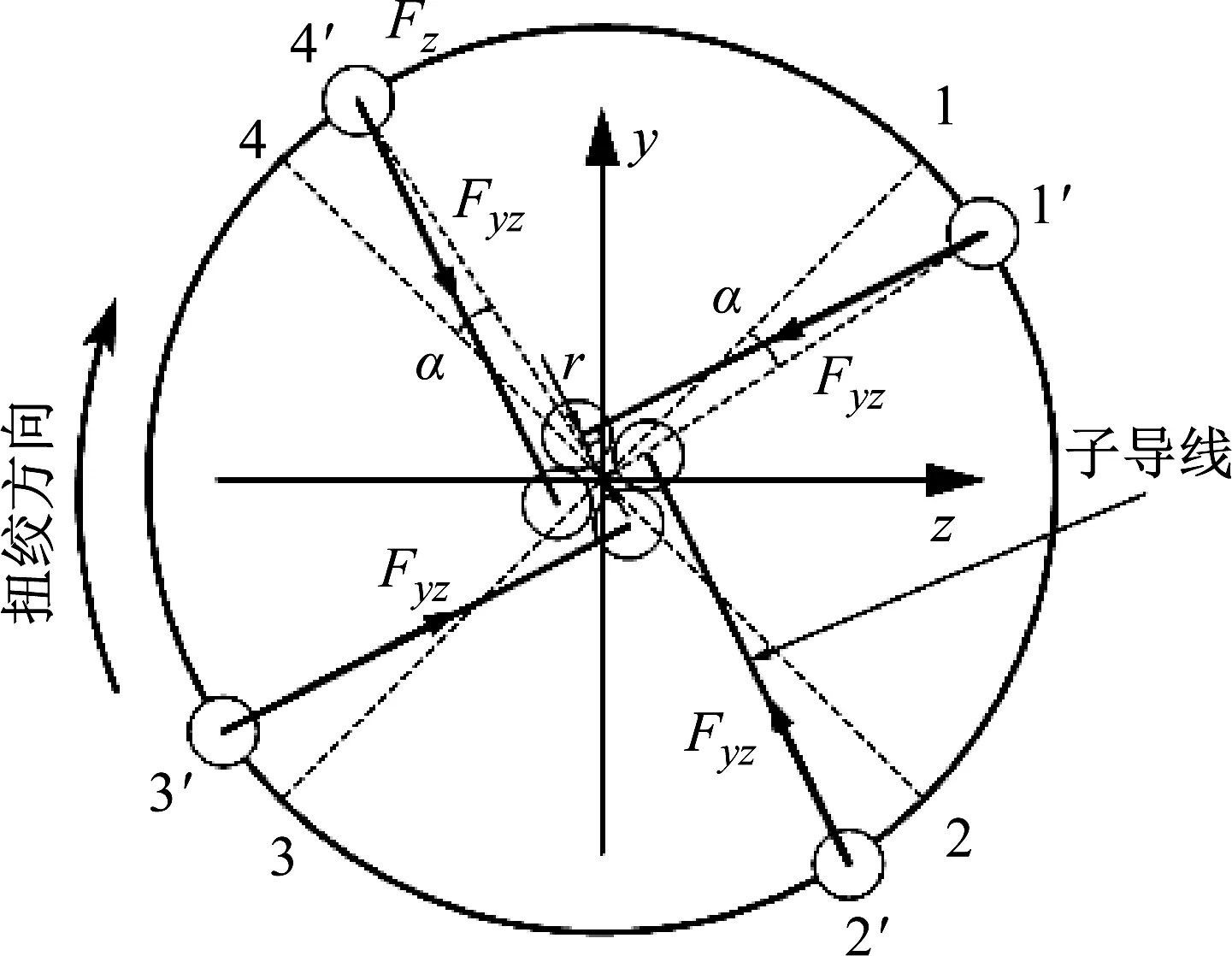
图6 翻转间隔棒单侧受力分析图

h=ax2+bx

(9)

其中

本文中绞合螺旋线为等直径螺旋线,故ri为常数与绞合螺旋线半径r相等,αi代表螺旋绕转角度为变量。则[0,αr]区间段螺旋线展开线即为绞合角度为α的绞合螺旋线展开线。

(10)

当ψ1=ψ2时,得出绞合区间的子导线段长度为

(11)

则线路翻转扭绞后绞合段子导线的总长度为

(12)

根据胡可定律,得到子导线截面积为S的线路翻转后翻转间隔棒处子导线张力为

(13)

1.2.3 翻转自恢复力矩简化理论计算公式

由图4可知,在等高线路中,翻转间隔棒受到子导线张力F在在竖直平面内投影Fyz大小为

(14)

忽略分裂导线弧垂,分裂导线的翻转间隔棒单侧受力分析如图5所示。由图5可知子导线对翻转间隔棒作用力矩等价于子导线对绞合螺旋线的作用力矩,故单根子导线翻转自恢复力矩Mi大小为

Mi(α,x,pj)=Fyzr

(15)

总翻转自恢复力矩M为所有子导线翻转自恢复力矩Mi之和,与翻转方向相反,因此,可以用总翻转自恢复力矩表征线路的翻转自恢复特性。两侧绞合区间不一定关于翻转间隔棒对称,故分裂数为n的线路翻转总翻转自恢复力矩M大小为

(16)

2 算例验证与分析

为验证线路翻转自恢复力矩简化计算公式的准确性,进行有限元仿真分析,并将计算结果及有限元结果进行对比。案例线路为：等高四分裂680 m档基本线路,分裂间距0.5 m,间隔棒型号为FJZ-445/300F,数量为7且均布排布,导线型号LGJ-300/40,案例线路工况参数如表1所示。

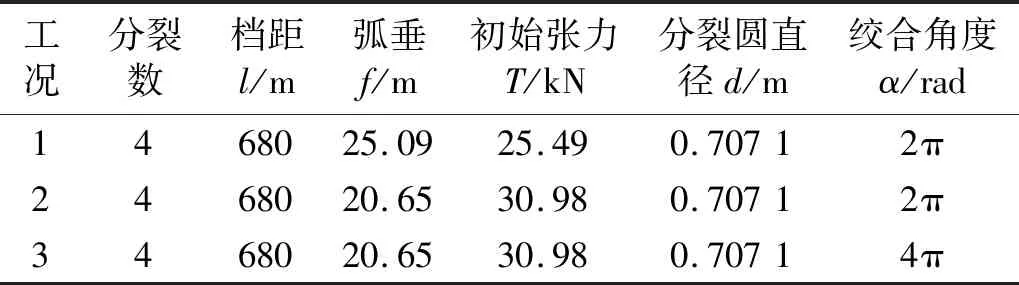
表1 案例线路翻转工况参数

2.1 有限元模型建立与验证

输电导线是非线性柔索结构,具有抗拉能力,一般忽略其抗压及抗弯刚度。通过释放两节点立方线性梁单元节点的弯曲自由度,将材料属性设置为不可压缩,建立自定义索单元模拟输电导线结构。间隔棒相对短粗且主要产生拉压、弯曲变形,故以两节点空间线性梁单元模拟。间隔棒与导线通过“Beam”类型的连接器连接。为准确模拟导线间翻转绞合现象,在子导线间添加切向滑动摩擦与法向硬接触,接触方式为边缘间接触。线路分裂导线两端固定约束。案例线路导线与间隔棒的材料属性由案例的导线、间隔棒型号查询标准确定,建立有限元模型[17]如图7所示,子导线网格数量为4 080,间隔棒网格数量为16。

图7 分裂导线有限元模型图

采用动力松弛法对导线初步找形,在档距中点的间隔棒上施加扭转角位移,间隔棒所受反作用力矩即为线路产生的扭矩。有限元分析的扭矩-扭转角关系曲线如图8所示,线路参数及工况1与解健等的研究相同,从计算结果来看,扭转角从0到2.43基本上为未翻转状态,该计算结果和解健等的研究结果基本一致,间接证明了本文建立的有限元模型的正确性和可靠性。

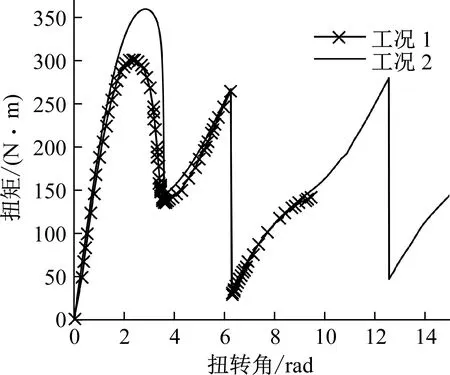
图8 有限元中扭矩与扭转角关系曲线图

由图8可知,工况2和工况1下的输电线路扭矩-扭转角关系曲线基本趋势一致。在工况1条件下,当线路即将发生翻转时,即线路扭转角到达2.35°左右,输电线路的扭矩到达第一个波峰。随着扭转角继续增大,此时输电线路整体结构失稳,次档中子导线逐渐靠近,输电线路的扭矩逐渐下降。当次档中子导线相互接触时,即线路扭转角到达3.65°左右,输电线路的扭矩到达第一个波谷。当扭转角继续增大时,次档中相互接触的子导线绞合程度增加,输电线路的扭矩逐渐升高。当线路的翻转绞合到达1整圈时,即扭转角为6.28°左右时,输电线路扭矩到达第二个波峰。当扭转角继续增大时,由于线路整体的扭转在两端固定约束的作用下会产生恢复,输电线路扭矩会产生突变,然后输电线路的扭矩会逐步增加直至下一个整圈时再次发生突变。导致扭矩突变的恢复属于翻转过程中线路整体产生的扭转恢复,本文研究输电线路翻转后绞合部分提供的自恢复能力,故取有限元分析中扭矩突变后较小值作为线路的翻转自恢复力矩。

2.2 分裂导线自恢复力矩对比分析

根据工况参数对案例线路分别进行有限元分析,得出工况1、工况2、工况3条件下绞合点到翻转间隔棒距离与所在次档距长度l之比p分别为0.470 3,0.481 5,0.411 5,并由式(16)计算得到对应工况下总翻转自恢复力矩。总翻转自恢复力矩计算结果如表2所示。

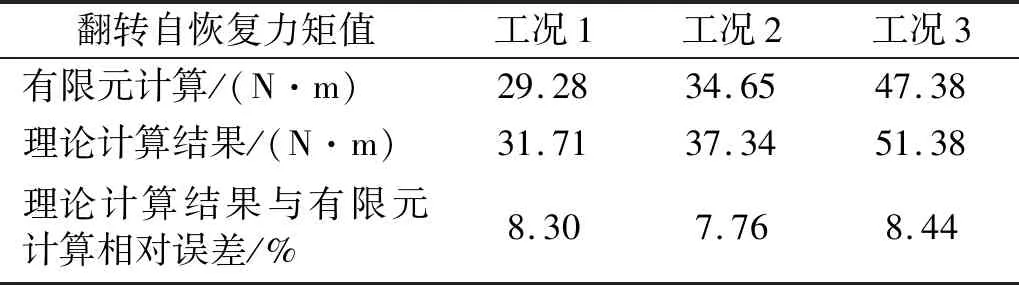
表2 总翻转自恢复力矩计算结果

工况1、工况2、工况3情况下,简化理论计算公式得到的线路总翻转自恢复力矩与有限元分析结果相对误差在可接受范围内。因此,可以认为本文提出的分裂导线翻转自恢复力矩简化理论计算公式对于分裂导线翻转自恢复能力的预测是准确可靠的。

3 本体参数对线路翻转自恢复力矩的影响分析

为了考察线路本体参数对翻转自恢复能力的影响,以第2章提出的案例线路为基础,应用简化理论计算公式进行分析,为线路设计提供参考。

3.1 次档距对线路翻转自恢复力矩影响

根据GB 51302—2018《架空绝缘配电线路设计标准》,实际运行线路中,分裂数不同线路分裂间距取值要求不同。在案例线路的基础上,p取为0.5,分裂数分别取2,4,6和8,对应分裂间距分别为0.4 m,0.5 m,0.45 m和0.4 m,分裂圆直径为0.4 m,0.707 1 m,0.45 m和0.482 9 m。各分裂数线路绞合角度在2π～8π内变化,次档距长度在40～80 m内变化,利用式(16)计算线路翻转自恢复力矩与绞合角度及次档距关系,结果如图9所示。

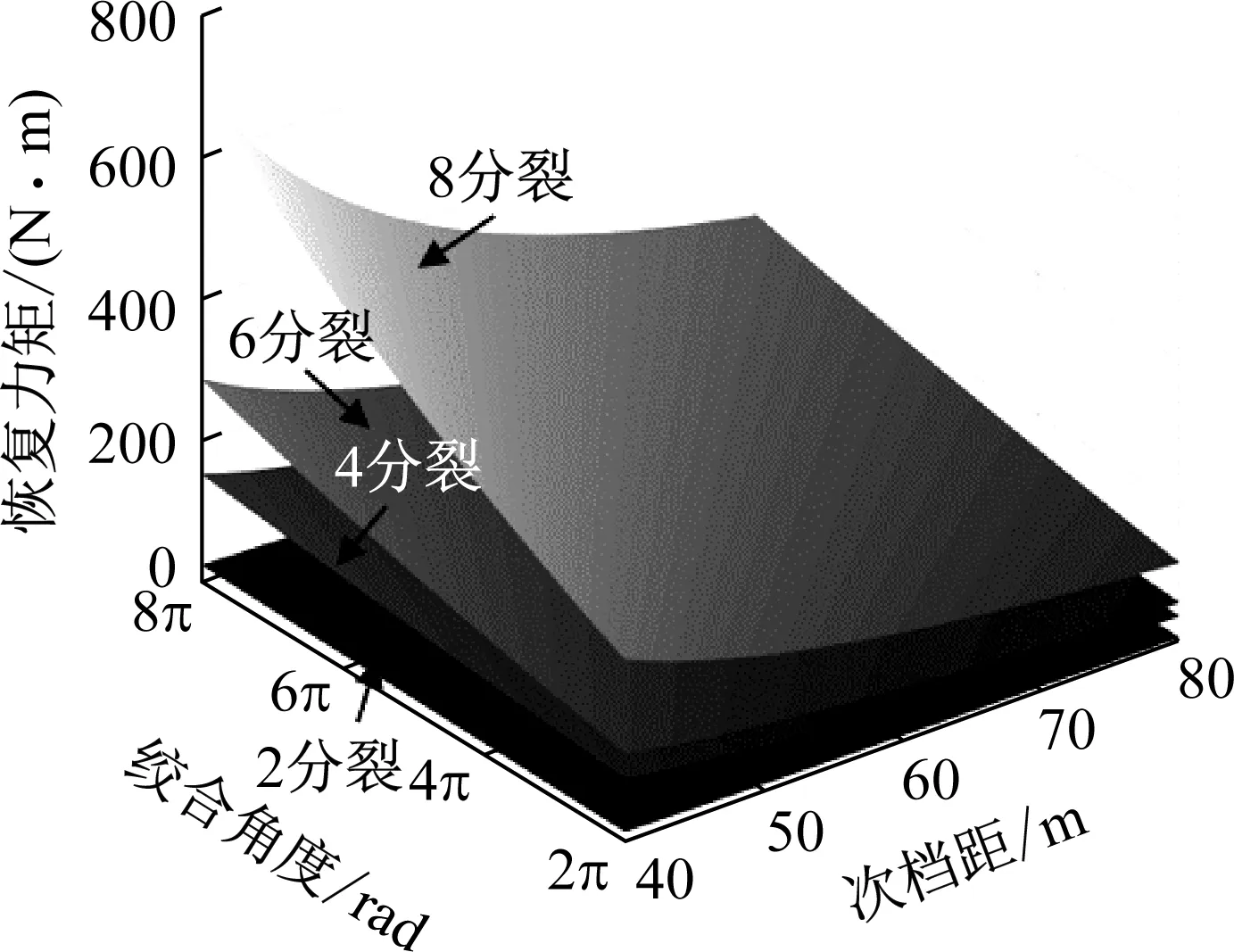
图9 分裂导线自恢复力矩与次档距关系图

由图9可见：对各分裂数线路,在绞合角度不变情况下,随着次档距的减小,线路翻转自恢复力矩增大;在次档距值不变情况下,随着绞合角度的增大,线路翻转自恢复力矩越大,线路自恢复能力越强。在上述参数范围内,绞合角度8π、次档距40 m时线路翻转自恢复力矩最大,绞合角度2π、次档距80 m时翻转自恢复力矩最小。线路的翻转自恢复力矩与导线分裂数关系密切,当线路其他参数一定时,线路分裂数越多,翻转自恢复力矩越大,次档距及绞合角度对翻转自恢复力矩的影响更显著。特别对六分裂线路,同等情况下翻转自恢复力矩远小于八分裂线路。

在线路设计中,多分裂线路选用较小的次档距长度、增加间隔棒数量,有利于增强线路翻转自恢复能力。特别对于易翻转地区六分裂导线,在GB 51302—2018《架空绝缘配电线路设计标准》要求下,要合理选用较小次档距长度以保证线路具有足够抗翻转能力。

3.2 分裂间距对线路翻转自恢复力矩影响

对各分裂数线路,分裂间距的大小决定分裂圆直径的大小,分裂圆直径不同会导致线路翻转自恢复力矩改变。在案例线路的基础上,取分裂数分别为2,4,6和8,p为0.5,绞合角度为2π,次档距为40 m。各分裂数线路分裂圆直径在0.4～0.8 m内变化,利用式(16)计算线路翻转自恢复力矩随分裂圆直径变化关系,结果如图10所示。

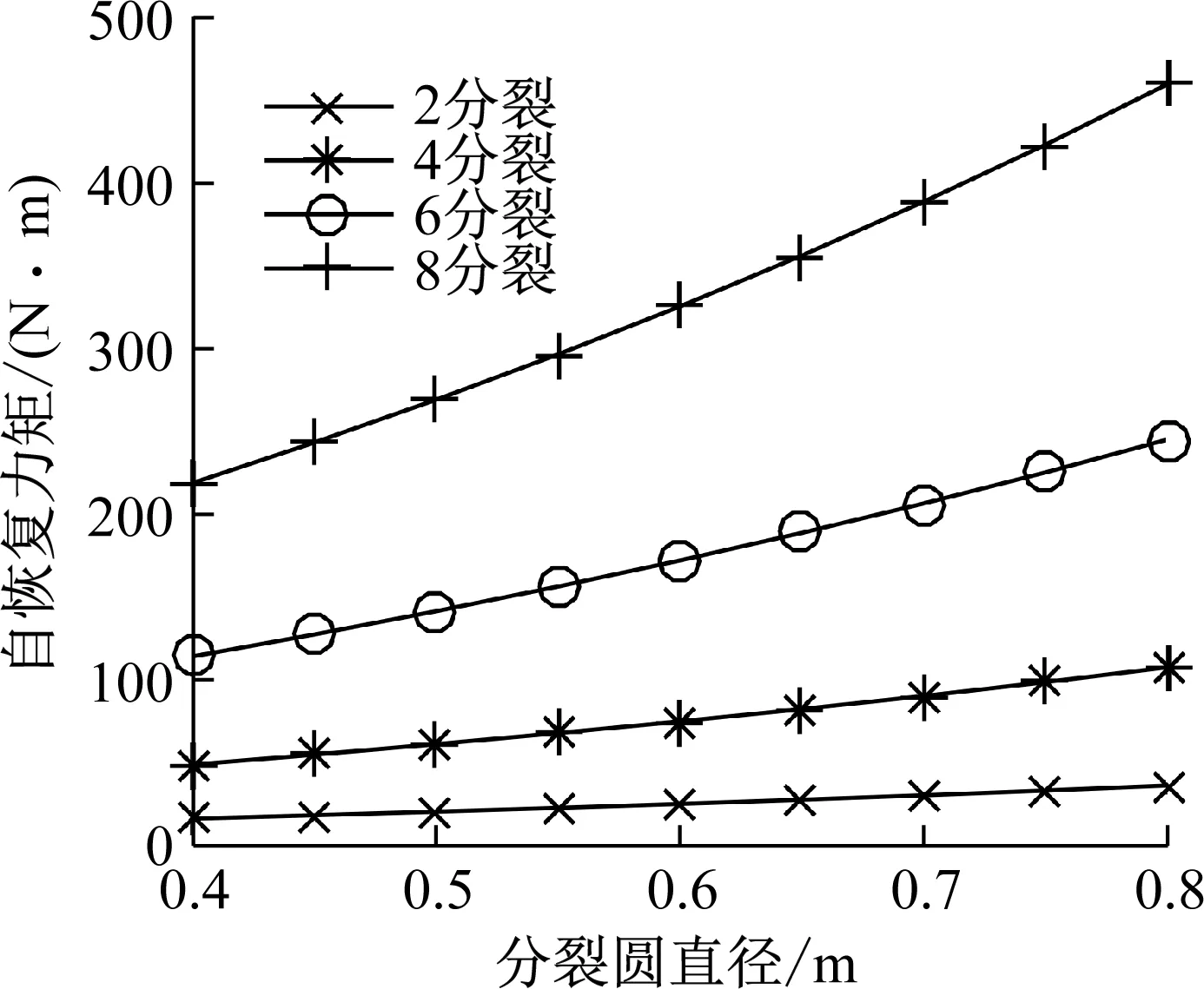
图10 分裂导线自恢复力矩与分裂圆直径关系图

由图10可见,对各分裂数线路,线路的翻转自恢复力矩与分裂圆直径整体呈线性关系。在同一分裂数下,分裂导线分裂圆直径越大,线路翻转自恢复力矩越大。随线路分裂数增加,线路的翻转自恢复力矩与导线分裂圆直径的比例系数呈倍数增大,4分裂、6分裂、8分裂导线的比例系数分别为2分裂导线的比例系数的2.9倍、6.4倍、11.7倍。分裂圆直径大小对八分裂导线的自恢复能力影响更大。

对各分裂数线路,适当增大线路的分裂间距,有助于提升分裂导线的翻转自恢复能力。由于不同分裂数线路的间隔棒挂点形成的几何图形不同,导致各分裂数分裂圆直径与分裂间距关系不同,相同分裂圆直径对应分裂间距不同。所以对于各分裂数线路,需要合理选用分裂圆直径确定分裂间距。

3.3 绞合位置对线路翻转自恢复力矩影响

在案例线路的基础上,绞合角度取为2π、次档距取为40 m,分裂数分别取2,4,6和8,对应分裂间距分别为0.4 m,0.5 m,0.45 m和0.4 m,分裂圆直径为0.4 m,0.707 1 m,0.45 m和0.482 9 m。p为绞合点到翻转间隔棒距离与所在次档距长度之比,其理论值在0～1。由于线路自身尺寸因素影响,p取值大多在0.3～0.7,p取值越小,表示绞合点距翻转间隔棒越近,反之则越远。故取各分裂数线p在0.3～0.7,利用式(16)计算线路翻转自恢复力矩随绞合位置变化关系,结果如图11所示。

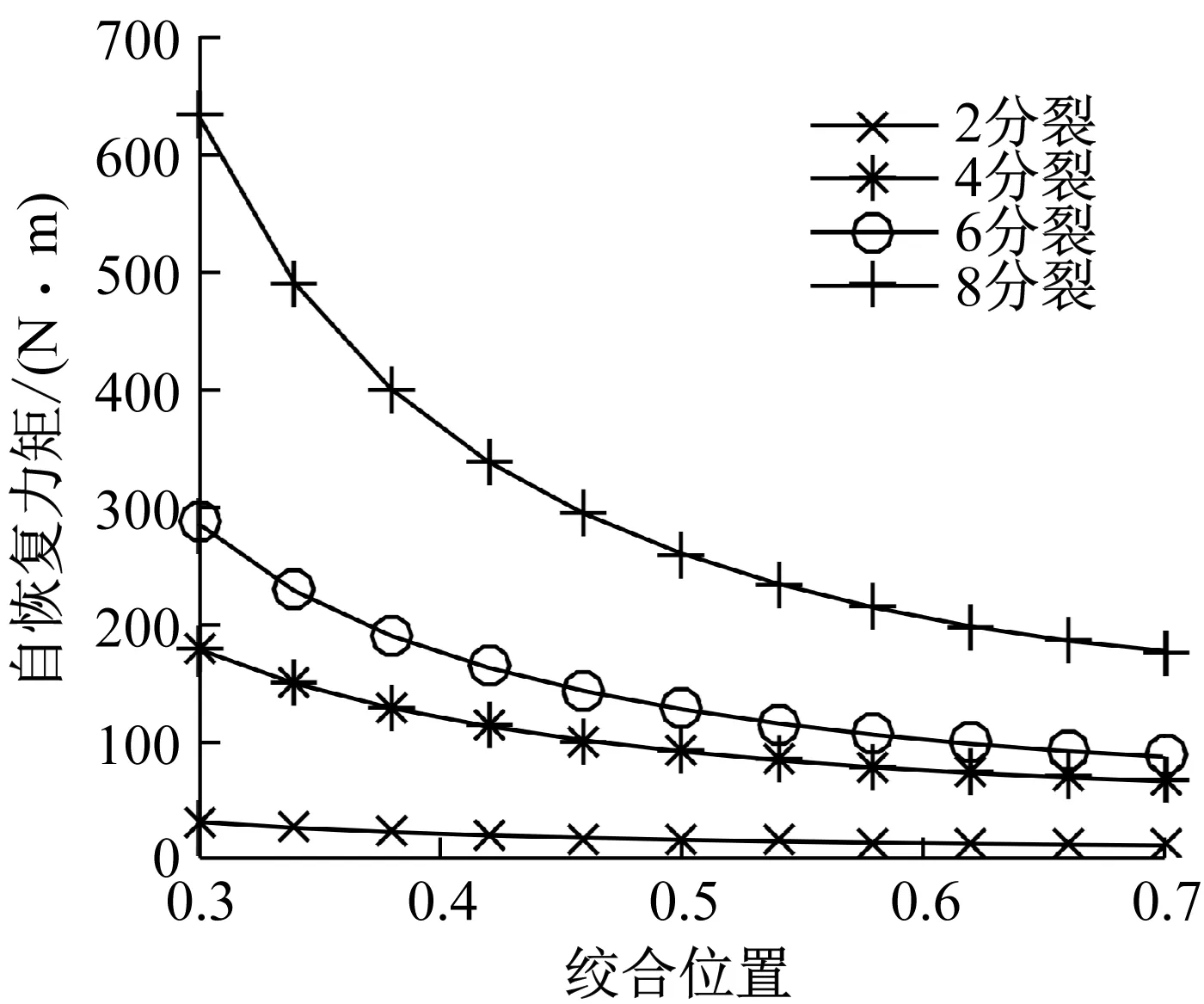
图11 分裂导线恢复力矩与绞合位置关系图

由图11可见,对各分裂数线路,线路的翻转自恢复力矩与绞合位置呈非线性关系。绞合位置越靠近翻转间隔棒p值越小,自恢复力矩越大,线路翻转自恢复能力越强,对翻转自恢复力矩的影响更显著。在上述参数范围内,分裂数越多,绞合点位置对自恢复能力的影响越大。尤其对于8分裂线路,绞合位置对翻转自恢复能力的影响最显著。

4 结 论

本文提出用线路自恢复力矩表征线路翻转自恢复特性,将分裂导线翻转后的绞合区间简化为圆柱螺旋线,建立了分裂导线的翻转几何与力学模型,推导了分裂导线翻转扭绞后子导线长度和张力,给出了分裂导线翻转自恢复力矩的简化理论计算公式。该公式能够明确影响线路翻转自恢复力矩的各种因素,便于研究各因素对翻转自恢复能力的影响。主要结论如下：

(1) 分裂导线翻转自恢复力矩简化计算公式结果与有限元仿真结果对比,3种工况下简化计算公式与有限元的相对误差分别为8.3%,7.76%,8.44%,相对误差在可接受的范围内,可以用来衡量线路在不同翻转程度下的自行恢复能力,为输电线路设计提供了理论依据和参考。

(2) 理论分析表明当线路翻转绞合角度增大,各分裂数线路的翻转自恢复力矩均有较明显增大。在一档线路中,翻转程度越剧烈翻转自恢复力矩越大,线路自恢复能力越强。

(3) 当输电线路分裂数越多、次档距越小、分裂间距越大、绞合位置越靠近翻转间隔棒时,线路翻转自恢复力矩越大,已翻转线路恢复原始状态的能力越强,线路发生翻转失效的概率越低。在环境和气象条件下易发生线路翻转地区的线路设计时,应该考虑适当增加间隔棒数量、增大分裂间距,可以有效降低线路发生翻转的概率。