水位变化对于移动荷载作用下土体动力响应的影响研究
姚锦宝,董隆华
(1.智能交通技术交通运输行业重点实验室,北京 100088;2.北京交通大学 土木建筑工程学院,北京 100044)
环境振动已经成为社会关注的热点问题,除施工及工业生产外,交通引发的环境振动问题对周围居民生活造成的影响最为严重。环境振动大多通过土体进行传播,因此研究移动荷载下土体振动响应对于交通所引起的环境振动问题十分具有指导意义[1]。
土体组成十分复杂,土壤性质差异极大,对波在土体中的传播精确模拟非常困难。Eason[2]采用积分变换方法求解了弹性波动方程解析解,研究了移动点荷载在3维匀质弹性半空间土体表面上的动力响应问题;Lefeuve-Mesgouez等[3]采用Foueier变换求解了垂直移动简谐荷载作用在2维弹性半空间上的振动传递问题,给出了不同速度和振动频率下地表位移响应的数值结果;Andersen等[4]在局部坐标系下推导了在移动简谐荷载作用下弹性介质稳态响应的3维边界元公式,求解出移动坐标系中位移和表面应力的时域基本解;Galvín等[5]采用3维时域边界元法分析了高速移动荷载下弹性土体振动,可用于实际分析高速列车所产生的振动。
对于饱和土,Biot等[6-7]首先提出了孔隙流体填充土骨架的两相介质弹性动力学理论,对固-液两相介质的惯性耦合、黏性耦合、弹性耦合进行了详细阐释;Theodorakopoulos等[8]利用Fourier级数展开法,考虑流-固耦合作用,对平面应变条件下矩形荷载作用在饱和土体上的振动问题进行了研究;Lu等[9]利用亥姆霍兹分解法推导了饱和半空间在移动点荷载作用下的动力响应的解析解;高广运等[10-11]基于Biot多孔饱和介质波动方程,推导了u-p格式和u-w格式的2.5维有限元方程,讨论了动力渗透系数、孔隙率、土骨架密度和剪切波速等参数对地面振动传播与衰减的影响规律。
当地下水位发生变化,土体性质也会随之发生改变[12-13]。地下水会使土体出现分层,导致振动波的反射和折射,会影响土体的固有频率,土体中的动力响应规律也会发生变化[14-15]。本文将地下水位以上的土层假设为弹性介质,通过Biot多孔介质方程的退化形式,来描述波在弹性介质中的运动;水位以下采用多孔饱和介质进行模拟,推导了弹性层与饱和半空间的传递矩阵,得到了上覆弹性层饱和半空间地表位移表达式。在波数内研究了不同水位下土体中波的组成,在空间域内分析了水位变化对于地面竖向位移的影响。
1 基本方程
多孔饱和介质物理方程如下
σij=λδijθ+2μεij-αδijp
(1)
p=-αMθ+Me
(2)
式中:ui,wi(i=1,2,3)分别为固体土骨架位移以及流体相对于固体土骨架的位移;p为孔隙水压力;σij,εij分别为土体总应力应变分量;δij为Kronecker函数;e,θ分别为单位体积内土骨架的体积应变和流体体积应变,e=divw,θ=divu;λ和μ为Lame常数;α和M为饱和孔隙介质压缩有关的Biot参数。
Biot饱和多孔介质方程相对位移形式为
μui,jj+(λ+α2M+μ)uj,ji+αMwj,ji=
(3)
(4)
式中:ρ,ρf分别为饱和土体和液体密度;ρ=(1-n)ρs+nρf,ρs为土骨架密度,n为孔隙率;m=a∞ρf/f,a∞为孔隙介质弯曲系数;b=η/k,为反应黏性耦合的系数,η,k分别为孔隙介质黏性系数孔隙介质的动力渗透系数;K(t)为与时间相关的黏性因子;位移上方的点为对时间的导数;符号“*”为两个变量的卷积。
对Biot控制方程进行求解,将方程从时域-空间域变换到频域-波数域,变换规则如下
(5)
(6)
式中:“^”为t到ω的傅里叶变换;“-”,“~”分别为x到ξ和y到η的傅里叶变换。
按式(5)的规则,对式(2)和式(4)进行变换,则可得到液体相对位移和孔隙水压力之间关系
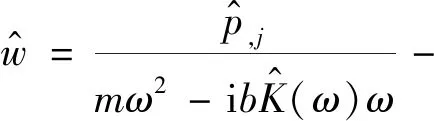
(7)
式中,ϑ=ρfω2/[mω2-ibK(ω)ω]
按式(5)的规则,对式(2)和式(3)进行变换,结合式(7)可得
(8)
对式(3)两边求散度可得
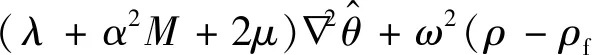
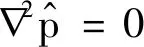
(9)
将式(8)代入式(9)可得
(10)
其中
β1=
按式(6),对式(10)进行傅里叶变换,求解可得
(11)
其中
式中,ιi(i=1,2)分别为饱和土体中的第一、二类膨胀波复波数,应满足Re(γj)>0(j=1,2)。通过式(11)可得
B2e-γ2z)-ϑ(A4eγ3z+B4e-γ3z)
(12)
B2e-γ2z)+iA3eγ3z+iB3e-γ3z
(13)
B2e-γ2z)+A4eγ3z+B4e-γ3z
(14)
η(A3eγ3z+B3e-γ3z)-γ3(A4eγ3z-B4e-γ3z)
(15)
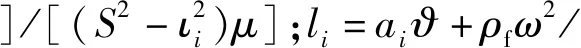
S为与饱和土体剪切波有关的复波数,满足Re(γ3)>0。Ai和Bi为与ξ,η,ω相关的任意函数,i=1,2,3,4。
将式(11)和式(13)~式(15)代入式(1)可得
B2e-γ2z)+γ3ημ(A3eγ3z-B3e-γ3z)-
(16)
(A2eγ2z-B2e-γ2z)+iγ3μ(A3eγ3z-B3e-γ3z)+
iημ(A4eγ3z+B4e-γ3z)
(17)
2μγ3(A4eγ3z-B4e-γ3z)
(18)
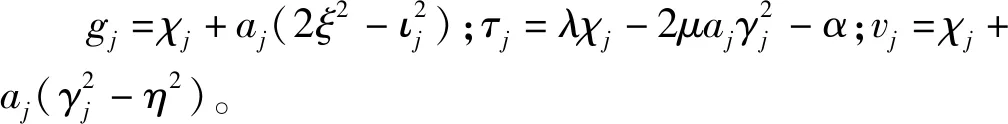
2 模型建立
地下水一般位于地表以下,可将土体模拟为上覆弹性层的饱和半空间模型,如图1所示。水位以上为干土层,材料属性假定为黏弹性地基土;地下水位之下部分为饱和半空间,模拟成多孔弹性材料。
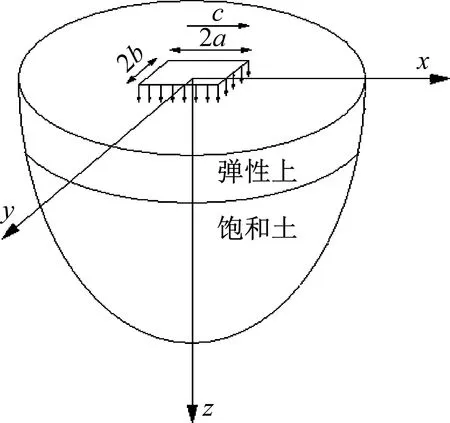
图1 上覆弹性层饱和半空间示意图
当地下水位上升时,淹没部分将达到饱和,视为多孔饱和介质;下层饱和土依旧采用Biot饱和介质方程进行模拟,上层弹性介质可以通过Biot方程采取特殊值退化进行描述。
图1中,地下水位于距离地表h处,在弹性土层表面处,有移动的简谐荷载作用,荷载尺寸为2a×2b,移动速度为c,圆频率为ω0,移动方向是由x负半轴向着正半轴运动。
为了计算不同土层的位移场和应力场通解,将式(18)写成矩阵的形式
(19)
式中:上标“i”为层数,从上到下编序,第二层为无限大半空间,“+”和“-”分别为指数项次数为正还是负。
每一层土体属性都是均匀的,并由一组材料参数定义。每个层都有一个局部笛卡尔坐标系统,原点位于其顶部,而Oxyz代表一个全局坐标系统,原点位于第一层的顶部表面。在局部坐标系中,顶面垂直位置zu(i)=0,弹性层底面垂直位置zd(1)=h。
其中:ui,σi,Ai和Bi(i=1,2)分量为
u=(ω,iξux,uy,uz)T,σ=(p,iξσxz,σyz,σzz)T,
A=[A1,A2,A3,A4]T,B=[B1,B2,B3,B4]T
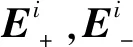
(20)
在两层交界处,上层位移场和应力场和下层位移场和应力场连续,用矩阵则可以表示为
(21)
根据无穷远处辐射条件,A2为零向量,而在第二层土层中位移和应力不为0,故B2不为0,可得
(22)
通过求解式(22)即可得到
A1=(T1)-1T2B1
(23)
其中
将式(23)代入式(20),可得
(24)
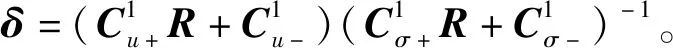
论文仅对地面竖向振动位移分量进行分析,因此,只考虑竖向荷载的作用,两种剪应力对地面的影响可以忽略,假设地基表面为透水边界,则存在以下边界条件
(25)
(26)
对式(26)进行式(5)和式(6)变换,可得
(27)
因此,地基表面的竖向位移则可表示为
(28)
φ44(ξ,η,0,ω)被称为饱和层状半空间在频率波数域的动力柔度矩阵,或称为频率波数域的动力格林函数矩阵。
通过式(20)和式(24)可以得到
(29)
利用式(28)即可计算出第一层土的下行波系数A1,通过传递矩阵就可以计算出整个层状饱和模型任意一点的位移、应力以及孔隙水压力表达式。
对式(28)进行逆傅里叶变换,从波数-频率域变换到时间-空间域,利用Dirac函数的性得模型任意一点位移
uz(x,y,0,t)=
(30)
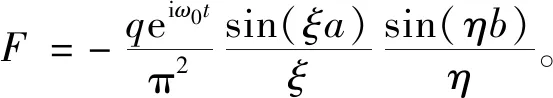
材料的阻尼采用常数的复数形式来表达:λ=λe(1+2iβ),μ=μe(1+2iβ),μe和λe分别为材料原本的Lame常数,β为土体的材料阻尼比。
根据式(30)可知,移动荷载的速度会对多孔介质响应的频率产生影响,当荷载速度过大时,会产生许多高频分量,而Biot方程主要应用于低频运动。
为了描述孔隙流体和固体骨架之间的高频阻力,将Biot理论与JKD模型[16]相结合,JKD模型可以近似处理低频与高频阻力相结合的问题。K(t)的频域表达式为
(31)
式中:ωc=bn/(ρfa∞),为将黏力控制的流动与惯性力主导的流动分离的过渡频率;ag为孔隙几何常数,多孔弹性介质通常取0.5。
3 计算结果分析
3.1 模型验证
当M,α,ρf,b,m接近于0时,可以采用饱和土半空间模型模拟波在单一弹性半空间中的运动,本文取所有参数为0.000 1,将h取足够小,上下层取同样的参数,可以模拟弹性半空间。选取与Jones等[17]一致的弹性土参数和荷载数值。
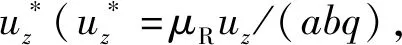
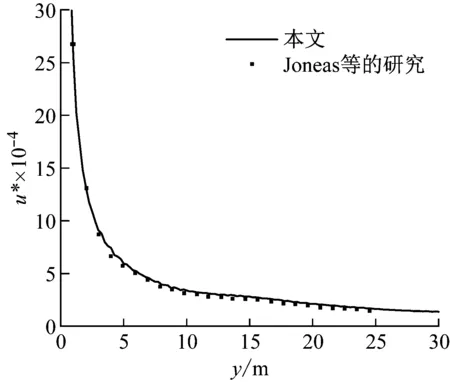
图2 本文计算结果与Jones等的结果比较
从图2中可以看出,本文计算结果与Jones等的计算结果基本相一致。
3.2 波数域内分析
为分析在移动简谐荷载作用下,水位变化对于地面位移响应的影响规律。
移动矩形荷载沿着x轴上运动,荷载的长宽为2a×2b=0.6 m×0.6 m,荷载集度为q=1/(a×b),荷载频率f为30 Hz,荷载速度c为100 m/s。
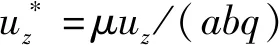
依据式(30)的计算结果,图3~图5分别为弹性半空间、以及上覆弹性层厚度为0.5 m,1.0 m和5.0 m下的波数域内位移幅值云图以及η=0处地表竖向位移实部的变化曲线。从图3~图5中可以看出:
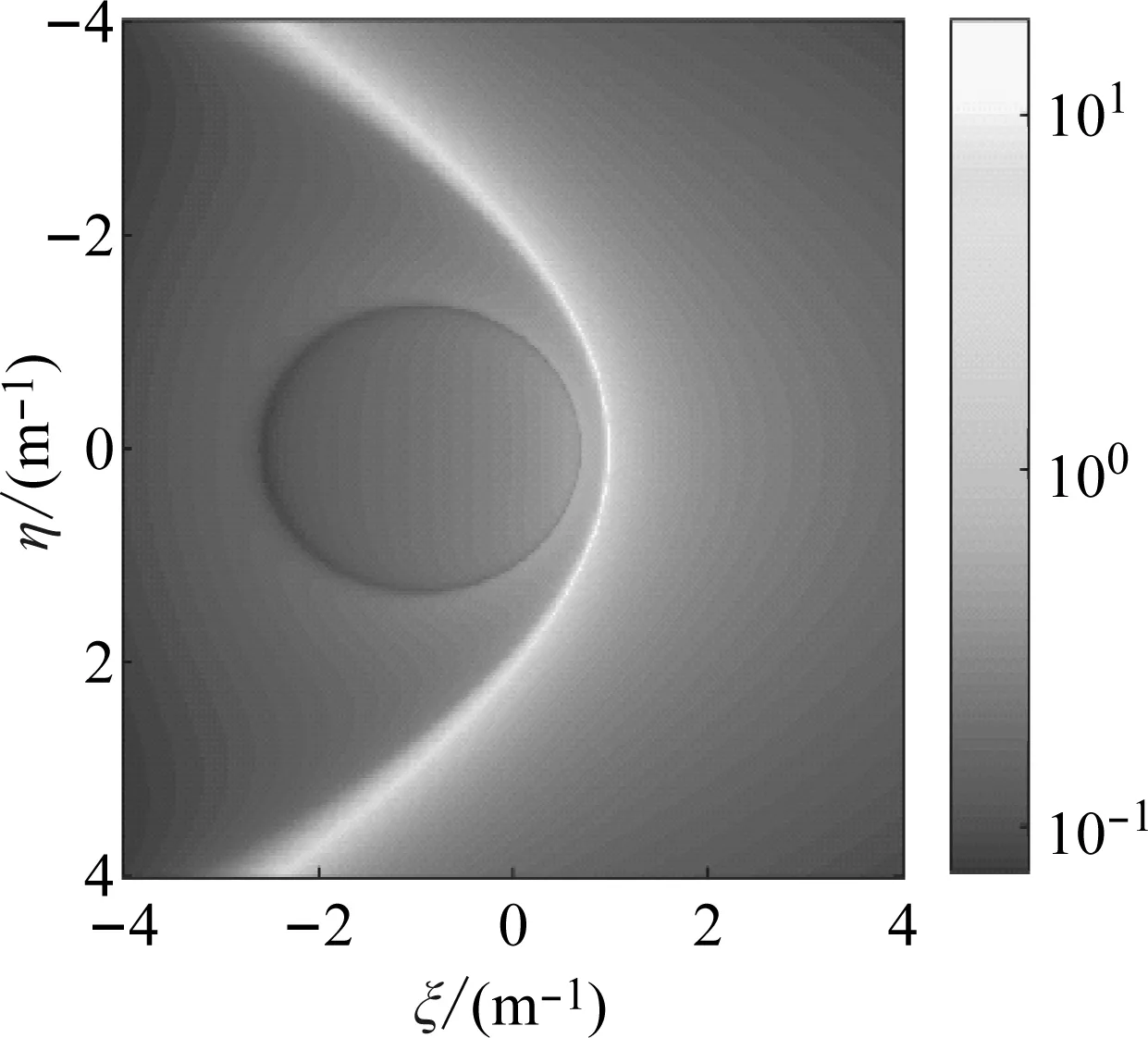
(a) 位移幅值云图
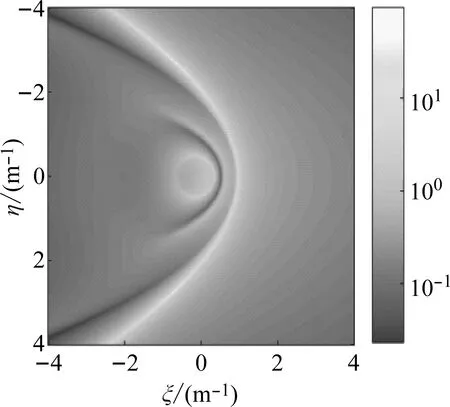
(a) 位移幅值云图
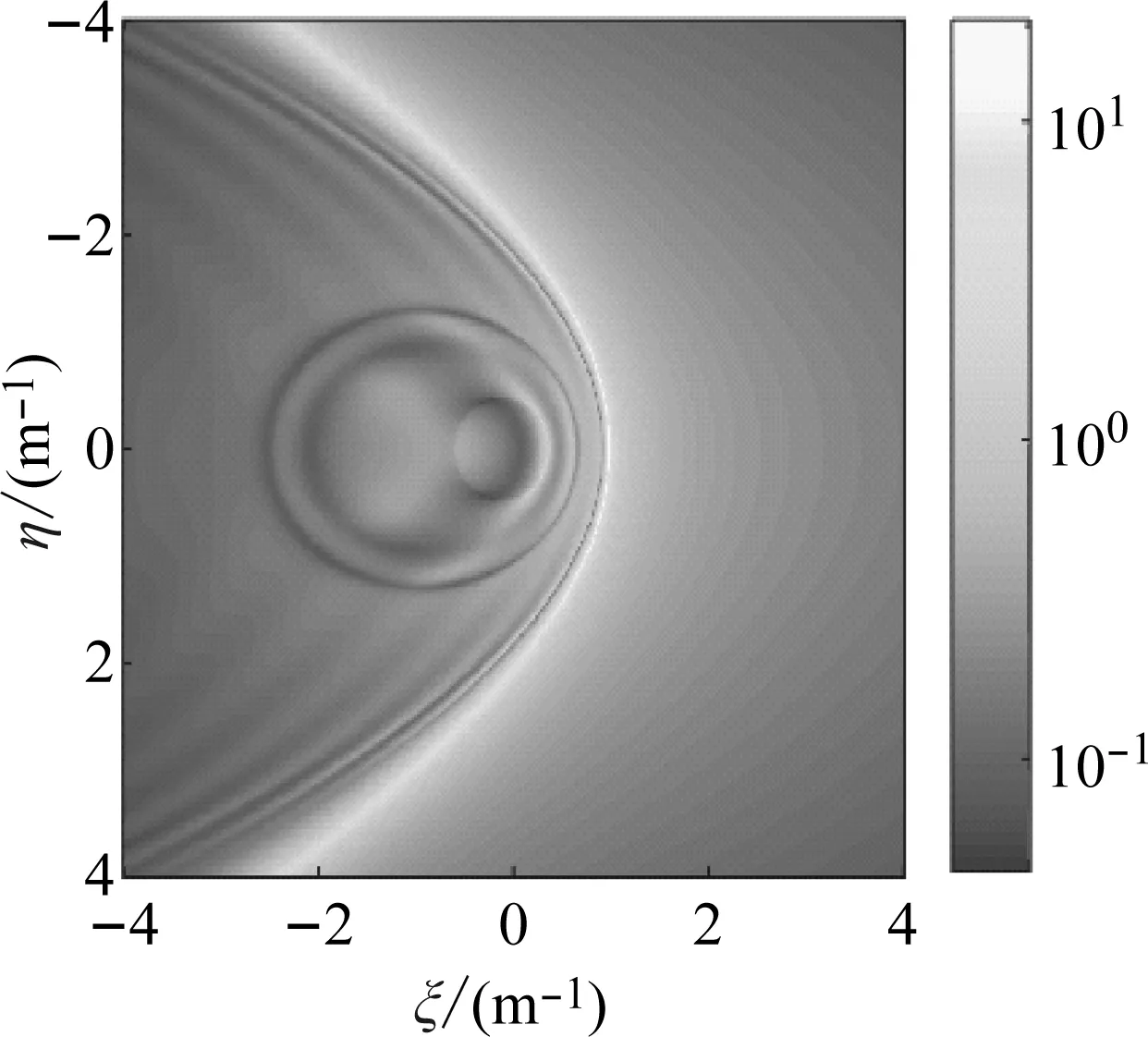
(a) 位移幅值云图
弹性半空间位移主要集中在3个正波数位置,分别代表R波、S波和P波,上覆弹性层饱和半空间中波的成分比起弹性半空间中复杂,这是因为P波和SV波在两种介质界面上会反射出多种类型的波,多种波对位移均产生影响。
当地下水位深度为1 m时,反射波对于地面振动的影响比较强,随着水位的降低,反射波的能量的越来越小;当水位深度为地下5 m时,反射波对地表振动的影响已经很小,波数分布基本和弹性半空间相同,地面振动响应主要还是由R波和S波决定。
3.3 空间域内分析
图6为不同地下水位下地表最大竖向位移幅值变化曲线。
从图6中可以看出:当地下水位距地表比较近时,地表的最大位移接近饱和半空间;随着水位的下降,位移开始减小,当水位深度达到0.3 m时,地表位移出现最小值;随着水位的不断降低,地表最大位移幅值呈不断增大趋势,水位深度超过4.0 m后,基本趋于稳定。
当水位比较高的时候,反射波对于地表动力响应影响比较大,但随着距离的增加,入射波迅速衰减,反射波的能量逐渐减小,且在传递到地面过程中,存在二次衰减,此时地基的动力响应类似于弹性半空间。
图7(a)是取水位深度为0.5 m,1.0 m,2.0 m和5.0 m时地表位移幅值随距离衰减的变化情况,图7(b)为图7(a)方框局部放大部分的曲线。
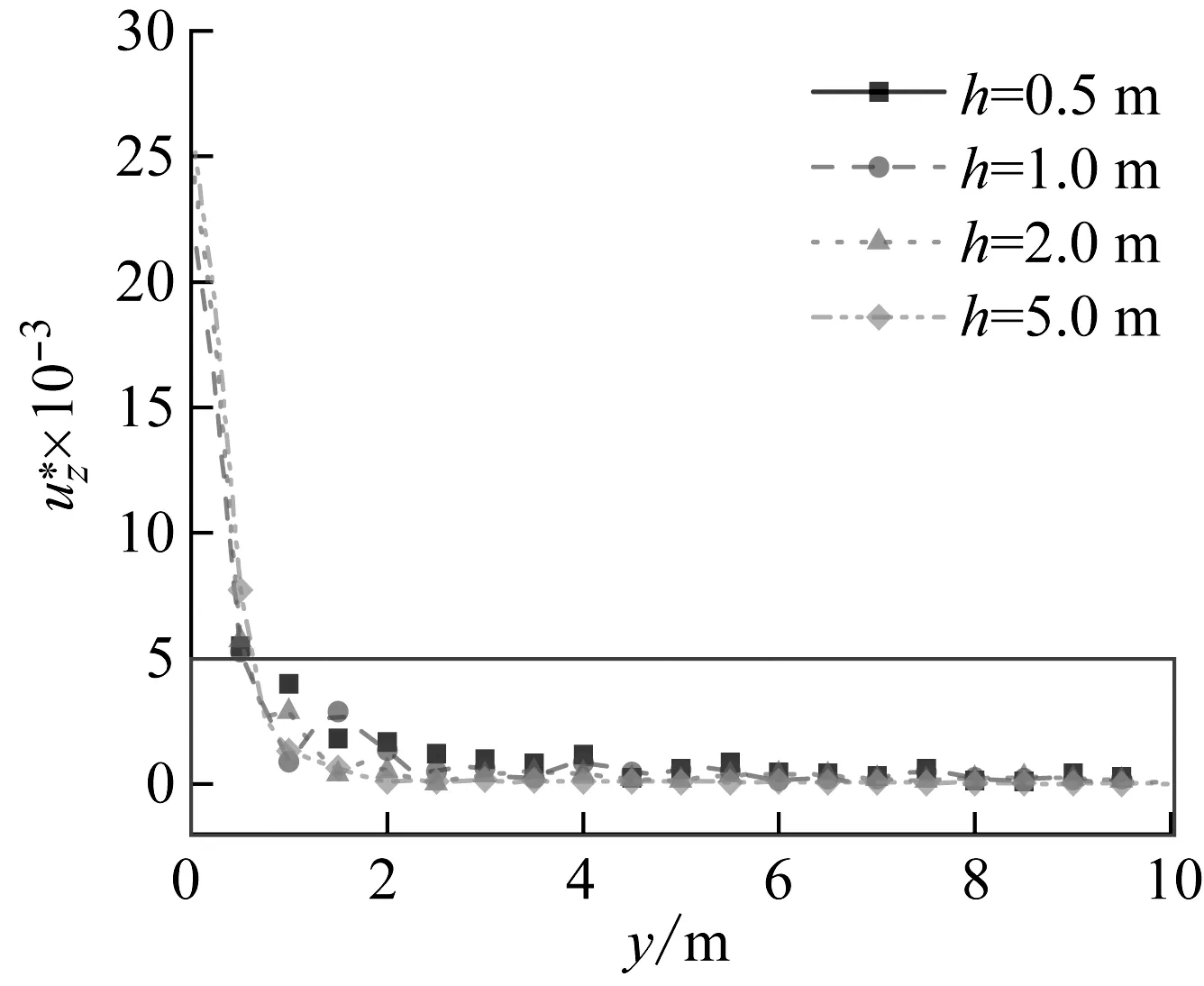
(a)
从图7中可以看出:当水位深度为0.5 m和1.0 m时,地表位移最大值却比2.0 m和5.0 m更小,位移幅值衰减更缓慢,衰减曲线起伏比较杂乱,原因是由于多种波振幅和波长不同,且存在一定的相位差,相互叠加之后导致的。
4 结 论
本文研究了移动荷载作用下,水位的变化对饱和土地基表面竖向位移的影响,得到了以下结论:
(1) 地下水位的存在会导致地基土分层,在分层界面上会产生反射波,对上覆弹性层动力响应产生一定影响。
(2) 当地下水位接近地表时,地表竖向位移接近饱和半空间;当水位下降,反射波对于地表竖向位移会产生一定影响,当水位下降到一定程度反射波影响减小,地表振动和弹性半空间中一样。
(3) 随着水位离地面距离越来越大,由于反射波的作用逐渐减小,会使得波的衰减起伏规律性变得减弱。

