双摆桥式起重机抗扰防摆跟踪控制
吴易鸣,孙 宁,杨钦朝,尹健宇
(1.东北大学 信息科学与工程学院,沈阳 110819;2.南开大学 人工智能学院 机器人与信息自动化研究所,天津 300350;3.南开大学深圳研究院 智能技术与机器人系统研究院,广东 深圳 518083)
起重机作为搬运、仓储、物流等各行业中都极为重要的重型装备之一,被广泛应用于工矿车间、仓库车站、集装箱码头、海洋开发等场合[1-3]。起重机具有欠驱动特性。此类具有欠驱动特性的系统在许多场合下可以节省驱动成本、精简机械结构、减小能源消耗。例如,机械臂[4]、飞行器[5]、移动机器人[6]、水下机器人[7-8]等。然而,由于缺失了控制输入,欠驱动系统相比于全驱动系统[9]在理论上更加难于分析。此外,对于起重机而言,另一个常见的特性为双摆效应。即货物与吊钩发生两级摆动。这种情况不仅更容易激发较大的货物摆幅,也更难于实现精准定位。
起重机系统的典型实现方法包括:输入整形与轨迹规划等开环控制方法[10],比例微分(proportional differential,PD)控制、先行二次规划(linear quadratic regulator,LQR)、滑模控制、鲁棒控制等闭环控制方法[11-15],其中,开环控制方法往往应用便捷,但较依赖于离线计算,对参数敏感。闭环控制方法提高了鲁棒性能但参数往往较多,实际效果受调参影响。
在理想条件下,较多研究将起重机吊运负载处理为单摆模型[16-23]。而在实际应用中,起重机系统往往通过绳索与吊钩的形式运输负载,使双摆效应较为常见。在这种情况下,起重机系统的控制输入数目不变,但欠驱动自由度增加,若将其简化为单摆结构并直接应用未考虑双摆效应的防摆方法将难以达到预期的防摆效果。截至目前,受到单摆起重机控制技术的启发,已有研究对典型的开环与闭环控制方法进行了改进。首先,是开环的指令整形技术[24-25]与轨迹规划技术[26-27]。然而,起重机往往应用于复杂工况,易受到外部扰动的影响。在这种情况下,Wu等[28]利用滑模控制技术实现了分布式负载的防摆吊运。石怀涛等[29]引入摆角耦合项实现了两级摆动的加速抑制。Qian等[30]则利用了模糊控制技术实现了防摆吊运。
在实际应用中,可结合开环轨迹规划与闭环轨迹跟踪控制实现负载吊运。然而,开环方法大多着眼于轨迹的离线规划环节;闭环控制方法大多为定位控制,跟踪控制较少。为进一步提升双摆起重机系统在轨迹跟踪环节的抗扰性能,提出了一种抗扰防摆跟踪控制方法。该方法的贡献归纳如下:① 引入集总干扰项,并结合状态观测器设计更新律在线估计扰动,从而使系统能够处理未建模动态、外部扰动等未知不确定性;② 设计虚拟控制器,使系统能够实现对既定轨迹的鲁棒跟踪,且通过严格的理论分析证明了跟踪误差的有界性;③ 在更新律中引入一个可调节的更新因子,并从理论上证明了更新因子增大跟踪误差减小,实现对跟踪误差的约束。从问题解决方面来看,该方法能够提高系统对建模误差、未建模动态、不确定性等因素的鲁棒性,同时可在理论上约束跟踪误差实现良好的轨迹跟踪。从理论创新方面来看,该方法受到L1自适应控制的启发,在此框架下进一步探索了如何处理具有较多欠驱动自由度的系统的抗扰控制问题。
1 问题描述与模型变换
首先,给出双摆桥式起重机系统的动力学方程如下
(1)
(mh+mc)gl1sinθ1=0
(2)
(3)
其中,各变量与已知参数的定义如表1所示。本文的控制目标是台车位移跟踪给定轨迹xf(t),并最终稳定在期望的目标值xd。同时,在跟踪控制的过程中实现两级摆动的有效抑制。
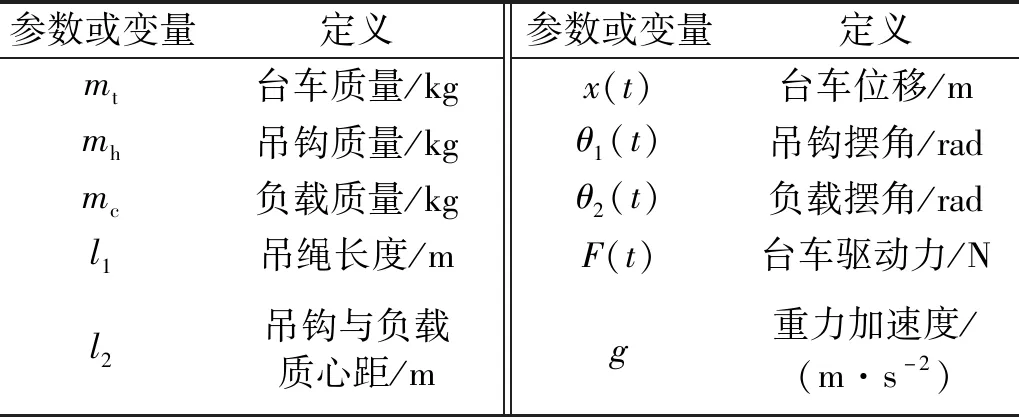
表1 系统参数与变量定义
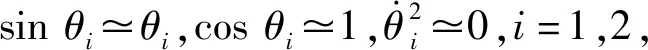
(4)
(5)
(6)
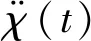
(7)
同时,用式(6)减去式(5),可得
(8)
基于式(7)、式(8)与χ(t)的定义,可知原始状态变量x(t),θ1(t),θ2(t)均可以用新的状态变量χ(t)来表示。于是,可将式(4)改写为如下形式
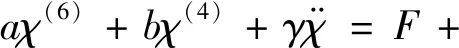
(9)
式中:参数a=mtmhl1l2[(mh+mc)g2];参数b=[mt(l1+l2)+mhl2]g;参数γ=mt+mh+mc;为未知的建模误差。后续的控制律设计与稳定性分析将基于变换后的模型式(9)。等效地,基于新的状态变量与动力学模型式(9),控制目标变为使χ(t)跟踪轨迹xd(t)。
2 控制设计及稳定性分析
为实现控制目标。接下来将对控制输入F(t)进行设计。给出控制系统的整体流程框图如图1所示。
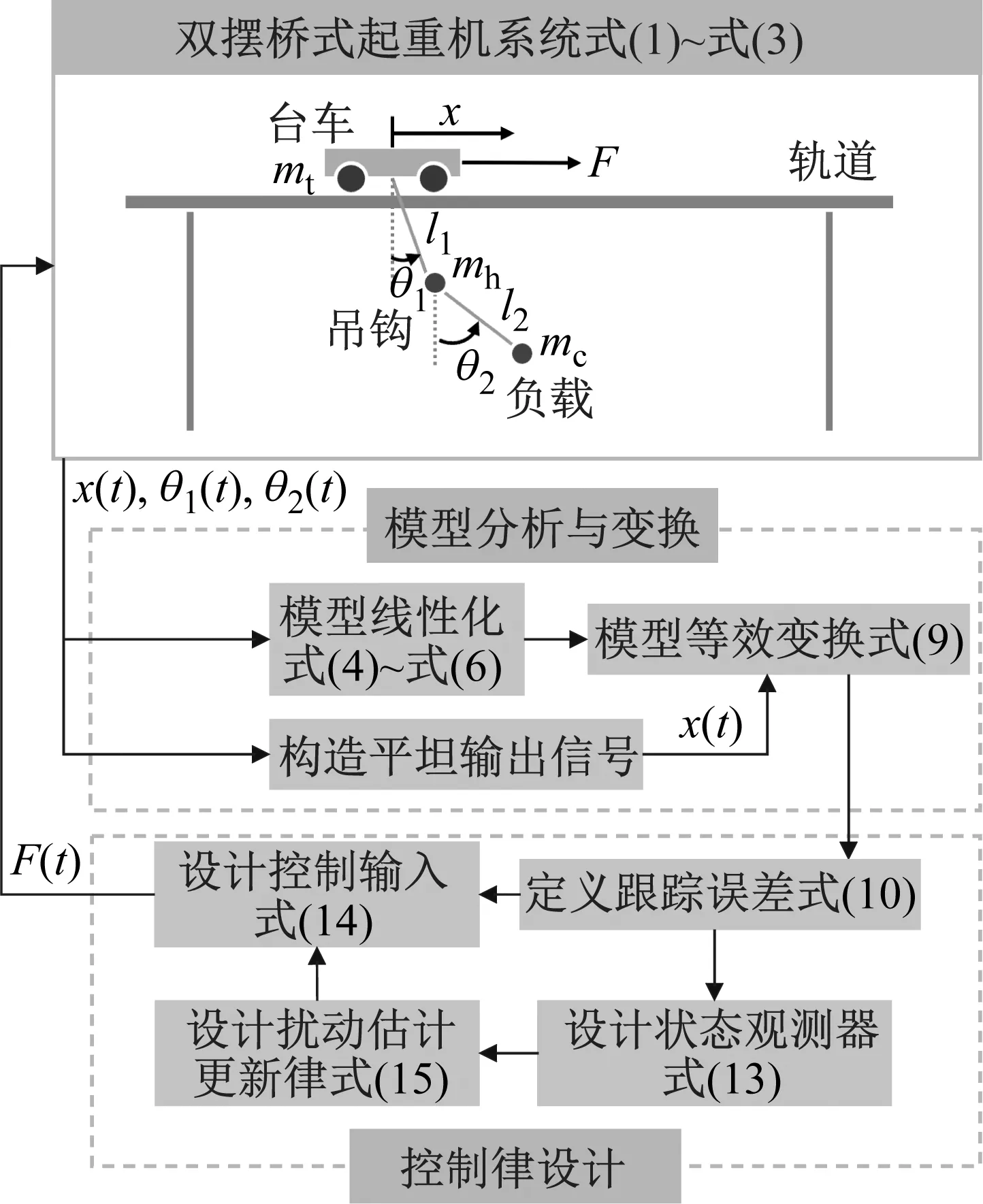
图1 控制系统流程框图
首先,定义如下误差变量eχ(t)∈R及其导数
(10)
式中,i=1,2,3,…,6。结合后续的分析,最终的控制输入的形式设计如下
(11)
(12)
其中,Aχ∈R4×4,Bχ,Cχ∈R2分别定义如下
(13)
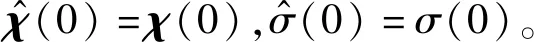
(14)
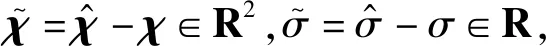
(15)
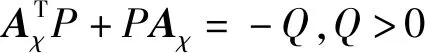
基于所设计的控制器与更新律,为方便后续分析,给出闭环系统方程如下
(16)
并根据实际应用情况给出如下假设:
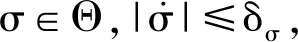
接下来,将通过分析论证如下的定理,以证明闭环系统的稳定性。
定理1对于双摆桥式起重机系统式(9)与式(12),所设计的控制器与参数更新律式(11)、式(14)与式(15)能够使如下结论成立。
(1) 当未知扰动是时变量时,所有的系统状态有界,并满足
(17)
(18)
(19)
式中,存在h∈R2×2,使hT(Is-A)-1Bχ=N1(s)/N2(s),deg(N1)-deg(N2)=1成立。
证明对定理1展开证明需对如下两种情况进行讨论与分析:
情况1考虑未知扰动时变的情况。首先,构造如下标量函数V(t)
(20)
并求导,可得
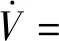
(21)
(22)
V≤σmΓ-1⟹V∈L∞
(23)
并可通过式(13)、式(14)与式(23)推知
(24)
即可得跟踪误差有界。
为进一步证明定理1,可将式(21)与式(23)中的结论进行整理,并得到
(25)
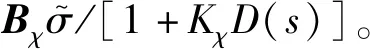
(26)
接着,若将式(12)与式(13)相减,可得到
(27)
则式(26)中的不等式变为
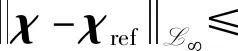
(28)
即式(18)成立。此外,利用式(27),还可从式(14)与式(16)得知
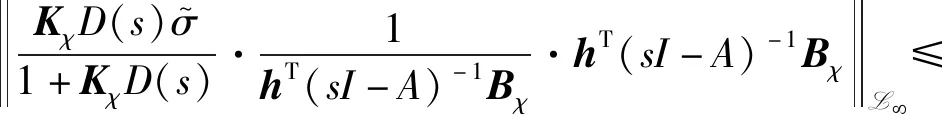
(29)
即式(19)成立,情况1得证。值得注意的是,在式(17)~式(19)中,随着参数Γ的增大,跟踪误差减小,而当Γ趋于无穷大时,跟踪误差趋于0。表明在应用时,可通过增大Γ的值来减小跟踪误差,使其满足需求。
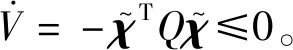
即情况2得证。
因此,综合结论式(25)、式(28)、式(29)与式(30),定理1证毕。
3 仿真与试验结果分析
本章将对所提方法进行仿真与试验验证。仿真模型使用原始模型式(1)~式(3)。试验时应用图2所示的桥式起重机系统样机[35]。在此给出所提控制律与更新律参数的调节规律。kp,kd类似PD控制中的P增益与D增益;Kχ为滤波相关的参数;更新因子Γ越大,跟踪误差的界越小。

图2 双摆桥式起重机硬件试验平台
3.1 仿真验证
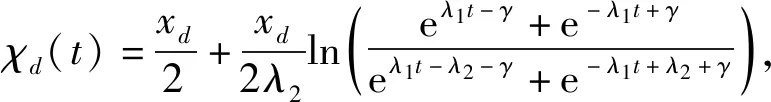
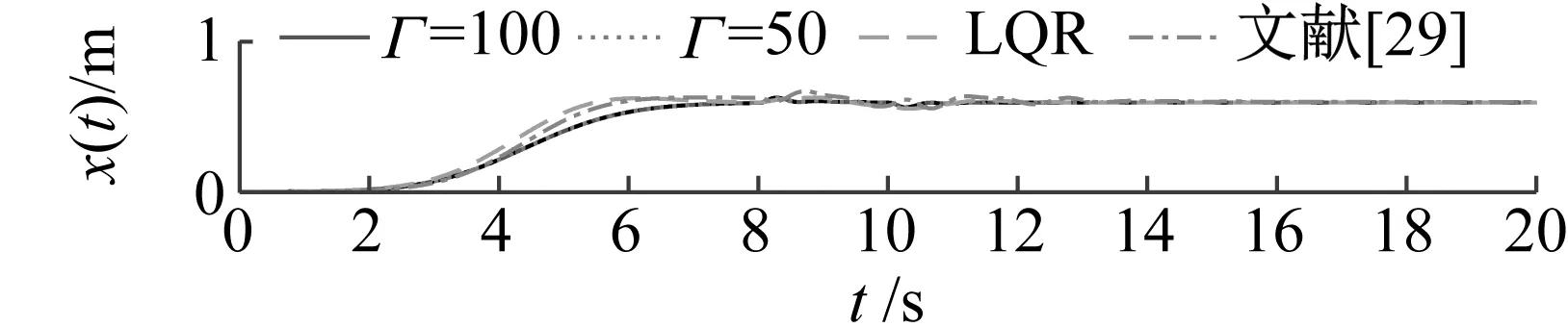
仿真时选取了两种对比方法,分别为:经典的LQR方法与石怀涛研究中的方法。LQR控制器的控制增益为k1=60,k2=49.33,k3=-128.72,k4=-7.49,k5=20.4,k6=-6.84。石怀涛研究中控制器的控制增益为kp=5,kd=20。同时,在仿真中加入外部扰动,对比各方法的跟踪与防摆效果。仿真结果如图3所示,其中,为验证理论结果,在仿真时给更新因子Γ赋不同的值。从图3中可以看出:① 所提方法引入集总干扰项,能够在线补偿未知不确定性,较快速地消除了扰动的影响;② 所提方法可良好跟踪时变轨迹,并可使吊钩与负载额的摆幅在2 deg以内;③ 根据仿真数据,当分别取Γ=100,Γ=50时,位移的跟踪误差分别稳定在0.003 m与0.007 m,即验证了Γ越大跟踪误差越小的理论结果。综上,仿真结果验证了所提方法的有效性。
(a)
3.2 试验验证
试验1跟踪S型轨迹。令轨迹参数为xd=0.5 m,λ1=1.1,λ2=0.1,γ=3.5,增益为kp=167,kd=9,Kχ=10,并取Γ=5。试验结果图4所示。可以看出,所提方法能够实现对给定轨迹的良好跟踪,且在跟踪过程中有效地抑制吊钩与负载的两级摆动。

(a)
试验2施加外部扰动。本组试验为验证所提方法针对外部扰动的鲁棒性,其试验结果如图5所示。在5~15 s加入扰动,可以看出在加入了外部扰动的情况下,所提方法依然能够很好地跟踪期望轨迹,有效地抑制人为施加在欠驱动摆角上的干扰。
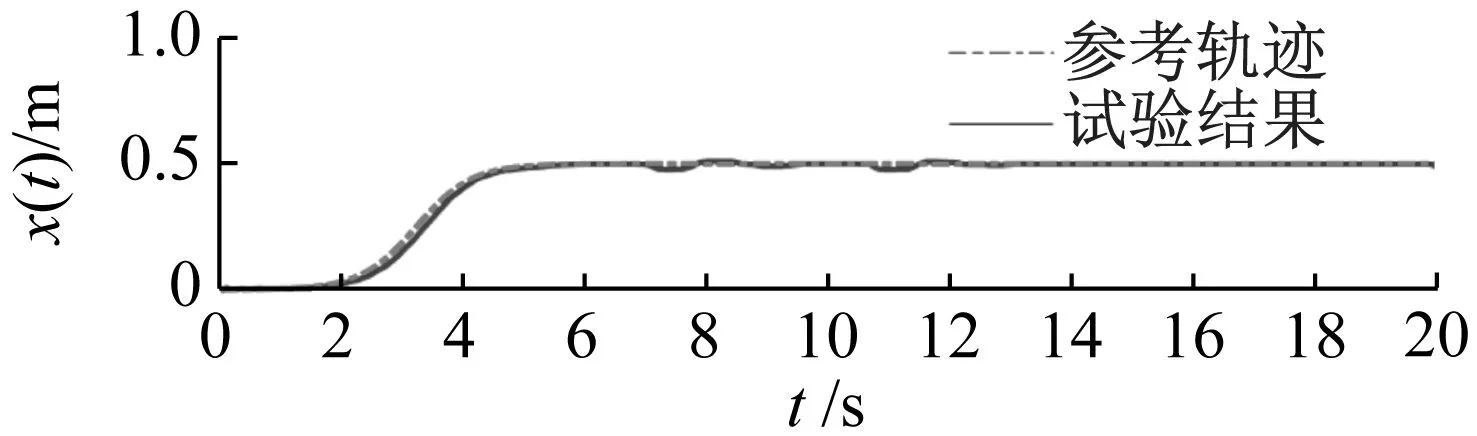
(a)
4 结 论
针对存在未知不确定性与未建模动态的情况,基于L1自适应控制技术提出了一种双摆桥式起重机系统抗扰防摆跟踪控制方法,实现了对S型轨迹的鲁棒跟踪。具体而言,首先分析模型,引入集总干扰项处理未建模动态。之后,引入虚拟控制量并设计状态观测器、滤波环节以及未知扰动更新律。经过严格的理论分析证明了跟踪误差均有界,且更新因子越大跟踪误差越小。试验结果表明所提方法具有良好的跟踪性能,且能够快速消除负载摆动。

