转化思维：小学数学解题的“突破口”

冒文峰

摘 要： 学科素养下，小学数学教学不再是培养解题“工具人”，而是在学习中形成一种思维能力，使得学生在学习中学会转化，能够灵活运用各种数学知识点，解决常见的问题，不断提升小学生的数学解题能力.本论文就以此作为研究视角，结合针对性的例题，针对转化思维在小学数学解题中的具体应用进行了详细地探究，具备一定的参考价值.

关键词： 小学数学；解题教学；转化思维；突破口

小学生在解答数学问题的时候，常常会遇到一些“拦路虎”，如：复杂的运算、不规则的图形、没有明确解题思路等，如果一味地按照传统的思路和方法解题，就会导致解题过程繁琐，且频频出现解题错误，甚至凭借已有的知识和能力根本无法找到具体的解题思路等.面对这一现状，为了帮助学生顺利突破难题，提升数学解题能力，本文将引导学生学会转化，科学运用转化思维，寻找新的解题思路.

1 转化思维在小学数学解题中的实践

在小学数学解题中，转化思维是一种非常重要的数学思维，即：将一个问题进行转化，使其成为另一个问题，旨在通过转化这一过程，解决数学问题.鉴于小学数学学科的特点，转化思维包含的内容比较多，可结合不同的题目类型，灵活运用各种转化方式.

1.1 化繁为简

鉴于数学学科的特点，计算教学贯穿整个小学阶段，占据十分重要的地位.在培养小学生数学运算能力时，常常会遇到一些极为复杂的题目，如果按照常规的四则混合運算顺序，常常面临着复杂的运算过程，并且小学生还会在运算过程中出现各种各样的错误.鉴于此，就可充分借助转化思维，对其进行重新组合，使其变得更加简单.

例1   计算

（1 000+998+996+…+906+904+902）-（2+4+6+……96+98+100）.

解析：  在这一问题中，如果单纯地按照常规的混合运算顺序，就要按照“先括号”的原则，之后并按照先乘除后加减的顺序进行.但如果按照这种方式进行计算，将会面临着极大的运算量，并且计算过程十分复杂，稍不留神就会出现各种各样的错误.鉴于此，在开展解题教学时，就可指导学生基于转化思维，对上述的算式进行观察，找出其中存在的规律：1 000-100，998-98，996-96……，902-2结果都相等.因此，可将上述的算式进行打破、重组，转化成为一个新的算式：

（1 000-100）+（998-98）+（996-96）+…+（906-6）+（904-4）+（902-2）.

如此，学生即可迅速得出正确的答案.可见，在这一题目解答中，关键点就在于“转化”，将带有括号的四则混合运算进行转化，使其成为相等差值的减法运算.

1.2 化数字为图形

在当前小学数学课堂教学中，部分教师受到传统教学理念的制约，常常人为地隔离代数和几何内容.但针对数学学科来说，数和形原本就相辅相成，属于一个有机统一体中.经过大量的解题教学实践证明，将数学信息转化为图形信息，能够帮助学生迅速形成明确的数量关系，找到问题的解答“突破口”.

例2   已知A，B两地距离为16  km ，小明和小红分别从同一个地方出发，以相同的速度，朝着相同的方向出发.小明先出发，小红过一段时间之后再出发，当小红出发3个小时之后，两个人的距离为80  km ，此时小红行走的路程是小明的 3 5 ，请问小明比小红早走几个小时？

解析：  这是一道常见的分数应用题，如果按照常规的方式进行解题，学生在审题的过程中，常常难以厘清题目中的数量关系，导致其出现解题错误.鉴于此，就可指导学生借助转化思维，将上述题目进行转化，即：假如两个人同时从A地出发，前往B地，小明先出发一段时间，小红出发3个小时之后，她行走的路成为小明的 3 5 ，那么小明比小红早出发多久？

通过第一步转化之后，题目就变得更加清晰了；接着，再次进行转化，使其成为形象的图形（如图1所示）.如此，学生结合线段图设，就能结合题目中的已知关系，利用分数式得出：3÷ 3 5 -3=2（小时），高效完成了这一题目的解答任务［1］.

例3   计算 1 2 + 1 4 + 1 8 + 1 16 .

解析：  在对这一分数加法计算中，如果按照常规的思路，学生需要先进行通分，并进行计算.但这一过程存在一定的难度，并且极容易计算错误.面对这一现状，在指导学生解题时，就可借助“转化”思维，将分数计算题目转化为图形涂色问题（如图2所示），使得学生在图形涂色中，顺利作出正确答案，即 15 16 .

1.3 化不规则为规则

在小学数学解题中，常常会遇到一些求不规则的图形面积的题目，如果按照常规的解题思路进行解答，常常面临诸多困难，难以完成其解答.鉴于此，就可借助转化思维，将原本不规则的图形进行转化，使其成为规则图形的和、差等，进而顺利完成其解答.

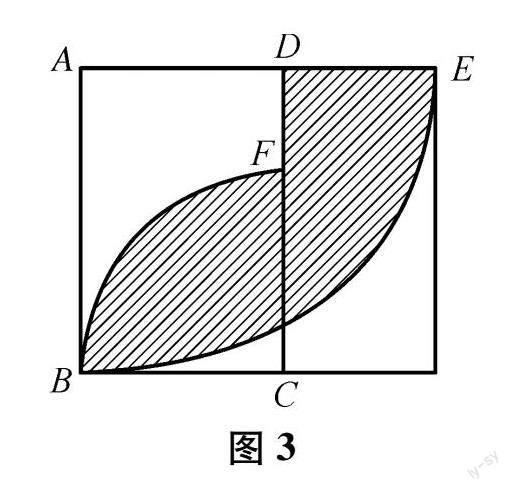
例4   如图3所示，已知长方形ABCD，AB长6厘米，BC长4厘米，扇形ABE的半径AE为6厘米，扇形BCF的半径CF为4厘米，求：阴影部分的面积.

解析：  在这一题目中，阴影部分是一个不规则的图形，学生无法借助面积公式进行直接求解.鉴于此，唯有借助转化思维，将阴影部分面积转化为几个规则面积的和（差）.经过图形分析，可发现这一组合图形中一共包含了三个规则图形，长方形、大扇形、小扇形，并且这三个规则图形的面积是可以求出来的.接着，对组合图形进行分析，发现阴影部分面积就是大扇形面积-空白ABFD面积.而空白ABFD面积恰恰是长方形ABCD面积-小扇形面积.由此，就借助转化思维，得出S 阴影=S 大扇形-（S 长方形-S 小扇形）

因为S 大扇形=6×6× π ÷4=9 π ，S 小扇形=4×4× π ÷4=4 π ，S 长方形=6×4=24，

所以，S 阴影=S 大扇形-（S 长方形-S 小扇形）=9 π -（24-4 π ）=13 π -24=16.82（平方厘米）.由此可见，在本题目中，解题的关键就是“转化”，将原本不规则图形转化为规则图形的面积差，进而轻松解决这一问题［2］.

1.4 化难为易

在小学数学应用题中，常常会遇到一些难度系数比较高的题目，如果按照常规的思路进行解题，不仅找不到“突破口”，甚至还会受到题目条件的干扰，产生错误的解题思路.鉴于此，必须要借助一定的转化思维，将原本复杂、难度系数比较高的题目进行转化，使其成为学生便于理解的题目进行解答.

例5   甲乙在400米的跑道上，甲以每秒钟6米的速度跑步，乙以每秒4米的速度跑步，二人同时从同一起跑线上起跑，如果沿着相反的方向跑步，二人从起跑到第三次相遇需要多少的时间？

解析：  这是一道典型的“相遇”问题，是小学数学常考的题目.在这一题目中，已知跑道400米，甲乙二人速度，以及跑步在反方向下的相对速度，以及二人同时同一点起跑；二人从起跑到第三次相遇时间相等；未知量是二人第三次相遇的时间.在对这一题目进行解答时，如果按照常规的思路进行解题，常常面临着过程复杂、思路不清的现象，难以找到解题的突破点. 鉴于此，在进行解题的时候，就应带领学生借助“转化”的方式，将二人在跑道上相遇一次视为一圈，那么题目中两人相遇的三次，即跑了三圈，总长度為400×3=1 200（米）.如此，结合题目中已知条件得知，两人反方向的相对速度是6+4=10米/秒， 即相遇三次的时间为400×3÷（4+6）=120（秒）.可见，在本题目中，解答的关键就是“转化”，将相遇三次转化为总长度，之后即可简单解答这一问题.

1.5 化隐含为明显

在小学数学解题中，常常会遇到一些隐含的条件，这些条件没有明确给出，需要学生在解题的时候，通过分析深挖出来，才能在隐含条件的辅助下，顺利解决相关问题.但具体解题时，这些隐含条件常常不易被发掘，需要借助一定的转化思维，方可将其挖掘出来.

例6   有三筐水果，甲乙两筐水果共重20  kg ，乙丙两筐水果共重18  kg ，甲丙两筐水果重12  kg ，求甲乙丙三筐水果共重多少？

解析：  学生在解答这一问题时，初次解读之后，常常感觉无从下手.因为在题目中，已知条件分别是甲乙、乙丙、甲丙的重量；未知量则是甲乙丙三筐水果的重量分别是多少.在这一情况下，如果按照常规的思路进行解题，就会发现根本无法套用已有的公式解答问题.鉴于此，必须要借助转化思维，将甲乙、乙丙中共同含有的乙筐水果重量进行转化，使其成为显性的条件，本题即可变得明朗起来：已知甲乙两筐水果共重20  kg ，乙丙两筐水果共重18  kg ，那么甲筐水果比丙筐水果重20-18=2（ kg ）；又因为甲丙两筐水果重12  kg .因此，甲筐中水果的重量为（12+2）÷2=7（ kg ）；丙筐水果重量为12-7=5（ kg ），乙筐水果重量为20-7=13（ kg ）.可见，在本题目解答中，核心突破点在“从‘隐含条件到‘显性条件的转化”，充分借助转化思维，对题目进行分析，从中挖掘出隐含的条件，并以此作为切入点进行解答［3］.

1.6 化特殊为一般

在小学数学解题中，常常存在一定的规律，学生在解答问题时，唯有掌握了其中蕴含的规律，才能找到具体的解题方法.而要达到这一目标，在日常解题教学中，就必须要引导学生借助转化思想，将特殊的数学问题进行转化，使其成为一般性的问题，进而运用一般的规律解答问题.

例7   一条直线上有n个点，请问这条直线上有多少条线段？

解析：  学生在解答这一问题时，常常疑问题目中没有给出具体的数字，导致学生不知道如何下手，难以形成具体的解题思路.鉴于此，教师在开展教学时，就可借助转化思维，通过举例子的方法，引导学生思考：如果这一条直线上只有1个点，那么就没有线段；如果线段上有2个点，则存在一条线段；如果有3个点，则存在2条线段；如果直线上有4个点，则存在3条线段.接着，引导学生以此类推，如果有n个点，那么则存在n-1条线段.之后，再次指导学生进行画图验证.可以说，在这一问题的解答中，就是借助了转化思维，将没有数字的特殊题目进行转化，使其成为具体的数字关系题目，便于学生在列举中，总结出其中蕴含的规律，进而找到题目解答的方法.

1.7 化单一解法到多种解法

在小学数学解题中，学生常常会遇到一些复合型的问题，而这些复合型的问题常常存在多种解法.又是面对新课程改革下的要求，教师在开展解题教学时，不要仅仅局限于学生解题的结果，还应关注学生在解题过程中的思维发展情况，旨在借助解题教学，帮助学生打破思维的束缚，使其在多角度思考和解题中，促进数学思维能力的发展.鉴于此，数学教师在日常解题教学中，唯有坚持转化思维，促进单一解答方法到多种解法的转变.

例8   已知一根钢管长2.7米，截下全长的 3 10 ，做了9个零件，剩下的还可以做多少个零件？

解析：  这一题目难度系数比较小，学生在解答的时候，可从不同的角度进行思考，并计算出正确的答案.鉴于此，在培养小学生数学思维能力时，就应立足于转化思想的内涵，引导学生对题目内容进行转化，并从不同的角度进行解答：① 将其转化成为工程问题，将整个管长视为单位“1”，则可得出解题方案： 1- 3 10  ÷  3 10 ÷9 =21；② 将其转变成为倍比法，结合题目中已知条件，得出已经做了3份，还余下7份未加工成零件，余下的份数是已做份数的7÷3= 7 3 倍，结合 3 10 做了9个零件，由此得出余下的还可以做7÷3×9=21；③ 将其转化为归一法，即3份做9个，即1份做3个零件；还余下7份，即可得出9÷3×7=21；④ 将其转化为分数对应关系式，即9个零件占据全长（单位“1”）的 3 10 ，即可结合这一对关系，得出这根钢管剩余的还可以做9÷ 3 10 -9=21.由此可见，在这一题目中，通过转化思维的应用，从不同的角度，利用不同的思维和数学知识进行了解答，使得学生在转化、解答的过程中，逐渐形成了极强的数学思维，真正满足了小学数学学科素养下的教学目标［4］.

2 基于小学数学转化思维解题教学启示

经过课堂教学实践得知，将转化思维应用到小学数学课堂教学中，彰显出显著的应用价值，显著提升了小学生的数学解题能力，使其在转化思维的辅助下，迅速攻克难题，并在解题分析中，实现了数学思维的发展.鉴于此，作为一名优秀的小学数学教师，必须要转变传统的数学解题教学模式，遵循“熟练、简明、典型”的原则，将其科学、合理地融入到解题教学中.

首先，从熟练性原则上来说，要求教师在引导学生转化题目时，应坚持从“陌生到熟悉”“从复杂到简单”的原则，力求通过转化，使得原本复杂、陌生的数学问题变得更加简单、熟悉，学生可运用已有的知识和方法进行解答；

其次，从简明性原则上来说，在引导学生进行转化时，可通过拆解条件、分析题目的方式，将原本复杂的数学问题转化成为简单的问题.而在这一过程中，必须要带领学生对题目进行深入分析，基于不同条件之间的联系进行转化.

最后，从典型性原则上来说，在借助解题教学训练学生转化思维时，必须要选择具备典型性、代表性的数学题目，以便于学生在典型的训练中，真正掌握这一数学思想和方法，是在日后遇到同类型题目时，可迅速进行解答［5］.

3 结束语

综上所述，转化思维作为小学数学解题中常用的一种思维模式，不仅能够促进学生对数学知识的理解，还能强化小学生的数学学习兴趣，使其在转化思维的引导下，促进复杂问题、难题、特殊问题的转化，以便于学生运用所学的知识，轻松进行解答.同时，小学数学转化的过程，也是学生思维发展的过程，小学生也在转化中促进了思维的发展，真正提升了小学生的数学综合素养.

参考文献：

［1］ 吴云泽.小学数学解题中转化思维的有效应用分析［J］.数学学习与研究，2022（18）：93 95.

［2］ 薛祖佳.转化思想在小学数学解题中的妙用［J］.数学大世界（上旬），2022（6）：62 64.

［3］ 徐建干.转化思维在小学数学解题中的有效应用［J］.数学教学通讯，2022（13）：69 70.

［4］ 劉俊彬.转化思维：小学数学解题教学的突破口［J］.基础教育论坛，2022（12）：82 83.

［5］ 雷维维.转化策略在小学数学解题教学中的应用分析［J］.数学学习与研究，2021（28）：58 59.