地铁-公交加权复合网络关键站点识别及鲁棒性研究

郑乐，高良鹏，陈学武，宋波，丁磊

(1.南京邮电大学，现代邮政学院，南京 210003；2.福建工程学院，交通运输学院，福州 350118；3.东南大学，交通学院，南京 211189；4.南京邮电大学，碳中和先进技术研究院，南京 210023)

0 引言

为弥补传统常规公交容量与速度方面的不足，国内各大城市都在加快以地铁为主的城市轨道交通的规划和建设。截至2022 年末，中国内地开通城市轨道交通的城市已有55 个，运营里程已超过1 万km[1]。部分大城市的地铁已实现网络化运营，形成以轨道交通为骨干和地面公交为主体的多模式公共交通体系[2]。地铁网络与公交网络相融合所形成的复合网络在功能上相辅相成，极大地方便了城市居民的出行，提升了城市公共交通的整体服务水平。然而，随着地铁-公交复合网络规模的逐步扩大，交互逐渐增加，对其网络鲁棒性也提出了更高的要求。尤其是关键站点失效会极大影响复合网络的运输效率，甚至引发级联失效[3]。因此，识别复合网络中的关键站点并分析其对网络鲁棒性的影响，不仅仅对指导线网规划具有重要意义，还可以为突发公共事件下的应急保障预案提供决策支持。

目前，国内外学者主要采用复杂网络理论研究地铁-公交复合网络，主要研究内容包括复合网络的网络特性分析、复合网络的鲁棒性分析以及复合网络的关键站点识别。在复合网络的网络特性分析方面：罗艺等[4]采用Space L 和Space P 方法分别构建公交-地铁复合网络及其子网络，实证分析北京地铁-公交复合网络的度分布、平均路径长度及聚类系数等网络拓扑特征，并证明了复合网络的小世界特性和无标度特性；WANG 等[5]构建公交-地铁复合超网络模型，并以西安为例，分析超网络的网络特征，结果表明，复合网络相比于单一网络更加高效，能够更加充分地发挥地铁与公交的各自优势，提升公共交通系统的整体效率；潘恒彦等[6]综合考虑车辆发车间隔、载客能力以及区间车速，建立地铁-公交加权复合网络，并对比无权及加权网络的网络特性。在复合网络的鲁棒性分析方面：沈犁等[7]等以成都为例，研究地铁-公交复合网络的鲁棒性，结果表明，相比单一子网络，复合网络具有更好的抗毁性；张琳等[8]提出一种耦合站点失效判别的规则，并采用蓄意攻击以及随机攻击两种方式分析复合网络的静态鲁棒性，结果表明，地铁与公交站点的耦合能够显著提高复合网络的鲁棒性；林兆丰等[9]针对地铁-公交复合网络，提出一种基于换乘的加边策略，可以显著提高复合网络遭受攻击时的系统鲁棒性。在复合网络的关键站点识别方面：汪军等[10]提出一种基于贪心介数的关键站点识别方法，鲁棒性实验表明，相比于基于度中心性和介数中心性的攻击策略，贪心介数策略攻击对网络性能影响最大；TANG等[11]以出行量作为权重，运用D-S证据理论识别复合网络中的关键地铁站点；KOPSIDAS等[12]综合考虑地铁站点的复杂网络指标以及失效后的乘客出行时长的变化，提出一种地铁站点重要度计算方法。

综上所述，目前对地铁-公交复合网络的研究存在以下两点不足：一是，现有研究大都停留在分析无权网络特性，没有考虑地铁与公交系统之间差异性；二是，当前研究通常仅考虑复合网络中节点之间的连通关系，而忽略了节点之间换乘关系。基于此，本文综合考虑地铁与公交的运行特性及换乘特性，以出行时间作为边权，构建地铁-公交加权复合网络。并基于加权复合网络特性，构建关键站点的识别方法及其改进的鲁棒性分析模型，分析复合网络在不同攻击模式和攻击策略下的网络鲁棒性。

1 地铁-公交加权复合网络构建

1.1 构建单一模式子网络

为更好地反映公共交通网络的实际空间结构及换乘特性，本文考虑地铁及公交线路上下行的差异性以及同站台站点的差异性，采用Space L 方法[13]构建地铁及公交的有向网络。在网络构建过程中，对于同一线路上下行具有相同名称的站点视为同一站点，对于不同线路具有相同名称的站点视为不同站点。基于以上假设，地铁和公交网络可以分别表示为Gmetro=(Nmetro,Emetro∪Emetro,transfer)、Gbus=(Nbus,Ebus∪Ebus,transfer)。其中，Nmetro和Nbus分别为地铁和公交的站点集合；Emetro和Ebus分别为地铁和公交的站段边集合，用于表征各条线路相邻站点的联系；Emetro,transfer和Ebus,transfer分别为地铁和公交的换乘边集合，用于表征不同线路具有相同名称站点的换乘关系。

1.2 构建地铁-公交复合网络

在实际出行过程中，乘客可以通过步行在地铁与公交站点之间进行换乘，实现公交网络与地铁网络的耦合。现有研究大多基于欧式距离判定换乘距离建立耦合关系[14]，忽略了实际道路网络的结构，可能会造成实际步行距离远大于计算距离的情况。基于此，本文提出一种地铁公交换乘边构建方法，如图1所示，具体步骤如下。

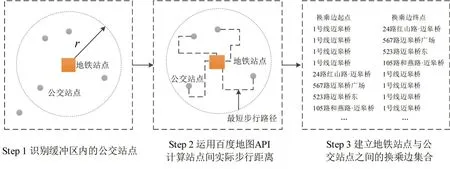
图1 地铁公交换乘边构建方法Fig.1 Method of metro-bus transfer edge construction

Step 1 以地铁站点为圆心建立半径为r的缓冲区，采用GIS(Geographic Information System)空间连接方法识别地铁站点缓冲区范围内的公交站点，建立地铁站点与缓冲区范围内公交站点集合的空间映射关系。

Step 2 调用百度地图API (Application Programming Interface)计算地铁站点与缓冲区范围内每个公交站点的实际步行距离，若计算的实际步行距离大于半径r，则将相应的公交站点剔除集合，更新空间映射关系。

Step 3 基于Step 2所得到的空间映射关系，建立地铁站点与公交站点的换乘边集合。

基于上述地铁公交换乘边构建方法，可以实现地铁与公交网络的复合。复合网络可表示为Gmerge=(Nbus∪Nmetro,Ebus∪Ebus,transfer∪Emetro∪Emetro,transfer∪Emetro-bus)。其中，Gmerge为地铁-公交复合网络，Emetro-bus为地铁站点与公交站点之间的换乘边集合。

1.3 复合网络连边赋权

为真实地反映地铁及公交各自的实际运行特性，本文以出行时间作为连边权重，综合考虑车辆发车间隔、运行速度以及乘客步行距离等因素，建立地铁-公交加权复合网络。如图2 所示，在该加权网络中，包含3类连边，分别为：地铁与公交站段边(Emetro和Ebus)、同种交通方式之间换乘边(Emetro,transfer和Ebus,transfer)及不同交通方式之间换乘边(Emetro-bus)。

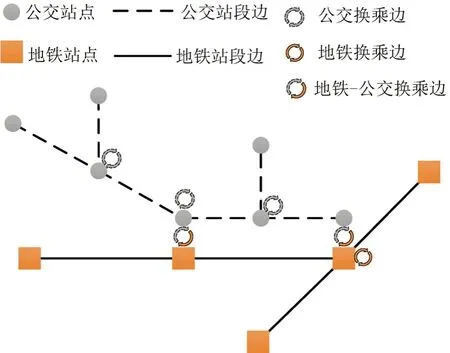
图2 地铁-公交复合网络各类连边示意Fig.2 Different types of edges in metro-bus composite network

对于地铁与公交站段边的时间权重计算。首先，通过分析地铁与公交各线路的历史进出站时间数据，按线路提取公交车辆在线路上到达每一站点的到站时间；然后，计算各站段间的平均行程时间；最后，建立与地铁与公交线路的站段边集合一一对应的站段边时间权重集合Wbus和Wmetro。

对于同种交通方式之间换乘边的时间，其权重为乘客同台换乘的平均候车时间。以公交网络为例，获取各公交线路的历史发车时间数据，针对任意1条公交换乘边，其换乘边的权重[15]为

式中：bi为换乘前的公交站点，bj为换乘后的公交站点，bi与bj的地理位置相同但分属不同线路；Wbus,transfer(bi,bj)为该换乘边的时间权重；blinej为公交站点bj所属的公交线路；为公交线路blinej发车时间间隔实测数据集合；为公交线路blinej发车时间间隔实测数据的平均值；为公交线路blinej发车时间间隔的方差。基于该方法，可以得到与公交换乘边集合Ebus,transfer所对应的换乘边时间权重集合Wbus,transfer。同理，可以获取地铁换乘边集合的时间权重集合Wmetro,transfer。

对于不同种交通方式之间换乘边的时间权重，其由两部分构成：一是，乘客步行至站点的步行时间；二是，乘客在站点换乘的平均候车时间。以公交换乘地铁为例，其换乘边的权重为

式中：mi为换乘前的地铁站点，mi与bj在地理上的实际步行距离小于半径r；Wmetro-bus(mi,bj)为该换乘边的时间权重；K(mi,bj)为通过百度地图API 计算得到的站点间的实际步行距离；Vwalk为乘客的平均步行速度。基于该方法，可以得到与地铁-公交换乘边集合Emetro-bus所对应的换乘边时间权重集合Wmetro-bus。

2 加权复合网络站点重要度评估指标

本文基于所构建的地铁-公交加权复合网络，提出可达重要度、中心重要度以及路径重要度这3 类站点重要度评估指标。其中，可达重要度对网络节点度值[4]的定义进行了拓展，综合考虑复合网络中站点与线路之间的从属关系，能够更加全面地反映站点的间接可达范围；中心重要度以及路径重要度对复杂网络理论中的接近中心性[12]和介数中心性[10]进行改进，所不同的是考虑了出行时间对站点间最短路径的影响，而非简单的基于边数量进行考量，能够更加真实地反映乘客出行路径的选择过程。

(1)可达重要度

站点的可达重要度反映可到达的站点范围。可达重要度越高的站点往往是多条线路的换乘站点，因此，汇聚更多的换乘客流。若其发生失效可能会引起客流出行路径的转变，影响乘客的总体出行效率。在本文中，站点的可达性重要度可以表示为其能够直接到达的站点数量之和，即

式中：Ai为站点i的可达重要度；u为与途径站点i或者与站点i存在换乘连边的公交及地铁线路数量；l(j)为线路j所包含站点数量。

(2)中心重要度

站点的中心重要度反映站点与到达其他节点的便利程度。中心重要度较高的站点通常在空间上位于复合网络中的中心位置，到达其他站点的出行耗时也较短。在本文中，站点的中心重要度可以表示为站点到达复合网络中所有其他可达站点的平均时间的倒数，即

式中：Ci为站点i的中心重要度；σij为在地铁-公交加权复合网络中，站点i到站点j是否存在可达路径，若存在，σij为1，否则，为0；tij为在站点i到站点j之间的最短耗时。

(3)路径重要度

站点的路径重要度反映站点在地铁-公交加权复合网络中作为中间“桥梁”的重要程度。路径重要度更高的站点会汇聚更多的断面客流，若发生失效瘫痪可能会导致大量乘客更换出行线路。在本文中，站点的路径重要度可以表示为站点在复合网络中作为耗时最短的路径被经过的比例，即

式中：Pi为站点i的路径重要度；σst为站点s和站点t是否存在可达路径；为在站点s和站点t之间耗时最短的路径是否经过站点i，若经过，为1，若不经过或者不存在可达路径，为0。

3 加权复合网络鲁棒性分析模型

3.1 攻击方式及攻击策略

本文结合公共交通实际运行过程中所能遇到的突发情况，考虑两类针对复合网络节点的攻击方式，如图3所示。在第1类攻击方式下，受攻击的节点以及所有与其相连的连边均予以删除，该方式常见于恐怖袭击和大规模的交通事故等情形。在第2类攻击方式下，删除受攻击的节点以及所有与其相连的换乘连边，同时，与之相连的站段连边越过该站点直接连接，该方式常见于站台事故造成的无法停靠和重大活动期间的人流管控等情形。

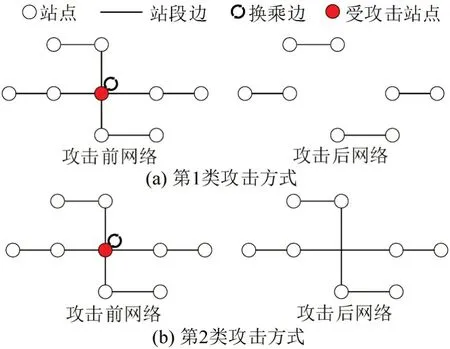
图3 两类攻击方式Fig.3 Two types of attack modes

在攻击策略方面，本文采用随机攻击和蓄意攻击两种方式。随机攻击完全随机的删除复合网络中一定数量的节点。蓄意攻击根据分别基于可达重要度、中心重要度及路径重要度由大到小的排序，有针对性地删除网络中一定数量的节点。

3.2 鲁棒性度量指标

现有研究大多采用网络最大连通度以及网络效率衡量度量网络的鲁棒性[6-11]。本文在此基础上，结合所构建的加权复合网络，改进网络效率的计算方法，采用出行时间度量节点之间的网络效率，可以更加真实地反映节点间的真实物理距离以及不同交通方式速度上的差异性。此外，本文还提出绕行比例这一新指标，用于反映网络在遭受攻击后客流的路径更改比例，具体指标如下。

(1)网络最大连通率

网络最大连通率定义为当网络遭受攻击时，所分离的最大连通子图的节点数量与初始网络节点数量的比例，即

式中：S为网络最大连通率；|N|为原始网络的节点数量；|N′ |为受攻击后最大连通子图的节点数。

(2)网络效率

网络效率定义为所有可达OD 对的最短出行耗时倒数之和的平均值，即

式中：F为网络效率；Q为复合网络中所有可达的OD对数量。

(3)绕行比例

绕行比例定义为由于网络遭受攻击所造成的最优路径发生变化的比例，即

式中：R为绕行比例；ak为第k个OD 对的最优路径是否变更，ak=0 表示最优出行路径未受影响，ak=1表示需要绕行或不可达。

4 实例分析

本文以南京的地铁和公交网络为例，对复合网络的关键站点进行识别及其鲁棒性进行分析。研究区域选取南京公交集团公交线路所覆盖的8 个区，不包含江宁区、溧水区和高淳区。研究区域内包含地铁站点120 个，公交站点4266 个，涉及地铁线路7 条，公交线路439 条。基于南京市实际线网和运行数据，构建地铁-公交加权复合网络。其中，站段边以及换乘边的权重采用2021 年5 月日均运行数据的平均值；地铁站点缓冲区半径设置为500 m[7]；乘客的步行速度设置为5 km·h-1。研究范围如图4所示。

图4 地铁公交网络研究范围Fig.4 Research scope of metro and bus network

4.1 加权网络网络特性分析

加权复合网络与加权子网络的网络特性对比如表1所示。从网络节点的数量来看，由于在网络建模过程中考虑了换乘节点的差异性，因此，网络的节点数量要高于实际站点数量。具体来看，地铁网络由于换乘站点较少，网络节点与实际站点数量相差不大。对于公交网络和复合网络而言，由于存在大量公交换乘站，因此，网络节点数量远远高于实际站点数量，平均每个站点约有2.6条线路经过。

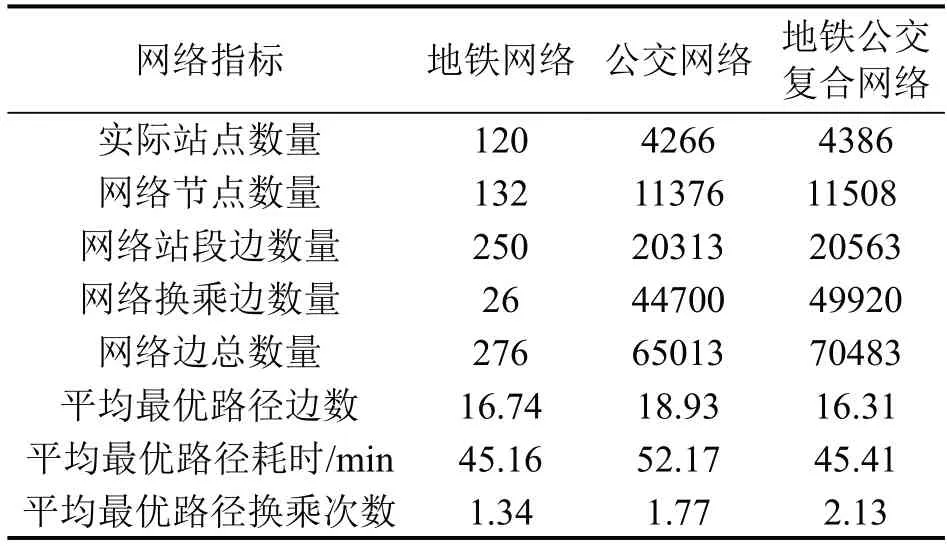
表1 加权复合网络与加权子网络的网络特性比较Table 1 Network characteristics comparison between weighted compound network and sub-networks

从网络边的数量来看，地铁网络大多为站段边，换乘边数量较少。公交网络存在大量的同台换乘连边，换乘边约为站段边数量的2.2 倍。复合网络在子网络组合的基础上增加了地铁-公交换乘边，平均每个地铁站点约与21.6个公交站点存在耦合换乘关系。

在最优化路径方面，本文采用Dijkstra算法，以出行时间最短为目标求解加权网络各可行OD 的最优路径。

从表1可知，复合网络在最优路径边数上要低于地铁网络和公交网络，同时，在最优路径换乘次数方面要高于两者。这是因为在复合网络的路径规划中，可以充分利用地铁大站距、运行速度快以及换乘时间短的优势，通过组合出行减少整体出行时间。经分析，在复合网络所有的最优路径中，公交地铁组合出行的比例高达56%。得益于此，复合网络最优路径的平均耗时相比于公交网络减少了约13%。

4.2 加权复合网络关键站点识别结果

基于本文所提出的站点重要度计算方法，识别加权复合网络的关键站点。

由表2 可知，对于可达重要度、中心重要度以及路径重要度排名前50 名的站点，地铁站点分别占比60%，80%以及98%。表明地铁网络虽然在规模上远小于公交网络，但在地铁-公交复合网络中扮演着更为重要的作用。

表2 加权复合网络站点重要度统计分析结果Table 2 Statistical analysis results of station importance for weighted compound network

对于可达重要度，其均值为80.94，表明在复合网络中平均每个站点可与约81个站点存在直达关系。可达重要度的中位数为48.75，远低于其均值，表明复合网络中站点可达性分布极不均衡，高可达性的站点虽然占比小，但提升了网络总体的可达性。从图5可以看出，可达重要度排名前50的站点大多为区域内的换乘枢纽节点，周边公交站点覆盖稠密，可以为多线路间换乘提供桥梁作用。

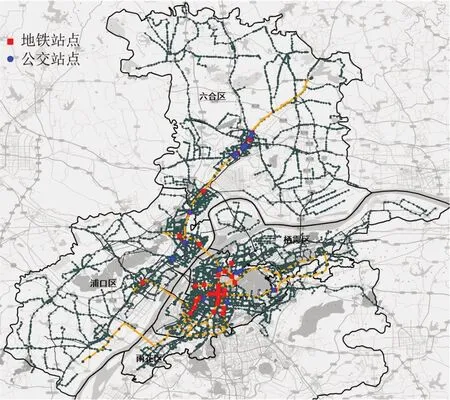
图5 可达重要度前50站点空间分布Fig.5 Spatial distribution of top 50 stations rank by accessibility importance

对于中心重要度，其均值为0.022，表明复合网络中平均每个站点到其他站点的平均耗时约为45.4 min。从空间分布上来看，如图6所示，中心重要度较高的站点几乎均集中在城市中心的主城区域，通常为地铁站点或与地铁站点相邻的公交站点，可以充分利用地铁网络的快捷性到达复合网络中的其他站点。

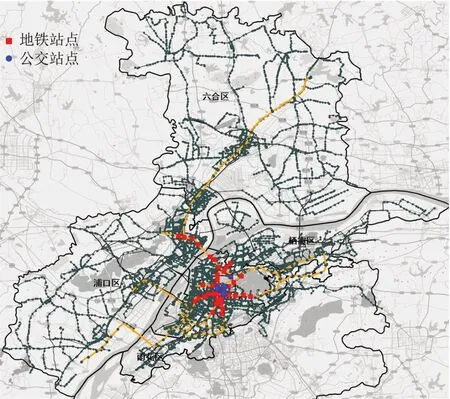
图6 中心重要度前50站点空间分布Fig.6 Spatial distribution of top 50 stations rank by centrality importance

对于路径重要度，其最大值为0.2115，表明在复合网络中约21.15%的最优路径需要经过该站点。该值远高于其均值及中位数，表明在复合网络中少量站点具有较高的路径重要度。由图7 的空间分布可以看出，前50的站点几乎均为地铁站点，主要分布于公交网络较为密集的主城区域。此外，在浦口区和六合区部分地铁站点也具有较高的路径重要度，这些站点通常作为换乘站点与周边公交相衔接，通过组合出行实现与主城区域站点的快速连接。

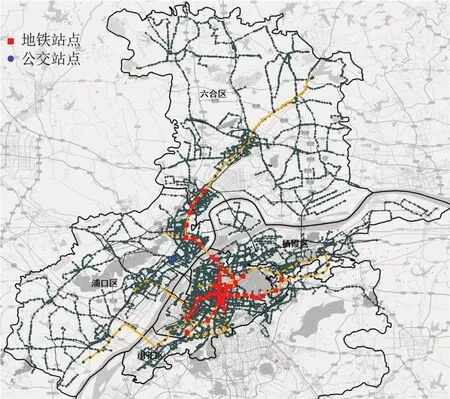
图7 路径重要度前50站点空间分布Fig.7 Spatial distribution of top 50 stations rank by path importance

4.3 加权复合网络鲁棒性仿真分析

基于所构建的加权复合网络，分别对两类攻击方式进行鲁棒性仿真实验。仿真每次删除网络中20个站点，蓄意攻击按照站点的3类重要度排序由高到低依次删除，随机攻击每次随机选择网络中的站点。不同攻击方式下网络绕行比例、最大连通率以及网络效率的变化情况如图8所示。

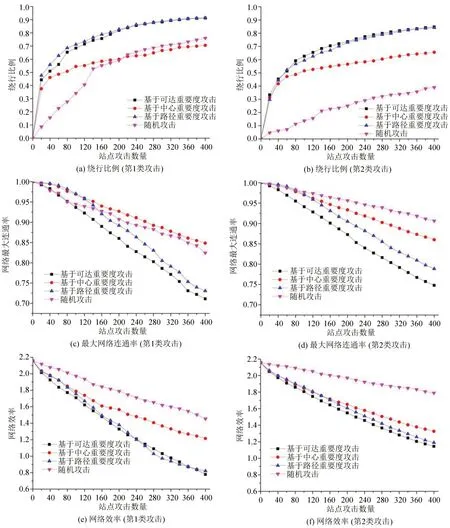
图8 不同攻击方式和攻击策略下复合网络鲁棒性指标变化情况Fig.8 Variation of robustness metrics under different attack methods and strategies

对于第1类攻击方式，可以看出：

(1)在基于路径重要度的攻击策略下，绕行比例增长最快。而在基于可达重要度的攻击策略下，网络的最大连通度下降最快。从侧面体现两种攻击策略的特点，即基于路径重要度的攻击重点是最优路径中途径比例更高的站点，而基于可达重要度的攻击重点是网络中连通度较高的枢纽站点。两种攻击策略对于网络效率的影响均显著高于基于中心重要度的攻击以及随机攻击。两者网络效率的演化曲线呈现多处交叉，当受攻击站点数量达到400时，网络的平均效率仅为初始网络的36%。

(2)当受攻击站点数量较少时，蓄意攻击策略下的绕行比例增长迅速，40个站点的失效会导致超过55%的出行需要绕行，但网络的最大连通度变化却并不显著。主要是因为蓄意攻击在前期主要的攻击对象是复合网络中的地铁站点，虽然，地铁站点规模在复合网络中仅占2.7%，但是，却起到了重要的快速通道作用，在最优路径中的占比高达57%，因此，地铁站点的失效会显著增加网络的绕行率。但由于地铁站点往往与多个公交站点存在耦合关系，因此，地铁站点的失效并不会对复合网络的整体连通性产生较大影响。

(3)基于中心重要度的攻击对网络鲁棒性的影响要弱于其他两类蓄意攻击。甚至在网络连通度以及绕行比例方面，攻击效果要弱于随机攻击。主要是因为中心重要度较高的站点集中于公交线网密度较高的城市中心区域，站点失效时可替代的出行路径相较于城市外围区域更多，因此，对网络连通度的影响较小。此外，中心重要度较高的站点往往集中于少量线路，而针对同一线路中站点的集中攻击难以对更多的出行路径产生持续影响，因此，当攻击站点数量超过一定值时，对绕行比例的影响要弱于随机攻击。

相比于第1 类攻击方式，第2 类攻击方式下的网络鲁棒性呈现以下特点：

(1)第2类攻击方式下，复合网络具有更强的鲁棒性。以基于可达重要度的攻击为例，当攻击站点数量为400时，相较于第1类攻击方式，第2类攻击的绕行比例减少了7.1%，网络最大连通度以及网络效率分别提升3.7%和52.2%。主要是因为在第2类攻击方式下，站点的失效并不会造成线路整体的断开。因此，当攻击站点在出行路径中并非出行首末站点或换乘站点时，站点的失效并不会影响出行路径。

(2)基于可达重要度的攻击策略对网络性能的影响最大。主要是由于可达重要度较高的站点大多是区域内的换乘枢纽站点，其失效会显著的影响网络的整体连通率，造成出行失败或长距离绕行，因此，对网络效率影响更大。

(3)随机攻击策略下的网络鲁棒性提升明显，各项鲁棒性指标显著优于蓄意攻击策略。

5 结论

本文综合考虑地铁与公交在实际运行上的差异性以及站点间的换乘特性，以出行时间作为权重，提出一种更加贴合实际的地铁-公交加权复合网络构建方法。并针对所构建的加权复合网络，提出新的站点重要度评估方法以及改进的鲁棒性评估模型。以南京市为例，分析加权复合网络的网络特性、关键站点以及鲁棒性，得到的主要结论如下：

(1)在地铁-公交复合网络中，尽管地铁网络规模远小于公交网络(地铁站点数量仅占2.7%)。但由于其运行速度快和换乘时间短，在复合网络中起到区域间的快速通道作用，能够从整体上极大地提升复合网络的运行效率。研究表明，在复合网络的最优路径中，公交地铁组合出行的比例高达56%，最优路径的平均耗时相比于单一的公交网络减少了约13%。

(2)地铁站点对复合网络鲁棒性的影响要远高于公交站点。在可达重要度、中心重要度以及路径重要度排名前50 名的关键站点中，地铁站点分别占比60%，80%以及98%。当关键地铁站点遭受攻击时，会造成复合网络绕行率的迅速提升以及网络效率的快速下降，但由于其与公交网络的衔接紧密，对复合网络的整体连通性影响较小。

(3)在复合网络遭受第1类攻击方式时，基于路径重要度的攻击策略对网络的绕行比例影响最大，基于可达重要度的攻击策略对网络的最大连通度影响最大。两者对网络效率的影响随着攻击站点数量的提高，出现交替领先的现象。基于中心重要度的攻击策略由于攻击区域以及线路分布集中，对复合网络鲁棒性的影响相对较小。

(4)相较于第1类攻击，复合网络在第2类攻击下表现出更强的鲁棒性。具体而言，蓄意攻击对网络的破坏能力要显著强于随机攻击策略，基于可达重要度的攻击策略对网络性能影响最大。