考虑减排的公交线网分时差异化票价动态优化

李雪岩，李海洋，张汉坤

(1.北京联合大学，管理学院，北京 100101；2.北京工商大学，电商与物流学院，北京 100048)

0 引言

2022年，交通运输部印发了《贯彻落实〈中共中央、国务院关于完整准确全面贯彻新发展理念做好碳达峰碳中和工作的意见〉的实施意见》，《实施意见》指出：要“鼓励运输企业积极拓展多样化公共交通服务，提高公共交通供给能力，完善绿色出行服务体系，引导公众优先选择绿色出行方式”。可见，“双碳”背景下，低碳出行的变革需要长期综合施策。目前，已有研究表明，价格调节是提升运力资源配置科学性的重要经济手段，在提升运营收入及合理引导个体机动化出行方面具有重要作用。赵雪峰等[1]通过改进的机器学习模型分析与出行全过程相关的因素对定价的影响发现，每日搭乘时间周期性影响定价。CHEN等[2]评估不同票价政策对出行模式的影响发现，票价政策变化是引发出行流量变化的重要因素。ZHANG 等[3]在静态需求条件下，建立地铁与共享单车的整合运营模型优化票价，发现不同出行方式的协调运行有助于降低社会成本。邓连波等[4]在静态需求条件下，以降低社会成本为目标，针对不同公交线路进行差异化定价，实现价格杠杆的客流调节功能。李雪岩等[5]在静态需求条件下，将线路差异化票价优化拓展为多目标优化问题，并引入乘客的有限理性因素。进一步，LI等[6]在静态需求条件下，将出发时间差异纳入定价因素，建立多目标分时票价优化模型，发现社会互动行为会影响行程时间。另一方面，针对城市交通的减排问题，朱顺应等[7]建立排放效率评价模型，发现公交线路的运行速度(行程时间)变化会影响碳排放效率。吕莹等[8]发现，在竞争作用下，网约车、公交及地铁等不同出行方式出行量的变化会产生不同的能源环境效应。可见，价格因素可以通过出行量的变化影响排量，但价格视角下的公交系统减排研究却不多见。

目前，大型城市交通系统的节能减排和拥挤疏解等问题已成为全社会的长期战略，值得从物理和经济等多种视角进行尝试研究，通过梳理文献可知，作用于公交系统的经济手段仍可针对以下问题深入研究：既有研究大多将票价调节视为静态优化问题，易忽略OD间需求的动态变化(例如工作日与周末的差异)，在线网内流量的叠加作用下，则会影响价格方案实施的有效性；考虑减排目标，运用价格杠杆对时间与线路进行差异化处理，寻找同时降低线网系统碳排放与社会成本的帕累托最优解。

针对上述问题，本文在既有研究的基础上开展以下工作：(1)考虑OD间出行需求的动态变化过程与出发时间差异，设置降低碳排放与降低社会成本两个目标函数，引入社会交互机制与后悔理论刻画出行者的有限理性，将分时差异化票价作为优化变量，构建动态多目标优化模型；(2)将基于BP神经网络的种群分布预测算子、OD 矩阵均衡算法以及静态多目标粒子群算法进行有机结合，构建新的集群智能动态多目标优化算法求解模型，达到利用价格杠杆降低排放和提升公交线网效率的目的。

1 问题提出与线网状态描述

1.1 问题描述

1.2 线网状态描述

2 出发时间与出行方式选择模型

2.1 出发时间选择

结合人们在现实中的出行习惯，将出发时间的选择视为一个损益判断过程。借鉴文献[6]中的出发时间价值函数构造方式及其对基准时间的定义，令Te，Tb，Tl分别表示“可接受的早到时间”(早于该时间到达目的地意味着遭受损失)，“预计到达时间”(在该时间到达获得最大效用)及“迟到时间”(晚于该时间到达目的地意味着遭受损失)，给定出行方式m，第t日站点i,j间出行者选择τ时刻出发的效用为

式中：λ1～λ4为损失厌恶程度；α1,α2,β1,β2为风险敏感度。进一步，出行者通过各类智能设备获取不同选择可能得到的效用，因此，运用后悔理论刻画实际效用值，出发时间τ的后悔成本表示为函数ϕ(x)=1-exp(-δx)，δ为后悔厌恶水平，θ为效用感知系数，则站点i,j间选择出发时刻τ的人数为

2.2 出行方式选择

出行方式选择受到以下因素影响：

(1)票价与停车费。

(2)等待时间

(3)行程时间

(4)拥挤度

(5)外界信息学习效应

综上，第t日站点i,j间在出发时间τ选择出行方式m的广义费用为

3 分时OD矩阵均衡算法

给定站点间出行需求di,j(t)，分时差异化公交票价Pr(τ)，停车费及公交发车频率fr(r∈R,τ∈{τ1,τ2,…,τS})后，经过式(3)和式(5)的迭代，线网形成与优化变量对应的OD矩阵。迭代算法如下。

Step 0 确定每个OD 对之间的可行线路与换乘线路。

Step 3 依据式(2)和式(4)计算不同出发时间与出行方式的广义效用/费用矩阵。

Step 4 依据式(3)和式(5)更新OD 矩阵，得到

显然，具有时变特征的di,j(t)以及出行行为因素的变化会使发生均衡转移。

4 分时差异化公交票价动态多目标优化模型

由分时OD矩阵均衡算法与式(6)可见，与静态多目标优化问题不同，站点i,j间的出行需求di,j(t)具有时变特征，因此，运营政策(决策变量)的实施应尽量针对需求环境D(t)的变化具有预判性，而并非在已知固定需求的基础上给出相对滞后的政策(会影响票价政策实施的有效性)，综上，式(6)构成典型的动态多目标优化问题。

5 模型求解算法

针对上述动态多目标优化问题，将基于模块化神经网络的新种群分布预测算法、OD 矩阵均衡算法以及具有优秀性能遗传算子的静态多目标粒子群算法进行有机结合，构建新的集群智能动态多目标优化算法求解模型。算法步骤设计如下。

Step 1 粒子群初始化。设置粒子群(种群)规模为Na，粒子群每个个体在决策变量约束区间内随机取值，粒子i′对应的优化变量为Xi′=[P1,i′(τ1),…,P1,i′(τS),…,PR,i′(τ1),…,PR,i′(τS),f1,i′,…,fR,i′] 。粒子个体i′存放非支配解的集合表示为Bi′，全局非支配解集表示为Bu。

Step 2 初始化模块BP神经网络。

Step 3 计算目标函数值。对于种群内每个个体i′，计算Xi′对应的OD均衡矩阵qm(t,τ)，继而依据式(6)计算目标函数值

Step 4 判断需求环境是否变化。定义ΔD=‖D(t)-D(t-1) ‖与需求环境阈值σD。

情况1 如果ΔD ＜σD，即需求环境未发生变化，则按照以下步骤对粒子群进行优化。

情况2 如果ΔD≥σD，即需求环境发生了变化。

如果当前的需求环境D(t)之前没有出现过，则基于文献[9]的方法，用D(t-1) (输入)与当前种群(X1,…,Xi′,…,XNa)(输出)训练内置BP 算法的神经网络；如果当前的需求环境D(t)已经出现过，则直接用D(t)作为神经网络输入，输出新种群(X1,…,Xi′,…,XNa)。

由Step 4 得到的种群表示为P4。

Step 5 帕累托前沿中心点预测。令Xc′表示由种群(X1,…,Xi′,…,XNa)所构成帕累托前沿的中心点，则Xi′,t+1=Xc′,t-Xc′,t-1+Xi′,t+G(0,d′),1 ≤i′≤Na，其中，G(0,d′) 表示高斯扰动，Xi′,t+1(1≤i′≤Na)构成的种群表示为P5。

Step 6 种群内随机选择一定比例的粒子，在决策变量约束区间内随机取值，这些粒子表示为P6。

Step 7 从P4，P5，P6中选出Na个粒子形成新种群，按照Step 4.1～Step 4.5 对种群进行一轮优化，得到帕累托最优解Ps。

Step 8 若不满足停止条件，则返回Step 3；否则，输出当前最优解Ps。

算法流程如图1所示。

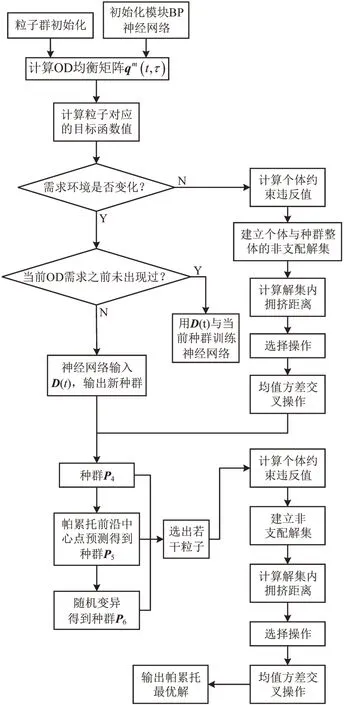
图1 算法流程Fig.1 Algorithm flow chart

6 算例分析

6.1 算例路网及参数

以Mandl路网为例分析本文模型，站点间的行程时间和需求等数据依据文献[10]取值，运用OD需求在工作日与双休日的差异性表示D(t)的连续动态变化过程(5个工作日+双休日)，取北京市公交线路站点间工作日与双休日的出行需求差异比例1.00∶0.72，模拟算例路网中站点间的OD 需求变化。算例路网如图2所示，图中圆圈内数字为站点编号，连线上数字表示行程时间(min)。

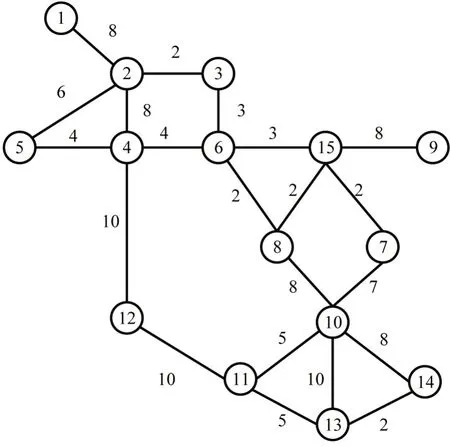
图2 算例路网Fig.2 Road network

路网中既有公交线路由文献[10]给出的线路优化结果得到。

线路1：12-11-10-8-6-4-5-2

线路2：14-10-13-11-12-4-2-1

线路3：9-15-7-10-8-6

线路4：1-2-3-6-8-15-7-10

核心变量符号与模型主要参数取值如表1所示。

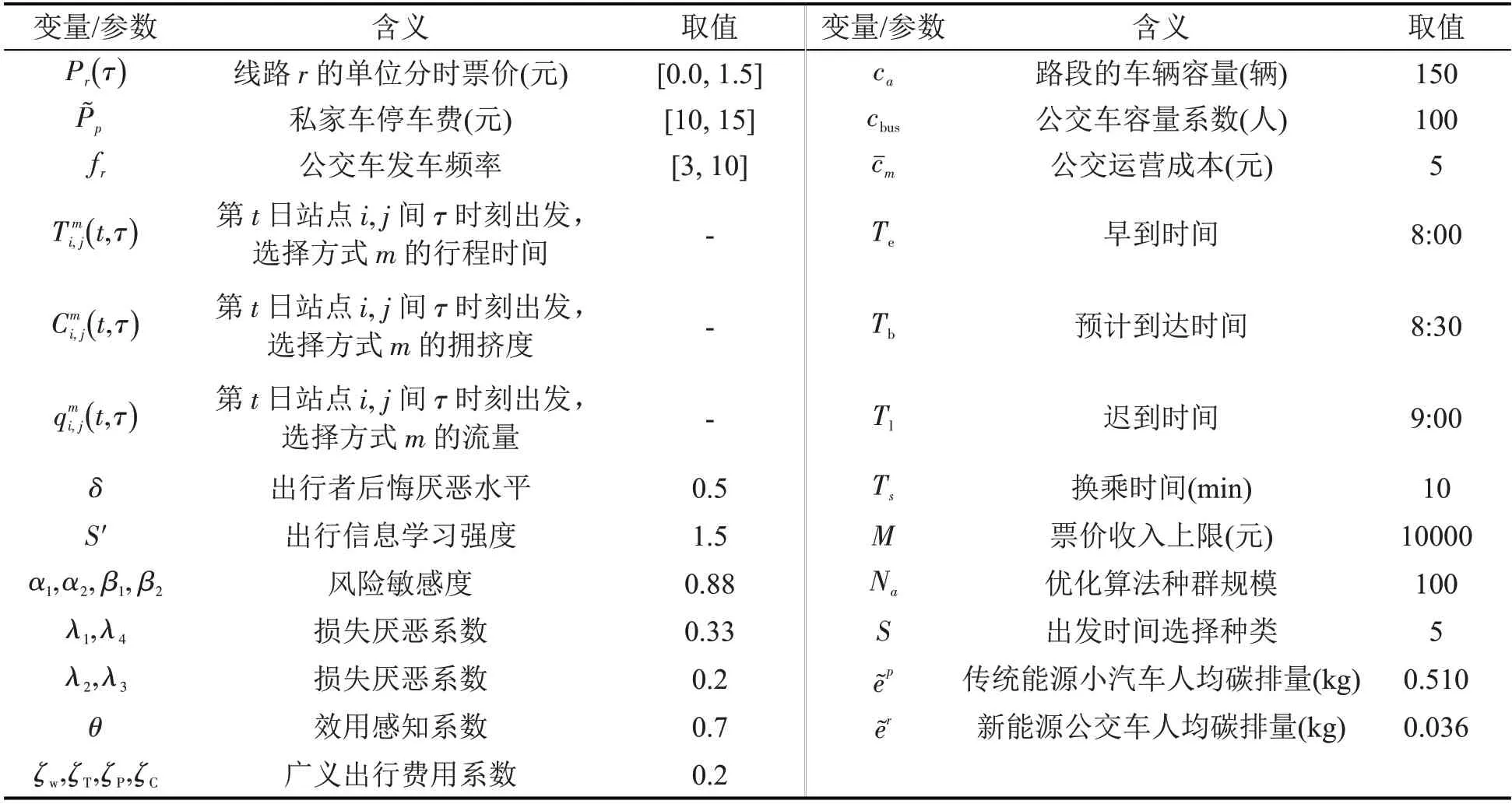
表1 核心变量说明及模型参数取值Table 1 Explanation of core variables and values of model parameters

表1 中，δ与S′依据文献[5]取值，依 据文献[4] 提供的成本水平与数量级取值，α1,α2,β1,β2,λ1～λ4依据文献[6]取值，与取自网络公开的新能源公交车与传统能源小汽车每人每公里碳排放数据，算法运行环境为matlab2019。

6.2 优化结果

多目标动态优化算法迭代趋于稳定时，分时差异化票价可行解对应的帕累托前沿如图3所示，图3中，“周末”与“工作日”迭代步数之差仅为2(周日与周五)，说明算法中种群对需求环境的变化具有较强的敏感性，同时，也说明di,j(t)的变化使OD间的流量结构产生均衡转移。代表性帕累托最优解对应的分时差异化票价、发车频率以及停车费的求解结果如表2 所示。由图3 结合表2 可知，碳排量较低的帕累托最优解(D3，E3)对应的票价总体水平也较低，碳排量较高的帕累托最优解(D1，E1)对应的票价总体水平则较高，这是由于，当公交票价水平较低时，对乘客的吸引力增加，起到了鼓励公交出行的作用，从而降低了系统整体碳排量。进一步，工作日平均票价降低42.97%(D1～D3)，碳排量可降低22.11%，周末平均票价降低63.91%(E1～E3)，碳排量可降低39.02%。可见，在整体出行需求较小时(周末)下调票价，线网系统内的碳排量下降更加明显，此外，周末出行活动对应的最优解也降低了社会成本，这是由于，相对于工作日，公交在周末具有更低的广义费用(拥挤度明显下降)，加之下调票价，因此，能够进一步吸引客流，降低排量及社会成本。

表2 优化结果Table 2 Optimal results

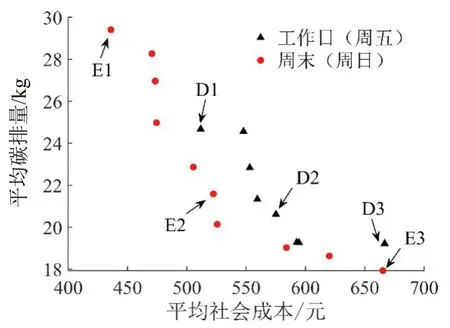
图3 时变帕累托最优解Fig.3 Time-varying pareto optimal solution

6.3 运营方案实施效果分析

在本文可行解与各种固定票制条件下，路网的流量分配及运营方案计算结果如表3 和表4 所示。由表3可见，工作日条件下，相比于各种固定票制，本文模型得到的代表性分时差异化票价方案D2在降低最大断面流量的基础上，提升了平均断面流量，达到同时拥挤疏解与鼓励公交出行的效果。相比于固定票制，方案D1与方案D3使最大断面流量降低4.73%，而平均断面流量仅降低0.56%，在疏解拥挤的同时保证了运营效果。此外，票价方案D1～方案D3 显著降低了不同线路断面流量的标准差，说明分时差异化票制可使线网中不同线路的客流分配更加均衡，避免线路客流分配“冷热不均”的现象。此外，相对于固定票制，虽然票价方案D2和方案D3显著降低了系统平均OD碳排量，但由于其鼓励公交出行的作用，也增加了平均行程时间。由表4 可见，在周末的出行需求条件下，相比于固定票制，本文模型得到的代表性分时差异化票价方案E2 在将平均断面流量维持在较高水平的同时，显著降低了最大断面流量与不同线路断面流量的标准差，从而提升了客流在不同线路之间分配的均衡性，同时，也能够使系统平均OD 碳排量维持在较低水平。票价方案E3在提升平均断面流量和鼓励公交出行的基础上，显著降低了系统平均OD碳排量。由于上述方案鼓励公交出行的作用，也增加了平均行程时间。

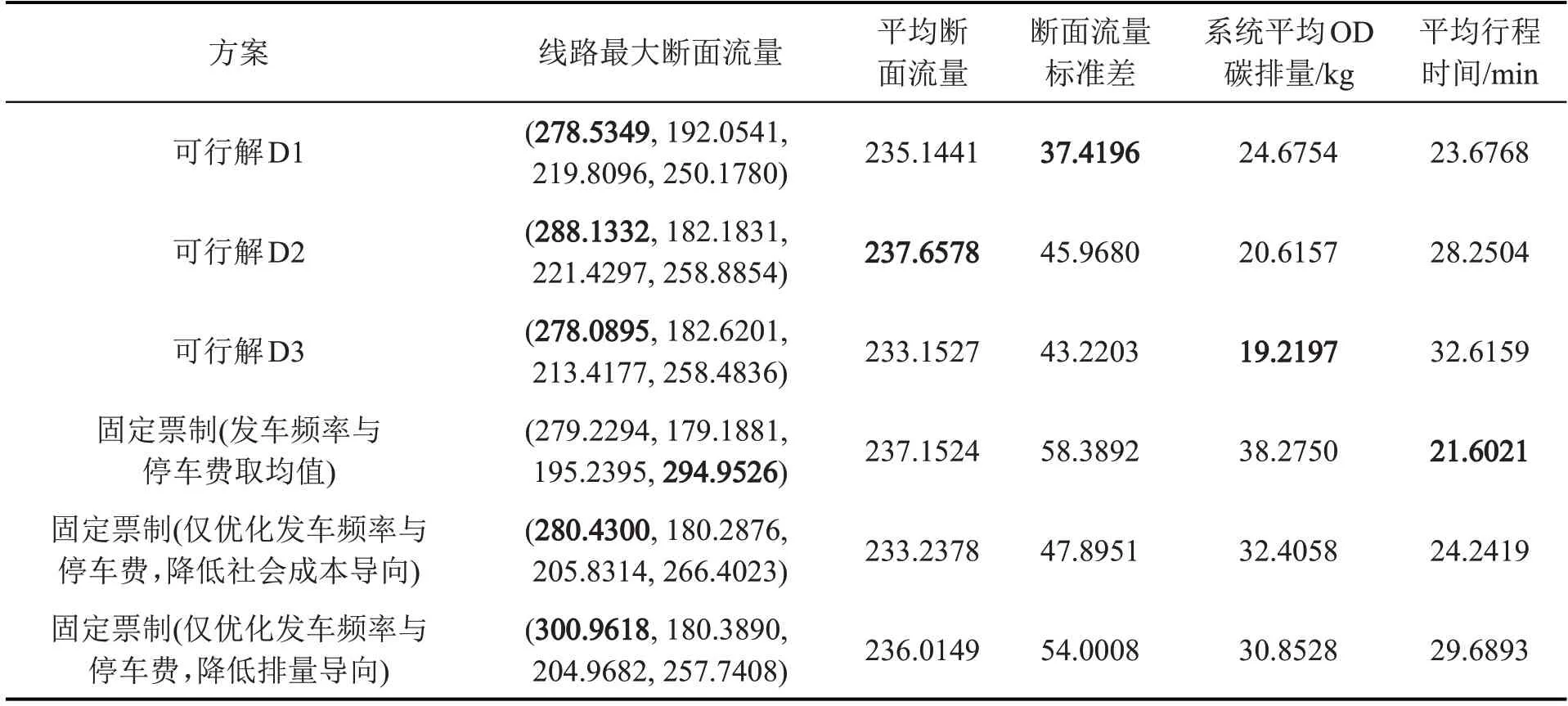
表3 工作日运营方案实施效果对比Table 3 Comparison of weekday operation plans

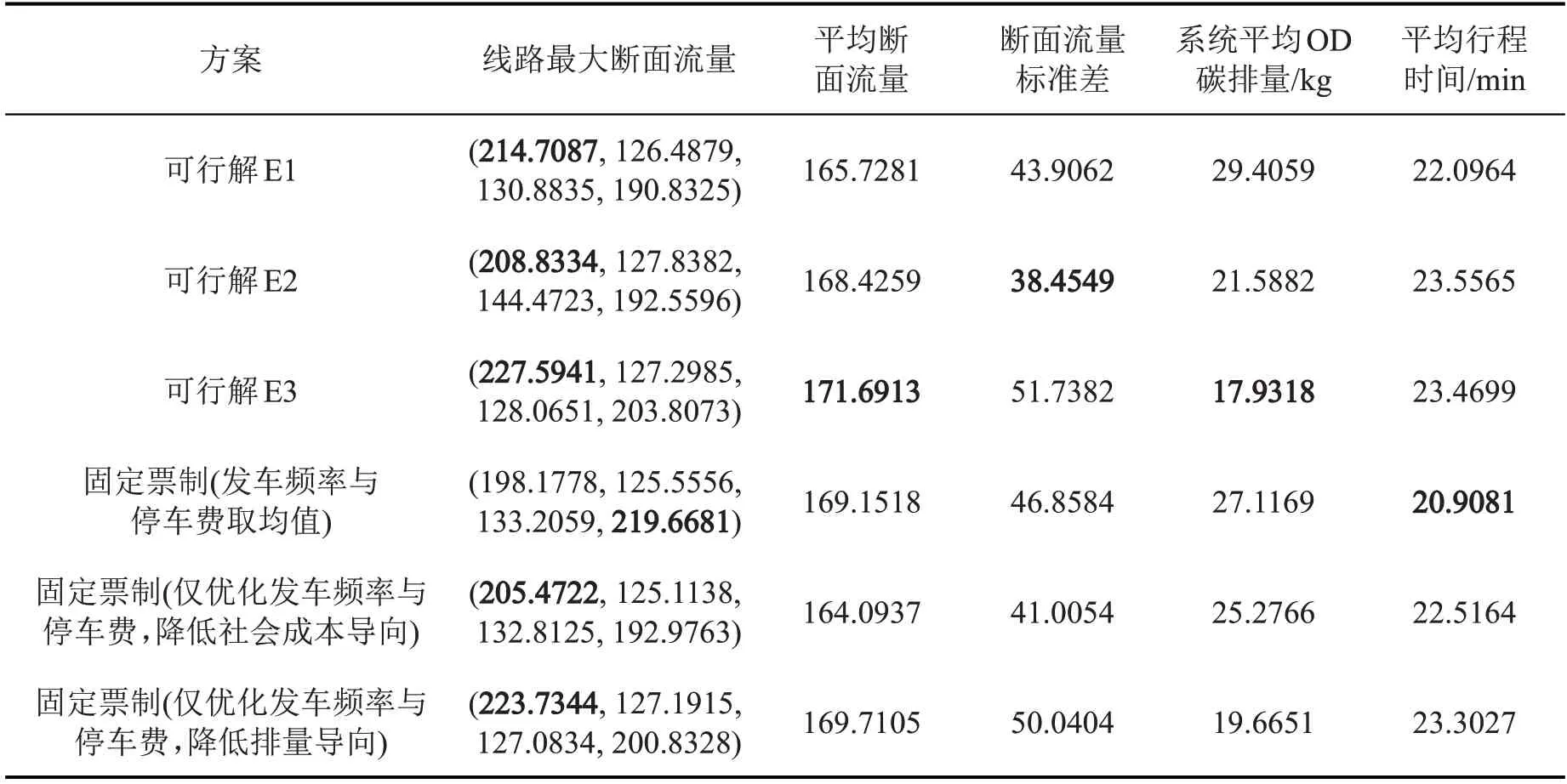
表4 周末运营方案实施效果对比Table 4 Comparison of weekend operation plans

可见，无论是工作日还是周末，相对于固定票制，在不同的分时差异化票制中，均能够产生既降低最大断面流量又提升平均断面流量，且使不同线路之间客流更加均衡的方案。产生这一结果的原因在于：由表2 可知，降低排量的目标函数会产生低票价，以鼓励公交出行，从而使公交平均断面流量增加，与此同时，广义费用是社会成本目标函数的重要组成部分，因此，在较大平均断面流量的基础上，降低社会成本的目标函数则会通过调整不同出发时间以及线路间的价差，降低由拥挤程度构成的广义费用，从而使不同线路之间的客流更加均衡。

不同票制条件下，不同出发时刻选择不同出行方式的客流量运算结果如图4所示，其中，横轴“出行方式”中的数字1～4表示路网中的4条公交线路，数字5 表示私家车。结合表3 与图4(b)和图4(c)可知，由于工作日出行需求较大，相对于不进行任何优化的固定票制，在减排目标的作用下，产生了鼓励公交出行的效果，以降低社会成本为导向的票价方案D1，使系统平均OD 碳排量降低35.53%，使系统内高峰期的最大公交客流量增加4.03%(43.74人)，票价方案D2 使系统平均OD 碳排量降低46.14%，使系统内高峰期的最大公交客流量增加3.99%(43.25 人)。结合表4 与图4(e)和图4(f)可知，由于周末的出行需求较小，相对于不进行任何优化的固定票制，以降低社会成本为导向的分时差异化票价E1 也降低了周末高峰期的最大公交客流量，达到“削峰填谷”的效果，票价方案E2 使系统平均OD碳排量降低20.39%，仅使系统内高峰期的最大公交客流量增加0.5%(3.64 人)。可见，相对于高峰期客流的少量增加，分时差异化票价的减排作用更加明显。

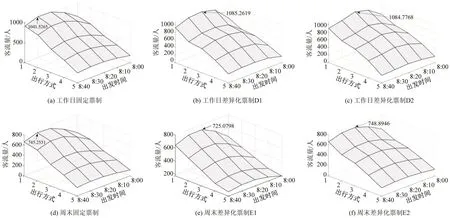
图4 不同票制下客流分配情况Fig.4 Passenger flow allocation under different ticket systems

6.4 运营目标影响因素分析

参照文献[5]对出行者信息学习强度与后悔厌恶水平的取值范围，考察这两个参数对客流分配及动态优化结果的影响。

图5(a)模拟了出行行为因素变化所产生的OD矩阵均衡转移现象，在验证分时OD矩阵均衡算法的同时也说明，在现实情形下，均衡是一种理想状态，出行者的风险态度、信息学习强度变化会对流量结构产生影响。进一步，考察参数对最优解的影响，由图5(b)和图5(c)可知，一方面，增加出行者的信息学习强度，降低了决策的不确定性与信息不对称，可使优化算法得到的帕累托前沿不断向有利于降低社会成本与碳排放的方向移动，另一方面，出行者对风险越厌恶，对做出低效用选择的后悔程度越大，越倾向于做出更加理性的决策，因此，帕累托前沿也会向着利于降低社会成本与碳排放的方向移动。结合信息学习效应的构造方式可知，在实际行业应用中，一方面，首先，运营管理部门通过大数据手段获取出行者群体的风险态度，然后，依托本文模型制定更加具有针对性的票价方案。另一方面，也可以通过及时向出行者推送不同出行方式的流量信息和降低出行选择的不确定性达到同时减少系统碳排放与社会成本的目的。

图5 运营目标影响因素Fig.5 Factors influencing operational objectives

7 实例测算

选取北京市朝阳区国贸附近的实际路网结构作为实例进行测算，该路网包含6 个节点，每个节点附近均有公交站。选择其中具有代表性的线路作为研究对象(线路1：1-2-5-6；线路2：1-4-5-6；线路3：4-5-2-3)，站点间的OD需求由公共交通刷卡数据脱敏获得(采集时间为2020年8月1日～9月30日)，相邻站点之间的行程时间由地图软件获得。实例路网如图6所示。

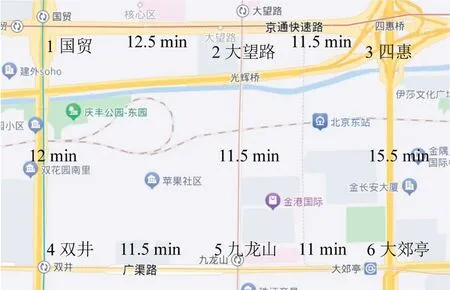
图6 实例路网Fig.6 Real road network

分时差异化票价可行解对应的帕累托前沿如图7 所示，图7 中，典型可行解(兼顾减排目标与社会成本目标)与固定票制条件下，实际路网的运营方案计算结果如表5 所示。由表5 可见，相对于固定票制，工作日与周末的分时差异化票价虽然小幅增加了线路最大断面流量(工作日1.2%，周末1.1%)，但也增加了平均断面流量，起到鼓励公交出行的作用，同时，显著降低社会成本与系统平均碳排量。

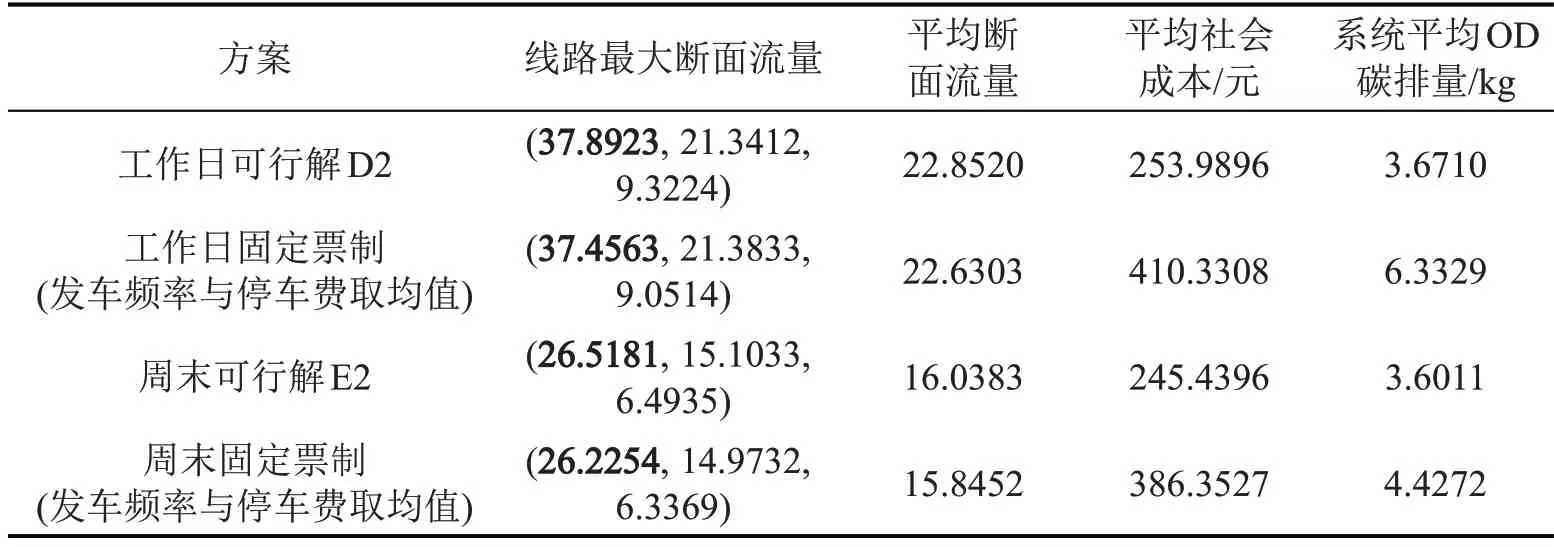
表5 运营方案实施效果对比Table 5 Comparison of weekday operation plans

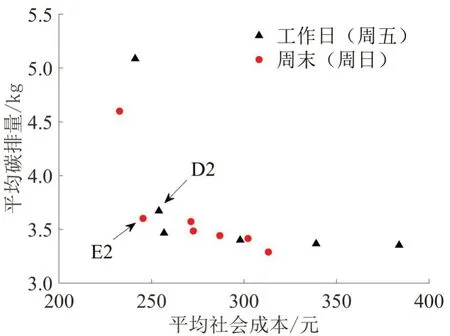
图7 时变帕累托最优解Fig.7 Time-varying pareto optimal solution

8 结论

本文以降低公交线网碳排放与社会成本为目标，综合考虑出行需求在工作日与周末的动态变化、出发时间差异及出行者有限理性，建立分时差异化票价动态多目标优化模型，进一步，将基于BP神经网络的种群分布预测算子、OD 矩阵均衡算法以及静态多目标粒子群算法进行有机结合，构建新的动态多目标优化算法求解模型，运用动态帕累托最优解补充既有票价调节机制，具有可操作性。本文得到的主要研究结论如下：

(1)线网内整体出行需求较小时，实施公交最优分时差异化票价、发车频率及私家车停车费可得到更低的碳排量以及社会成本，而在线网整体出行需求较小时，下调票价，线网内碳排量下降幅度更大。

(2)相对于固定票制，分时差异化票制可以在降低系统平均碳排量的同时起到鼓励公交出行的作用，使线网中不同线路的客流分配更加均衡，避免客流分配“冷热不均”现象。在线网内整体出行需求较小时，分时差异化票制可有效降低高峰期的最大公交客流量，起到拥挤疏解的作用。此外，无论是在工作日还是周末，分时差异化票制均以小幅增加高峰期最大公交客流量的代价实现了系统碳排量的大幅下降。因此，在票价政策的实际实施过程中，可运用差异化的价格杠杆疏解拥挤，降低排量。

(3)在票价政策的实际实施过程中，也可针对出行者群体的风险态度制定具有针对性的票价方案，此外，及时向出行者提供准确的效用信息，可有效减少社会成本与系统碳排放。