基于时间图注意力的交叉口交通状态识别及关联度研究

李鹏程，董宝田，李思贤

(北京交通大学，交通运输学院，北京 100044)

0 引言

数据采集设备的不断升级和交通流预测技术的快速发展，为获取可靠的交通流数据提供了保障[1]。在已知交通数据的情况下，如果能准确识别各交叉口的交通状态，并定量描述相邻交叉口在当前状态下的关联权重，就可以为信号控制方案的制定提供理论支撑，缓解交通拥堵。

现有研究热点主要集中在两个方面。一是交通状态识别方面，主要是从交通数据中提取交通状态的特征向量，利用人工智能算法建立交通状态识别模型。成卫等[2]利用浮动车的速度波动特征，以平均速度、对比度、逆方差这3 个特征指标建立基于多维高斯隐马尔可夫模型的道路交通状态识别模型，其效果优于支持向量机和随机森林模型；Wang 等[3]提出一种基于特征图和深度学习的交通状态识别模型，将交通状态特征向量转化为特征图，建立基于CoAtNet 算法的交通状态识别模型，并选取上海市车辆轨迹数据进行验证；朱秋圳等[4]利用轨迹速度—空间相似性将车辆队列连接为交通流簇，采用模糊C均值算法对路段上的交通状态进行识别。

二是相邻交叉口关联权重方面，Pang 等[5]提出高速公路相邻交叉口的耦合模型，建立基于密度的交通量转移方程，用于评价相邻交叉口的耦合强度；徐建闽等[6]提出一种基于Whitson 模型和交叉口饱和度的综合关联度模型作为控制子区划分的依据，并选择广州市实测数据进行验证；Ke 等[7]提出一种基于相邻交叉口之间距离和流量的关联度计算方法，并结合纽曼算法和自动车牌识别算法进行大规模路网下的子区划分实验，验证了其有效性；Hu等[8]从两个交叉口之间的流量、相位差、行程时间、排队长度、延误等5 个方面分别建立单独的关联度模型，并合并为综合关联度，作为主干路协调控制的依据，提高了干线路网的运行效率。

现有研究仍然存在一定的不足：(1)当前交通状态识别的研究对象多为路段上的交通流，其特征维度普遍较低，而在信号控制交叉口处，交通流会产生诸如排队长度、停车次数、流向比等新的特征参数；原有路段特征选取不能全面描述交叉口的交通状态，同时传统机器学习算法的性能随着特征维度和数据量的大幅增加而面临考验。(2)现有交叉口关联度模型中一些特定参数需要根据经验人工设置，如权重系数等，使模型本身存在主观性；此外，如车辆转移数、饱和度相异度等参数，均需要结合多种输入量进行计算，而且部分庞大的累加模型会随着某些数据误差不断偏离实际值，缺乏自我调整机制，影响关联度的可靠性。

路网是一种天然的图结构，而TGAT是近年来图神经网络领域重要的研究成果，一方面，它可以很好地将路网的拓扑结构、节点(交叉口)特征和连续时间函数进行聚合，具有较强的可解释性，能对任意时刻目标节点的状态进行动态划分，并且分类准确率普遍优于传统机器学习模型[9]；另一方面，它能应对多维度的输入数据，不需要额外输入人工参数，能在训练中不断调整邻居节点的权重系数，并且采用多头注意力机制，使整个模型有很强的表达能力。基于此，本文以VISSIM仿真数据为基础，将各交叉口的交通特征、交叉口的交互时间、交叉口的初始标签输入到TGAT模型中，输出目标交叉口在任意时刻的交通状态及其邻居交叉口关联度值，并与传统分类模型比较准确率。同时，选择两条主干路上共11 个交叉口的关联度值，从距离和流量两方面验证其有效性。

1 交通状态识别模型构建

基于TGAT 的交通状态识别模型与传统模型相比具有两方面优势：一方面它的运算性能受输入维度的限制较小，能适用于Reddit、Wikipedia、Industrial等多维度数据集，因此可以广泛选取交叉口的交通特征，全面描述交叉口的交通状态，使交通状态识别更准确；另一方面，TGAT 具有自注意力机制，可以将节点之间的自注意力值作为节点关联度，提高模型的可解释性，并且与GraphSage、GAT 等静态图相比[9]，它把时间信息映射到向量空间，可以更清晰地展现出节点在不同时刻对路网结构的影响，获得交叉口的动态关联度，为实时交通控制策略的制定奠定基础。

1.1 输入量的选取

基于TGAT的交叉口交通状态识别模型，其输入量包括交叉口特征矩阵F、交叉口交互时间矩阵T、交叉口初始标签矩阵L，输出量是目标交叉口在不同时刻的交通状态及其邻居交叉口的关联度。

(1)特征矩阵F

交叉口的特征可以分为交通流特征和物理特征，其中，交通流特征由车辆在运行过程中产生的交通数据组成，在VISSIM仿真环境中，通过节点检测器和数据采集点检测器可以得到交叉口各进口道的车辆总延误平均值(Dall)、每辆车的平均停车时间(Tstopd)、平均停车次数(Nstops)、通过车辆数(Nveh)、平均排队长度(Lqueue)；物理特征由交叉口自身的渠化和信号配时方案决定的，通过交通调查数据可以得到每个交叉口的信号周期时长(T)、各进口道直行方向有效绿灯时间(Tsg)、左转方向有效绿灯时间(Tlg)，并能根据流量流向比和交叉口的渠化方案得到各进口道的设计通行能力(C)。由于实验区域内交叉口的进口道数量均为3 或4，因此将每个交叉口的特征按照东、西、南、北这4个进口道进行设置，缺失方向的数据全部设置为0。因此一个交叉口东进口道的特征矩阵可表示为

则一个交叉口的特征F可表示为F=[fE,fW,fS,fN,T]，特征维度为33。

(2)交互时间矩阵T

在TGAT模型中，需要确定两个交叉口发生信息交互的时间t。为方便描述，假定有两个相邻交叉口，东侧为交叉口1，西侧为交叉口2。x时刻交叉口1东进口开始放行，之后南进口放行。放行车辆与交叉口2 各进行一次交互。第1 次交互为，交叉口1东进口的直行车流到达交叉口2；第2次交互为，交叉口1 南进口的左转车流到达交叉口2。两次交互所用的时间被设置为t1ES-2和t1SL-2。其中，ES 代表东进口道的直行方向，SL 代表南进口道的左转方向。由于车流在实际行驶过程中是离散的，很难形成一个统一的到达时间，因此选择该车流所在相位有效绿灯时间的中值作为全部车流的启动时间，再根据路段的距离和仿真中路段平均车速得到

式中：t1E_Sg为交叉口1东进口直行相位的有效绿灯时间；t1S_Lg为交叉口1南进口左转相位的有效绿灯时间；L1-2为交叉口间距；Vˉ1-2为平均速度。因此，交叉口1 和2 在时间矩阵T中的两次交互时间分别为[x+t1ES-2,x+t1E_Sg+ty+t1SL-2]，其中，ty为黄灯时间。

(3)标签矩阵L

采用文献[10]提出的快速搜索和发现密度峰值的聚类算法(Clustering by Fast Search and Find of Density Peaks,DPC)将特征矩阵F划分为4 类，并按照各类别中Lqueue的总量由小到大将这4 类数据的标签依次设置为畅行、平稳、拥挤、阻塞，作为数据的原始标签。

1.2 交叉口状态识别模型

将路网转化为图结构，其中交叉口对应路网节点，路段对应图中的边，交叉口的交通状态对应节点的状态标签，交叉口关联度对应邻居节点的权重。图1 是基于TGAT 的交叉口状态识别模型，共有l层，每一层都是一个局部聚合算子。每次训练从第一层TGAT开始逐层聚合节点信息，将上一层聚合后的节点信息和两层节点之间的时间差函数传入下一层，逐层进行，直到最后一层TGAT 聚合完毕，即完成一步训练过程。下面以第l层为例，介绍TGAT在每一层中聚合节点的过程。

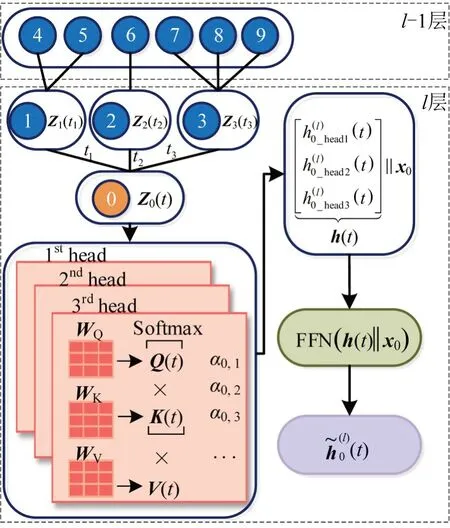
图1 TGAT层结构Fig.1 Structure of TGAT layer

第l层的节点关系描述：t时刻的目标节点0，分别在t之前的t1～t3时刻与其邻居节点1～节点3进行了1 次交互。节点1～节点3 分别与节点4～节点9在更早的时间之前进行过交互。

第l层的输入：第l-1 层的节点嵌入和时间特征。其中，节点嵌入表示tj时刻的节点i在第l-1 层中的节点嵌入；Φ(t-tj)为时间特征函数，表征节点之间的时间差。假定将时间映射到d维向量空间，则有

式中：ωm=[ω1,…,ωd] 为需要学习的参数。

需要特别说明的是，对于TGAT 的第一层，由于其没有上一层，所以时间特征函数为0，其输入仅为节点嵌入，该节点嵌入为交叉口特征矩阵F。

第l层的输出：目标节点0 在t时刻的节点嵌入

第l层中节点的聚合过程如下：

(1)寻找t时刻的目标节点0 的邻居节点。原TGAT中目标节点i的邻居节点集合为Ni，但选取过程仅考虑了时间差，对于交叉口而言，还应该考虑地理位置信息，否则有可能将距离极远的两个交叉口错判为邻居。文献[11]的研究表明，当间距超过1 km时，往往认为两交叉口不相关。因此，根据实际路网信息确定每个交叉口i的邻居备选集合Ri，则TGAT 中i节点的邻居节点集合Ntgat_i=Ni∩Ri，其中，Ri=[Ij|(Shortest Path＜1 km)]，表示第i个交叉口Ii在1 km距离内的邻居交叉口，距离以最短路为准。

(2)构造嵌入-时间特征矩阵。对于每个节点，将其在第l-1 层中的节点嵌入和时间特征函数进行拼接，组成嵌入-时间特征矩阵，即，由于0 节点和其自身的时间差为0，因此，。将上述所有矩阵进行拼接，则有

(3)将Z(t)用3 头自注意力机制进行聚合。即分别与查询向量WQ(Query)、键向量WK(Key)和值向量WV(Value)进行相乘。

用节点i和节点j之间的注意力权重αij代表节点之间的关联度，即

计算0节点聚合其邻居节点后的注意力值为

(4) 将得到的3 个注意力值合称为h(t)，并与x0进行拼接，其中，，是0 节点在第l-1层的节点嵌入。

(5) 经过FFN 全连接层，得到第l层的最终输出，即0 节点在t时刻的节点嵌入，并且得到0 节点的邻居节点对于它的影响权重矩阵α0_NBR=[α01,…,α0n]，其中，n为TGAT参数中邻居节点的个数。

(6)根据0 节点的节点嵌入值推断目标节点属于各类状态的概率，并结合初始标签矩阵L，计算交叉熵损失函数(CrossEntropyLoss)，误差反向传播更新模型参数，直到达到训练终止条件。

(7)将最后一次训练推断出的目标节点状态标签作为目标交叉口的最终交通状态，将此时的α0_NBR作为目标节点和其邻居节点的权重，即邻居交叉口关联度。

2 实例分析

选择北京市海淀区某区域路网2019 年某个工作日14:00-15:00的交通量调查数据进行研究，数据包括各交叉口进口道的分方向交通流量和交通信号周期。路网范围及交叉口编号如图2所示，其中信号控制交叉口33个。

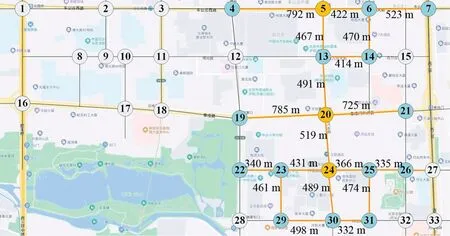
图2 路网范围及交叉口编号示意图Fig.2 Road network scope and intersection number diagram

2.1 相关参数设置

(1)VISSIM 中仿真最大时间为6300 s，数据获取时间为1800～6300 s，检测器的数据采集间隔为300 s，路网外围的各进口每1500 s按照其通行能力改变一次交通量，以模拟交叉口在不同时期的不同交通状态。

(2)本文设置2层TGAT模型，邻居节点个数为5，学习率为3e-4，丢弃率为0.15，，选择3 头注意力机制，迭代次数为500，优化器选择Adam。

(3) 设置3 种常用的分类算法进行对比试验。算法1 为GWO-MLP，即用灰狼算法(Grey Wolf Optimizatio,GWO)优化多层感知机(Multi-Layer Perceptron,MLP)，其中，GWO 的粒子位置信息设置为MLP中的初始权重和偏置量，种群数量为30，最大迭代数为300，MLP的隐含层数设置为2，隐含单元数设置为20，学习率为1e-3；算法2 为长短期记忆网络(Long short-term memory,LSTM)，网络框架为PyTorch，隐含层数设置为2，隐含单元数设置为32，丢弃率为0.15，学习率为3e-3；算法3 为支持向量机(Support Vector Machine,SVM)，核函数选择径向基核函数(Radial Basis Function,RBF)，选择10 折交叉验证寻找最优的RBF 参数g和惩罚因子C。

2.2 交叉口状态识别结果

在仿真时间段内，各交叉口共进行4933 次交互，即样本总量。训练集、验证集、测试集的划分比例为[0.70,0.15,0.15]，计算4种算法测试集的准确率(Accuracy)、精确率(Precision)、召回率(Recall)、F1度量(F1-score)，结果如图3所示，图3中各参数为宏平均值(Macro-average)。

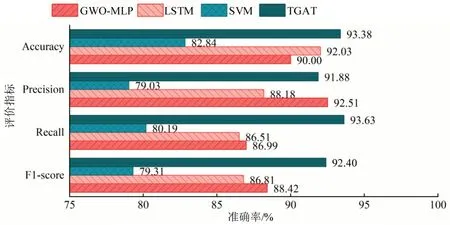
图3 各算法评估指标Fig.3 Evaluation index of each algorithm

从图3 可以看出，TGAT 模型的4 项指标全面优于其他算法，均在91%以上，尤其对于相对数据偏低的召回率，其领先幅度较大，说明各类中预测对的正样本在整个真实正样本中占比较高。LSTM的效果和GWO-MLP比较接近，每一项指标的差距都在4%以下，而SVM的效果相对最差。由于样本划分是按照时间顺序进行的，在仿真实验后期，路网中的车流不断累计，交叉口多处于拥挤状态，因此测试集中标签3 的数量较多，标签1 和4 的数量相对较少。测试集中畅行、平稳、拥挤和阻塞标签的数量分别为[146,139,372,83] 。传统模型在这种标签分布不均匀的情况下表现较差，例如GWOMPL的畅行标签、LSTM的阻塞标签、SVM的阻塞标签，单类的分类准确率都不到60%，而TGAT 对于各类标签的准确率均在86%以上。

2.3 交叉口关联度结果可视化

目标节点嵌入的维度和TGAT 的输入量特征矩阵F的维度一致，维度较大，采用文献[12]提出的t-SNE (t-Distributed Stochastic Neighbor Embedding)算法进行降维，降维结果如图4所示。

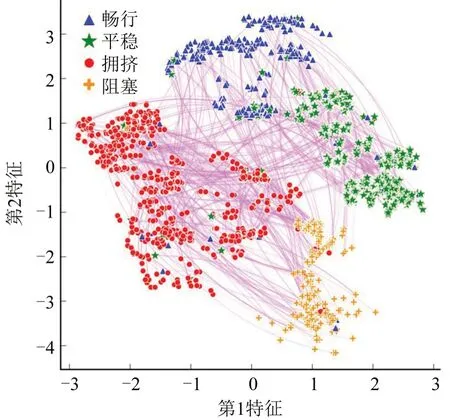
图4 节点嵌入t-SNE的可视化结果Fig.4 t-SNE visualization results of node embedding

由于数据量过大，且仿真初期路网的车流量较小，交叉口状态标签的分布不均衡，因此选择每个交叉口的第30～60条交互信息进行展示，降维的数据为第2层TGAT在最后一次迭代中的目标节点及其邻居节点的节点嵌入值。图4 中不同形状的点对应不同的标签，线条的粗细代表节点间权重的大小。可以看出，所有点被大致分为了4 个簇，簇之间界限较为清晰，表明TGAT不仅可以对目标交叉口在不同时刻的交通状态进行识别，还可以定量描述其与邻居交叉口的关联度值，模型具有较强的可解释性。

2.4 交叉口关联度有效性检验

车流量是评判交叉口状态的重要参数。在所有汇入目标交叉口i的车流量中，若某一方向的流量占比最大，则通常情况下认为该方向对应的邻居交叉口最重要。如果流量占比和关联度的大小相近，则可以认为得出的关联度相对可靠。为了验证邻居交叉口权重α的可靠性，假设目标交叉口i的最近邻居交叉口为Ntgat_i=[I1,I2,…,In]，各邻居对应的权重为α=[α1,α2,…,αn]，权重最大的交叉口为Imax，对应的权重为。设置权重评判系数ω，其计算公式为

式中：qj为交叉口Ij流向i的非右转车流量；qS为Imax流向i的直行车流量；qL为Imax流向i的左转车流量；为Imax流向i的非右转车流量在所有流向i的非右转车流量中的占比；β为调整系数，本文取1.2。根据上述定义，当ω取值接近于1时，表示αi相对准确。需要说明的是，由于TGAT中考虑了时间对节点交互的影响，在Ntgat_i中，同一个交叉口可能出现多次，因此需要计算。下面以交叉口5、20、24为例进行说明，如图5所示。

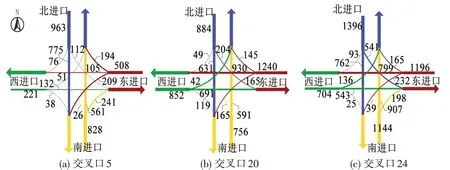
图5 交叉口5、20、24流量流向图Fig.5 Flow direction diagram of intersection 5,20 and 24

图5 为VISSIM 中交叉口5、20、24 的数据采集点检测器在仿真中第3300～3600 s的交通量流量折算为1 h 交通流量的流向图。根据TGAT 模型，得到3447 时刻的交叉口5、3570 时刻的交叉口20、3556时刻的交叉口24最近的5个邻居节点分别为

其最近邻居分别为3372 时刻的交叉口13(权重0.443)，3547时刻的交叉口13(权重0.403)和3502时刻的交叉口20(权重0.552)，由式(8)可计算得出ω的值依次为1.089、1.375、1.094。

文献[5-8]的研究结果均表明，两交叉口之间一种有效的关联度和他们的间距是相关的。为了进一步验证TGAT中关联度与距离的关系，按照邻居交叉口到上述3 个交叉口的距离(如图2 所示)，以500 m和800 m作为分界线把所有邻居交叉口分成3 组。第1 组为500 m 以内的邻居交叉口，包括交叉口6、13、23、25、30；第2 组为500～800 m 的邻居交叉口，包括交叉口4、19、20、21、22、24、26；第3组为800～1000 m 的邻居交叉口，包括交叉口5、7、14、23、25、29、31。以100 s为单位计算训练集时间(1800～4500 s)内3 组邻居节点的平均权重，其拟合曲线如图6 所示，图中阴影部分的上下限为5 次实验的极值。

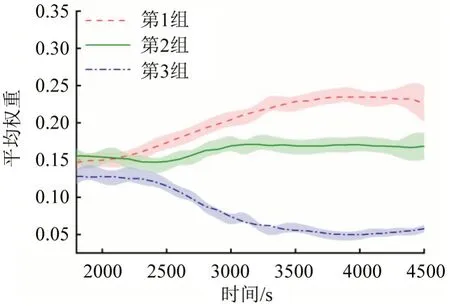
图6 不同节点的平均权重拟合曲线Fig.6 Average weight fitting curve of different nodes

根据1.1 节的定义，交叉口进行交互的次数与距离、信号配时方案和路段平均车速有关。通常情况下，距离越近交互次数越多。从图6 可以看出：随着仿真时间的增加，第1 组6 个交叉口的平均权重不断增加，在3800～3900 s 区间内总占比达到最高，为47.89%，第2组增长平稳，第3组距离较远的交叉口平均权重越来越小。结果表明，TGAT 更关注与目标节点距离较近且交互次数较多的重要邻居节点，其分配的权重与距离负相关。

为了进一步验证，选择路网中两条主干路(车公庄西路和展览馆路)上的11 个交叉口进行研究，交叉口编号为1～7、13、20、24、30，对他们的权重评判系数ω进行统计，箱型图如图7所示。

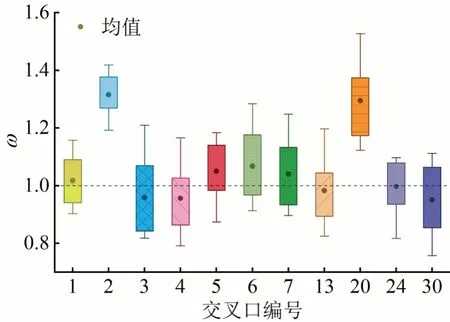
图7 部分交叉口权重评判系数箱型图Fig.7 Box diagram of weight evaluation coefficient of some intersections

从图7 可以看出，除交叉口2 和交叉口20 之外，其余交叉口的权重评判系数均值都在1 左右，表明这些交叉口的关联度与车流量密切相关，其中交叉口1、4、5、13、24的箱体长度较短，数据波动范围很小，权重评判系数比较稳定，而交叉口2 和交叉口20的均值明显偏高。

交叉口2的东—西方向为主干路，南—北方向为单车道道路，两个方向的车流量差距在4 倍以上，而交叉口2 与9、10、11 交叉口的相对距离又较近，发生交互的频率很高，这会导致权重较大的邻居交叉口对于交叉口2的实际的流量贡献很低，导致ω普遍偏大。交叉口20 存在类似的问题，主要原因是其与邻居交叉口的相对距离普遍较远，最近的4 个邻居交叉口(13、19、22、24)距离均在491 m以上，位置较为孤立，交互次数较少，所以ω的波动范围偏大，并且南—北方向的邻居节点距离相对较近，对应的流量相对偏少，同样会导致ω的均值偏大。由此可见，ω适用于大多数主干路上流量分布相对比较均匀的非孤立交叉口，可以用来评判关联度的有效性，关联度与流量正相关。

3 结论

基于仿真数据提取交叉口交通特征，提出基于TGAT 的交叉口交通状态识别模型，可以同时得到交叉口的交通状态和邻居交叉口关联度，对分类准确率和关联度的有效性进行了验证，得出结论如下：

(1)通过建立33 维的交叉口交通特征矩阵，定义交叉口交互时间，并根据实际路网结构优化邻居交叉口的选取规则，可以将交叉口状态识别问题转化为图神经网络中节点的分类问题，结合注意力机制可以得到交叉口的动态关联度。

(2)基于TGAT 的交叉口交通状态识别模型在分类准确率、精确率、召回率、F1 度量等多项指标上均高于GWO-MLP、LSTM、SVM 这3 种分类模型，并且对于标签分布不均匀的样本，每一类的准确率都高于86%，具有较好的分类效果，可以准确识别交叉口在不同时刻的交通状态。

(3)本文得出的交叉口关联度与邻居交叉口的流量正相关，与距离负相关。选取的11 个主干路交叉口中，有9 个交叉口的结果表明，邻居交叉口关联度较大，其流量在目标交叉口总流量中的占比也较高。另外2个交叉口的结果表明，较短的交叉口间距意味着更多的交互次数，即它们的流量贡献较小，但是TGAT仍然会逐步增加对这类交叉口的关注度，提高其相对权重，与理论分析一致，关联度具有有效性和可解释性。

本文还存在一些不足：一方面，需要从更大的路网范围验证交通状态识别的准确性和关联度的有效性；另一方面，关联度还应该带入到后续控制子区划分算法中验证其具体应用价值。