一道课本习题的多解、推广与应用
顾美娟
(江苏省启东市东南中学,江苏 启东 226200)
课本是教学之根本,也是考题之源头.很多高考题和竞赛题都源自课本习题的改编或者延伸,因此,深度探究课本习题对教学及其考试备考来说是非常重要的.
1 课本习题
题目(2019年人教A版《数学必修第二册》[1]53页第15题)△ABC的三边分别为a,b,c,BC,CA,AB边上的中线分别记为ma,mb,mc,利用余弦定理证明
2 解法探究
证法1 如图1,对△ABD利用余弦定理,得

同理, 可得mb,mc.
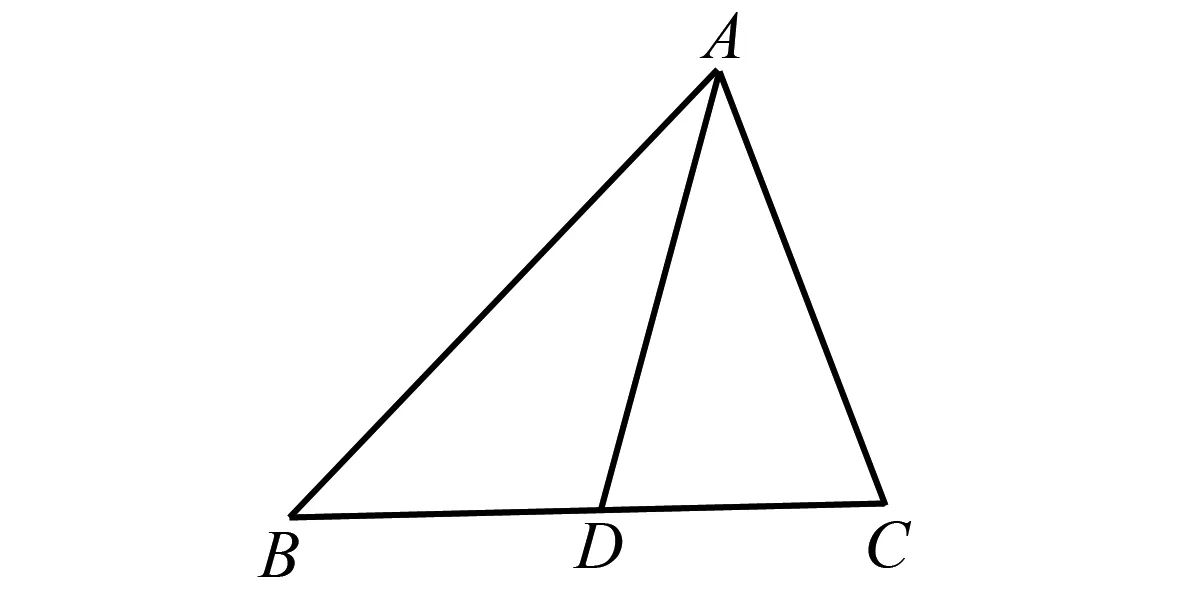
图1 三角形及其中线
证法2 如图1,对△ADB和△ADC利用余弦定理,得cos∠ADB+cos∠ADC=0.

即2AD2+2DB2-AB2-AC2=0.



同理可得mb,mc.
证法3 无论是锐角三角形(图2)还是钝角三角形(图3),都有
AB2=AH2+(BH)2=AD2-DH2+(BD+DH)2=AD2+BD2+2BD·DH,
AC2=AH2+CH2=AD2-DH2+(DH-DC)2=AD2+DC2-2DC·DH.
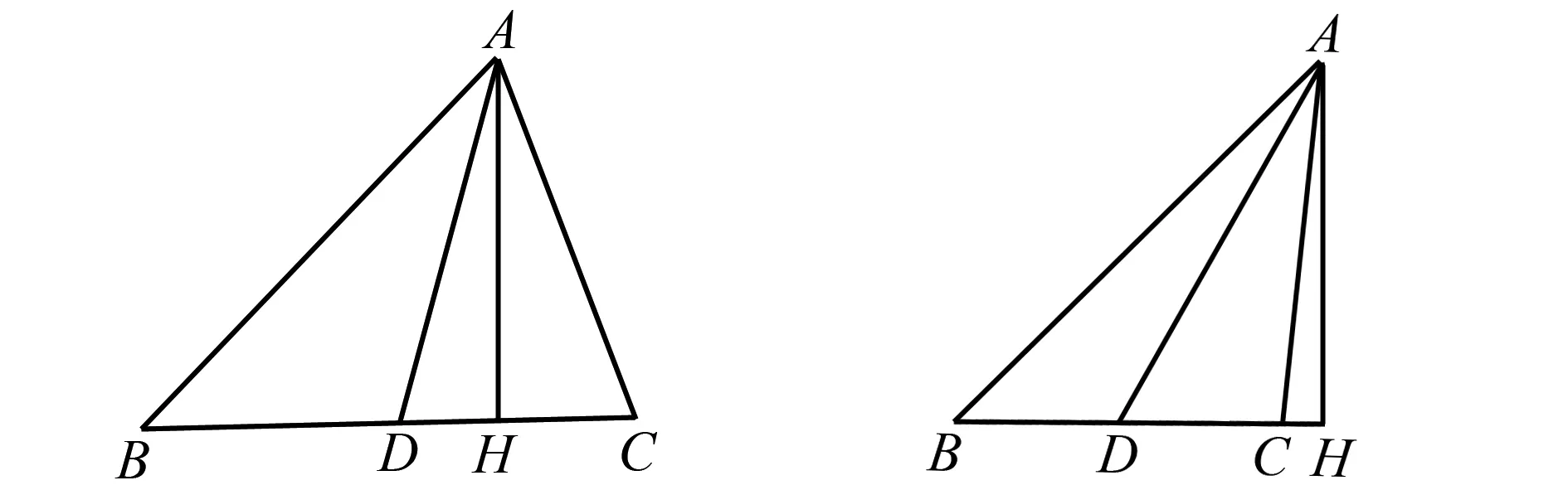
图2 锐角三角形 图3 钝角三角形
两式相加,得
AB2+AC2=2(AD2+BD2).


同理可得mb,mc.
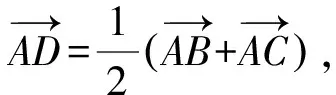


同理可得mb,mc.



同理可得mb,mc.
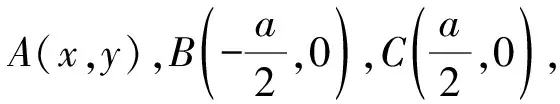
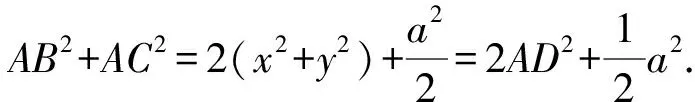


图4 建立坐标系
3 习题推广
设△ABC的三边分别为a,b,c,BC,CA,AB边上的中线分别记为ma,mb,mc. 经过探究,得到如下的结论.



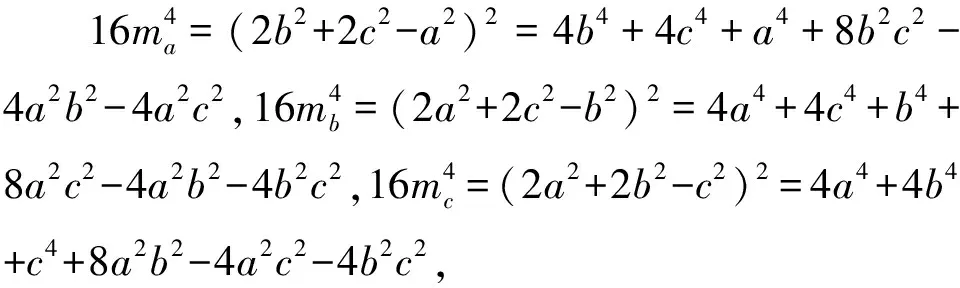
命题3ma=mb⟺a=b.

命题4△ABC是等边三角形⟺ma=mb=mc.
证明由命题3可知,△ABC是等边三角形⟺a=b=c⟺ma=mb=mc.
命题5 设△ABC的面积和半周长分别为S,p,则mambmc≥pS.
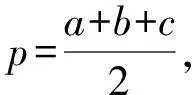
≥p(p-a).


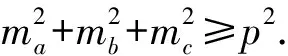


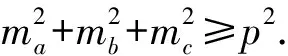

证明由中线公式与余弦定理,得
=b2+c2+2bccosA



三式相加,即得证.
4 在竞赛中的应用
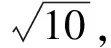
解析记M为AC的中点,由中线公式得
4BM2+AC2=2(AB2+BC2).

由余弦定理,得
于是

通过一道课本习题的证明,复习巩固了解三角形常用的方法,即余弦定理、勾股定理、向量法和坐标法. 进一步,我们利用课本习题的结论(即中线公式)可以得到很多漂亮的结论,也可以解决竞赛中的一些问题.

