因对称而精彩 因和谐而美丽——例谈以弹簧振子运动模型为载体的问题分析策略

许冬保

(江西省九江市第一中学,江西 九江 332000)

赵凯华先生在《新概念物理教程·力学》[1]中指出:“人们习惯于按照物质运动的形态,把物理学分成力(包括声)、热、电、光等子学科.然而,某些形式的运动是横跨所有这些学科的,其中最典型的要算振动和波了.”基于此,在老高考(选考+必考)命题中,必考试题中涉及振动模型的问题就很正常了,新高考中振动和波(全国卷及部分自主命题省市)属于必考内容.文章兼顾新老高考复习,基于物理观念的视角对弹簧振子简谐运动模型的应用作些分析,期望为考生备考提供助益.

1 弹簧振子运动模型的建构与表征

众知,凡一个物体受到跟相对平衡位置的位移成正比,方向与位移相反的回复力作用下的振动,叫做简谐运动.简谐运动是一种最基本、最简单的运动.

1.1 模型建构

如图1,轻弹簧与小球连接的系统构成弹簧振子.弹簧左端固定,小球穿过水平光滑杆.当小球位于O点时(平衡位置),弹簧弹力F为零.若使小球偏离O一段距离x,由静止释放小球,则小球受力F作用,在O点附近(B、C间)持续地振动起来.选O为坐标原点,以向右为正方向,则有

F=-kx

显然,弹簧振子的振动是简谐运动.

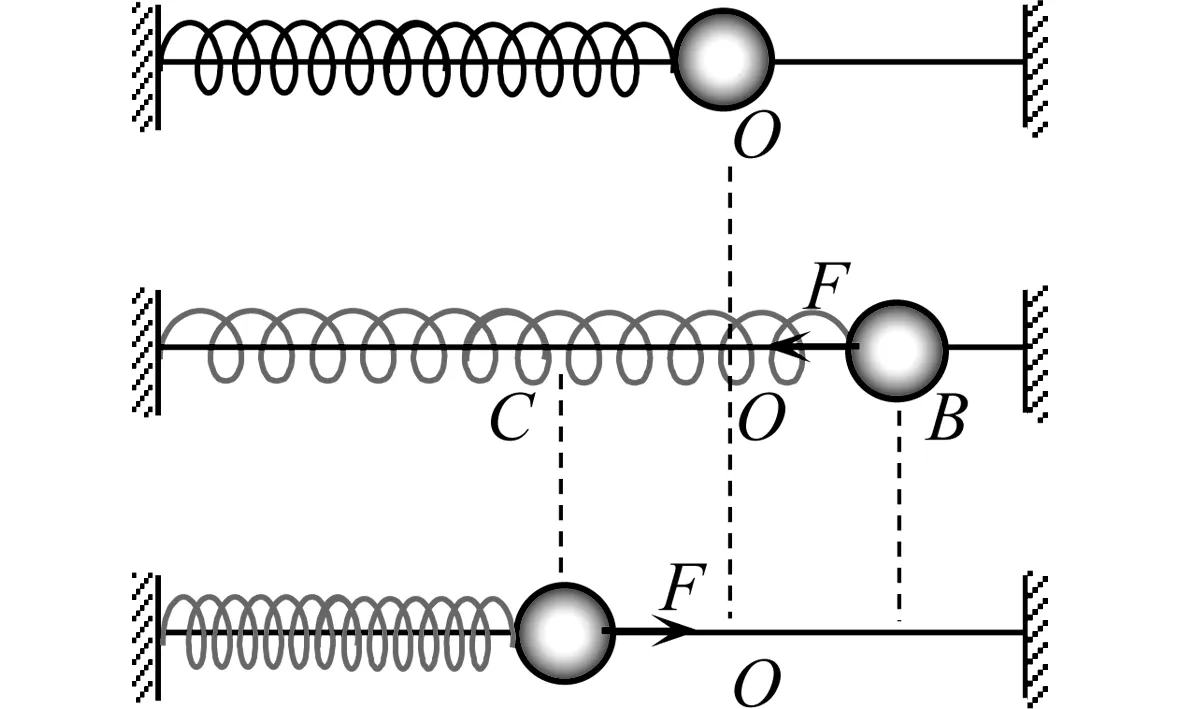
图1 弹簧振子的简谐运动模型

1.2 运动方程

理论表明:匀速圆周运动的投影运动是简谐运动.在如图2所示的参考圆中,质点P沿逆时针方向做匀速圆周运动,则P在x轴上的投影运动即为简谐运动.可以方便地得到以下规律.

小球离开平衡位置的位移x随时间t变化规律为

x=Acos(ωt+φ0)

式中,A、ω、φ0分别表示振幅、圆频率与初相,且为常量.

图2 参考圆分析简谐运动

P的速度及加速度在x轴上的分量分别为

v=-Aωsin(ωt+φ0);a=-Aω2cos(ωt+φ0) .

x、v、a对应的表达式,分别表示简谐运动的位移方程、速度方程及加速度方程.

1.3 运动周期

由描述x、a的方程知a=-xω2.结合牛顿第二定律,有F=-xmω2

该式与F=-kx相比较,有k=mω2.可得振动的周期公式

1.4 运动能量

不计任何能量损耗,弹簧振子的振动是简谐运动,振动系统的机械能守恒.因此,某时刻振动系统的总能量为

2 应用分析

如上所述,弹簧振子的振动是简谐运动,其x、v、a等物理量均随时间t按正弦或余弦规律变化,并且对平衡位置具有时空对称性,对称性特征彰显振动的美丽与和谐.以弹簧振子简谐运动为载体的物理问题,可以由运动观念、能量观念、动量观念、图像观念等视角进行分析.

2.1 运动观念分析

(1)h的大小;

(2)0.6 s内物块运动的路程;

(3)由位移y的振动方程,写出相应的速度及加速度随时间变化的关系式.

图3 振动与落体运动模型

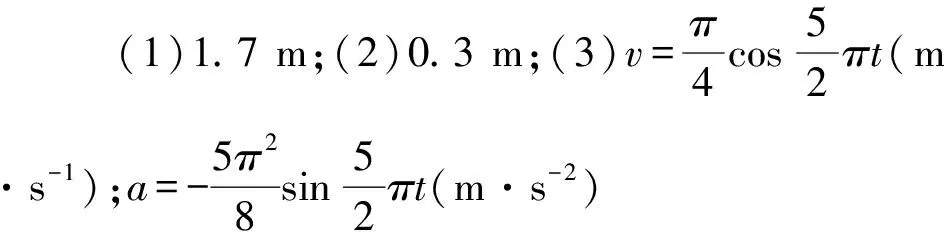
2.2 能量观念分析

例2水平面上有一弹簧振子,不计弹簧质量及任何阻力,振子作振幅为A的简谐运动.若小球在O点的速度为v0,振动中某点P到O点的位移为x.试求

(1)振子在P点的速度v及振动的周期;

(2)定性画出v随x变化的函数图像.

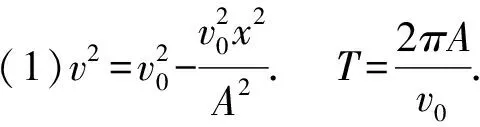
2.3 动量观念分析

例3如图5,倾角θ=30°足够长的光滑斜面固定在水平面上,两个物体A、B通过细绳及轻弹簧连接于光滑轻滑轮两侧,B的质量为m,开始时用手按住物体A,物体B静止于地面,滑轮两边的细绳恰好伸直,且弹簧处于原长状态.松开手后,当B刚要离开地面时,A恰达最大速度v,空气阻力不计.

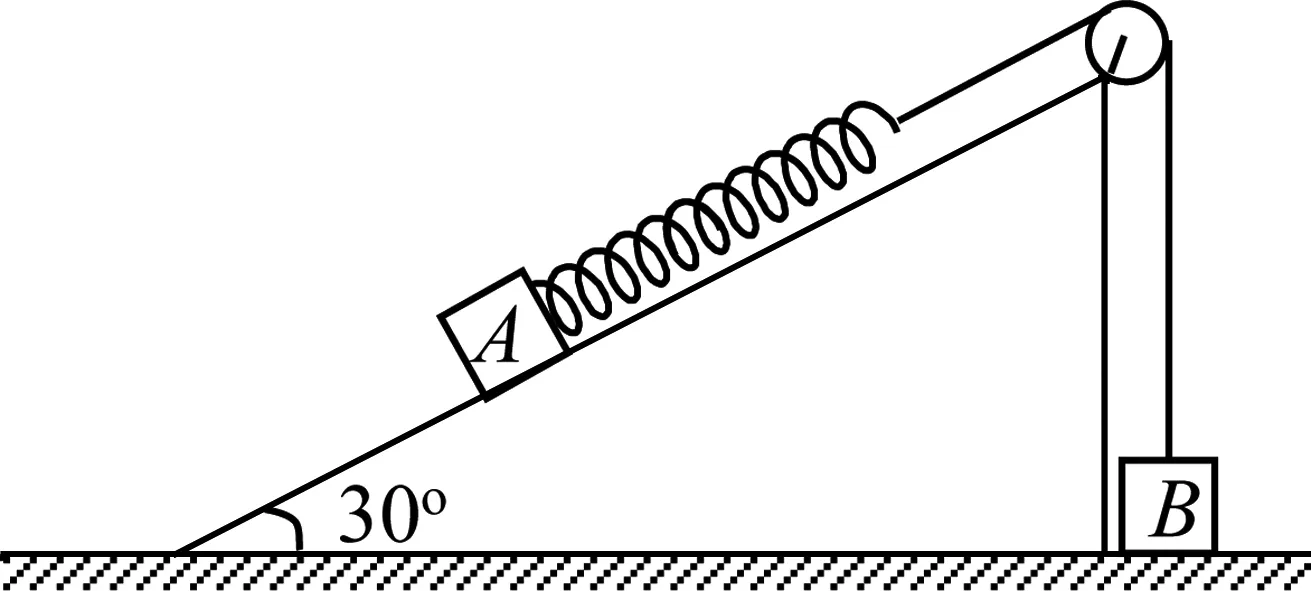
图5 斜面上的振动问题

(1)求A的质量M;

(2)A下滑过程中弹簧最长时,A的速度v1为多少?

2.4 图像观念分析

例4如图6,某轻质弹簧劲度系数为k,弹簧下端固定在地面,上端固定连接一个轻质的小托架.质量为m的小球从离托架一定高度处由静止开始自由下落,小球恰好落到托架中心位置,然后经过一段时间又回到初始下落位置.弹簧始终在弹性范围内,不计空气阻力.

图6 竖直方向的振动问题

(1)若小球运动到O点时速度最大,则以O点为位移起点(小球在任意位置P的位移为OP),设竖直向下为正方向,作出小球在上述运动过程中的加速度a随位移x变化的a-x图像(特殊点需要标出坐标)﹔

(2)若小球在上述运动过程中的最大加速度为2g,利用a-x图像,求小球初始下落位置距小托架的高度.

答案(1)

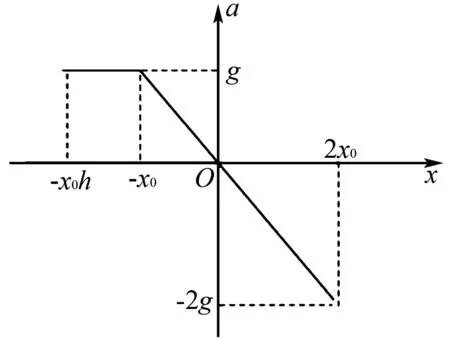
图7 小球运动的a-x图像

物理观念是从物理学视角形成的关于物质、运动与相互作用、能量等的基本认识,是解决实际问题的基础[2].在某一个具体问题的分析中,所涉及到的物理观念其实并非单一,文中的分类是基于问题解决的核心观念出发的.

由于受传统考试大纲的局限,弹簧弹性势能的表达式并不作为考查的内容,因此在实际教学中,往往回避.若将弹簧弹性势能的表达式作为科学探究的内容,在核心素养理念下,从线性力做功的角度(例2评述)或通过图像等手段均可导出弹簧弹性势能表达式,这有利于学生从能量观念的视角深度理解弹簧的本质.另外,在当今高校强基测试中,明确要求能够掌握弹簧弹性势能的表达式并能进行相关的计算.因此,在教学中建议将弹簧弹性势能表达式列为教学目标的内容.