利用费马原理 求解最值问题
王伟民
(安徽省太和县宫集镇中心学校,安徽 太和 236652)
满足什么条件“时间最短”“做功最少”“造价最低”等问题是物理研究和生活中常见的最值问题.而费马原理说的是光在介质中两确定点之间传播时,总是沿光程(即时间)最短的路径传播,涉及到“时间最短”问题.如果对光的折射规律进一步推广,还可以推理出与行程问题有关的其他量存在最值的条件[1].所以,利用费马原理可以比较方便地解决一些相关的确定一些量最值的实际问题.
1 利用费马原理证明光的折射定律
利用费马原理,很容易证明“在同种均匀介质中光沿直线传播”、光在反射时“反射角等于入射角”等光学规律.光在两种介质分界面发生折射时,折射角与入射角间的定量关系:“折射角与入射角正弦之比等于光在两种介质中传播速度之比”这一规律,也可以通过费马原理进行逻辑推导.
如图1所示,设l是两种介质的分界面,A、O分别是两种介质中的两定点,一条光线由A点发出,经界面B点折射后传播至O点.以O为坐标原点,平行于分界面的方向为x轴建立平面直角坐标系,设A点坐标为A(a,b),光在两种介质中的传播速度分别是v1和v2,入射角和折射角分别是α和β,若O点到分界面的竖直距离为h(h 图1 光在两种介质中折射示意图 图2 落水及施救人员初始位置图示 由图可知,光从A点出发经B传播到O需要的时间为: 为确定时间的最小值,将时间t对x求导可得: 令t′=0可得: 实际上,我们上面利用费马原理推导光的折射定律的推理过程中,得出的等式(1)是一个关于B点横坐标x的一元方程,而实际问题需要在某个变化过程中求相关量的最大值或最小值时,往往需要确定类似光的折射问题中折射点位置的其他相关问题中“转折点”的位置,所以,确定方程(1)的解就显得尤为重要. 例1 如图2所示,一幼童不慎落入河水中的B点,岸上的人员在A处闻讯后,迅速跑步前去救援,已知救援人员得到信息时距离河岸30 m,落水者距离河岸24 m,二人水平距离为47 m,若救援人员在岸上跑步的最大速度和水中游泳的最大速度分别是8 m/s和2.8 m/s,问救援人员最短在多长时间内可以到达落水幼童处?(结果保留分数) 解析救援人员有无数种救援路径可以选择,最容易想到的是图3所示的几种情形,由以上分析可知,这些都不是救援人员按最大速度到达落水幼童位置时间最短的行走路线,救援人员行走和游泳总时间最短的路径应该满足费马原理,即光的折射规律[2]. 图3 几种常见施救路径图示 图4 相关角度和距离图示 例2如图5所示,A、B两城之间有一块宽度为24 km的矩形沼泽地,两城到沼泽地边缘的垂直距离分别是18 km和6 km,两城在平行于沼泽地边缘方向上的距离是39 km.现欲在两城市之间修建一条高速公路.经测算陆地上公路的造价是0.7亿元/公里,沼泽地上公路造价是2亿元/公里,请设计公路的走向,使总造价最低,并求出最低总造价. 图5 两城之间地况数据图示 图6 两城之间修建公路示意图 解得:x=8 因此,整个工程的最小总造价为P最小=s陆地a陆地+s沼泽地a沼泽地=40×0.7+25×20亿元=78亿元 答:修建公路的最低总造价为78亿元. 由上面的这些例子可以看出,费马原理不仅可以解决行程问题中特定情况下时间的最小值,也可以解决与行程问题类似的其他跟路程相关的有关量的最值[4].



2 费马原理在行程问题确定时间最值时的应用
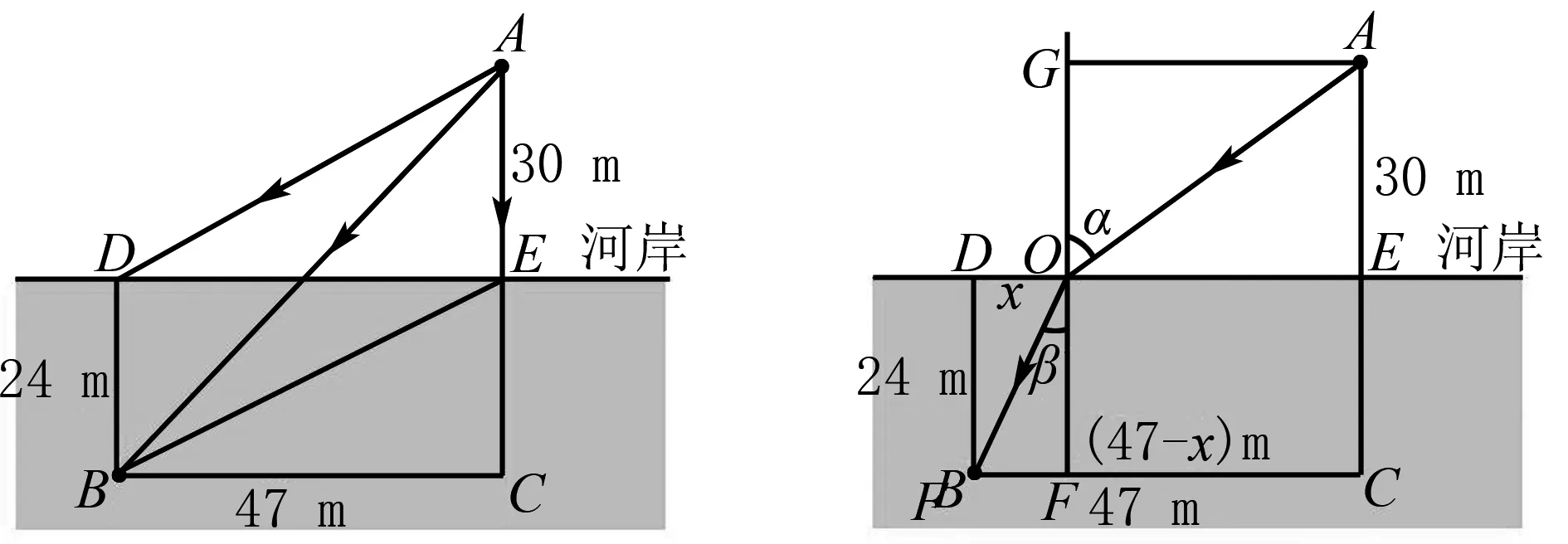

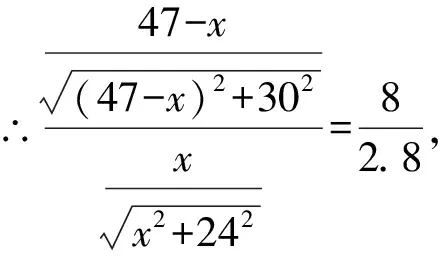
3 费马原理在其它问题确定最值时的应用






