立足基本图形 培养直观想象素养
——以2023年高考全国卷立体几何试题为例
姚振晖
(福建省永春美岭中学,福建 泉州 362619)
直观想象是发现和提出数学问题、分析和解决数学问题的重要手段[1]. 直观想象要求考生能够借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,构建数学问题的直观模型,探索解决问题的思路[2]. 高考数学中直观想象素养的考查要求为:能根据条件画出正确的图形,根据图形想象出直观形象;能正确分析图形中的基本元素及其相互关系;能对图形进行分解、组合;会运用图形等手段形象地揭示问题的本质[3].
1 正方体模型
例1(2023年全国甲卷理科15题)在正方体ABCD-A1B1C1D1中,E,F分别为CD,A1B1的中点,则以EF为直径的球面与正方体每条棱的交点总数为____.
解析不妨设正方体棱长为2,EF中点为O,取AB,BB1中点G,M,侧面BB1C1C的中心为N,连接FG,EG,OM,ON,MN,如图1所示.

图1 正方体

同理,根据正方体的对称性知,其余各棱和球面也只有1个交点,所以以EF为直径的球面与正方体每条棱的交点总数为12.
评析通过直观想象与简单的数学运算,可以确定以EF为直径的球的球心O也是正方体ABCD-A1B1C1D1的中心O,所以,点O到各棱的距离均等于OE,因此以EF为直径的球的球面与正方体的棱共有12个公共点.
2 三棱锥模型

(1)证明:EF∥平面ADO;
(2)证明:平面ADO⊥平面BEF;
(3)求二面角D-AO-C的正弦值.
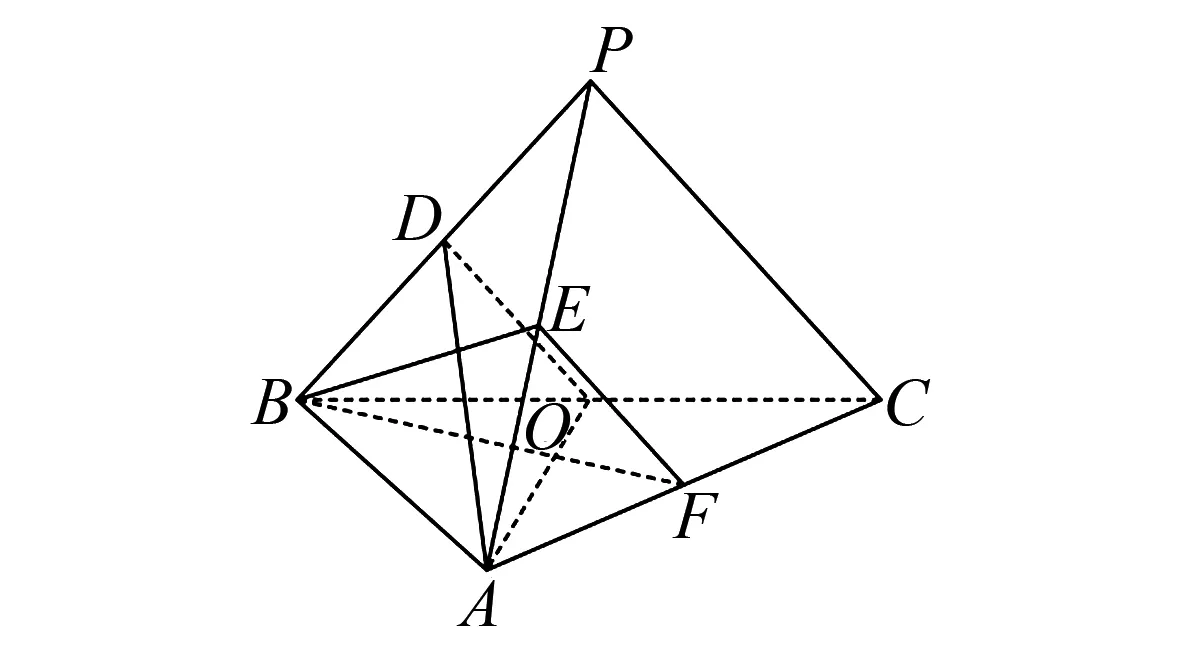
图2 例2示意图
评析先通过解三角形确定F为AC的中点,利用中位线的性质得到EF∥PC∥DO,再根据线面平行的判定定理可以得出第(1)问的结论. 第(2)问通过图形判断要证明的核心结论是AO⊥平面BEF,所以要在平面BEF中找到两条相交直线和AO垂直,结论的证明为第(3)问建立空间直角坐标系做铺垫.
3 圆锥模型
例3(2023年新课标Ⅱ卷第9题)已知圆锥的顶点为P,底面圆心为O,AB为底面直径,∠APB=120°,PA=2,点C在底面圆周上,且二面角P-AC-O为45°,则( ).
A.该圆锥的体积为π

评析本题以多选题的形式全面考查了圆锥的内容. 如图3所示,通过二面角P-AC-O为45°可以确定点C在底面圆周上的位置. 再根据圆锥的母线长为2,可以得到圆锥的底面圆半径和高,为后面的计算奠定基础.题目的四个选项设问逐次递进,前面的选项为后面的选项提供条件.

图3 圆锥
4 三棱柱的外接球模型
例4(2023年乙卷文科第16题)已知点S,A,B,C均在半径为2的球面上,△ABC是边长为3的等边三角形,SA⊥平面ABC,则SA=____.


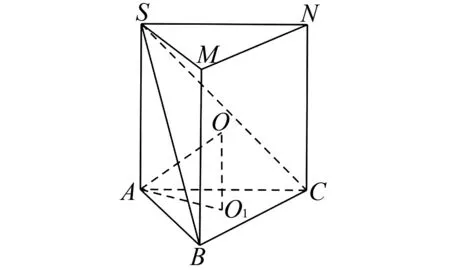
图4 三棱柱
评析本题虽然是考查三棱锥的外接球问题,但由于SA⊥平面ABC,所以可把三棱锥S-ABC放到三棱柱SMN-ABC中,这样,就将三棱锥的外接球转化为了三棱柱的外接球. 因为三棱锥的外接球形式多样,但三棱柱的外接球模型比较简单,如图4,易知三棱柱的外接球的球心O就是两个底面三角形外接圆圆心的中心,而AO1就是△ABC外接圆的半径,利用正弦定理可轻松得到.
5 正方体的内切球模型
例5(2023年新课标Ⅰ卷第12题)下列物体中,能够被整体放入棱长为1(单位:m)的正方体容器(容器壁厚度忽略不计)内的有( ).
A.直径为0.99 m的球体
B.所有棱长均为1.4 m的四面体
C.底面直径为0.01 m,高为1.8 m的圆柱体
D.底面直径为1.2 m,高为0.01 m的圆柱体
解析对于选项A,如图5,因为正方体的内切球(与各个面都相切)的直径为1,且1>0.99,所以A正确.


图5 正方体内切球 图6 正四面体放入正方体内


图7 正方体内放不下圆柱

图8 正方体的截面 图9 正六边形
评析以正方体的内接几何体(包括球、正四面体、圆柱等)为情境,考查正方体的棱长、面对角线的长和体对角线的长的关系等. 结合组合体的位置关系,利用空间问题平面化,通过分析选项中各个几何体与正方体的棱长、面对角线和体对角线长的数量关系迅速找到破解此题的切入点.
纵观2023年高考全国卷的立体几何试题,基本上都是以基本图形为模型,考查线面关系、外接球、内切球以及截面问题. 这些试题在考查数学运算核心素养和逻辑推理核心素养的同时,更全面考查了考生的直观想象核心素养. 平时要注意积累一些常见几何体的内切和外接模型,以及熟悉空间几何体的截面问题.

