强基计划数学备考系列讲座(18)——三角函数与三角变换

王慧兴(正高级教师 特级教师)

(清华大学附属中学)

1 知识与技能

1.1 知识主线

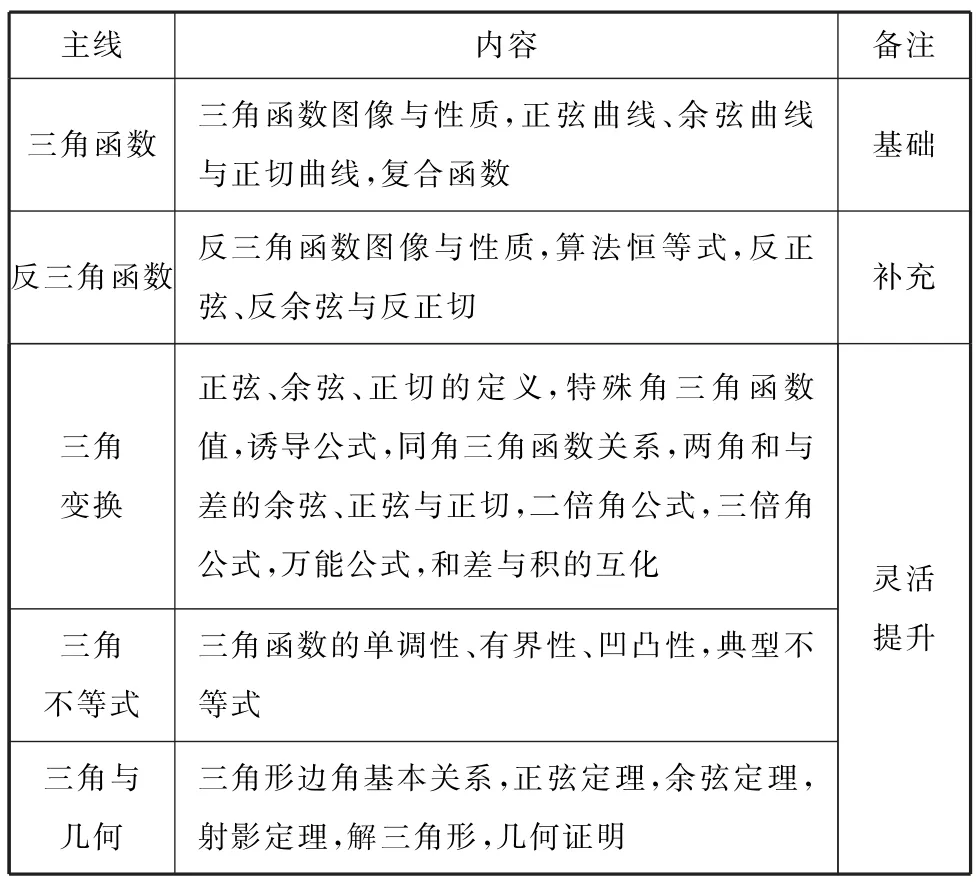
表1

1.2 要点解析

1)典型不等式

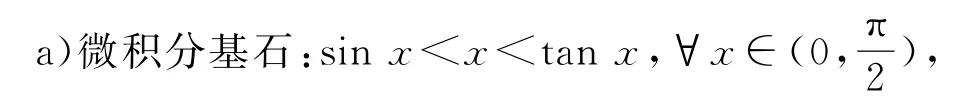
证明

所以嵌入不等式得证,其中等号成立的条件是

2)公式拓展

a)三倍角公式:

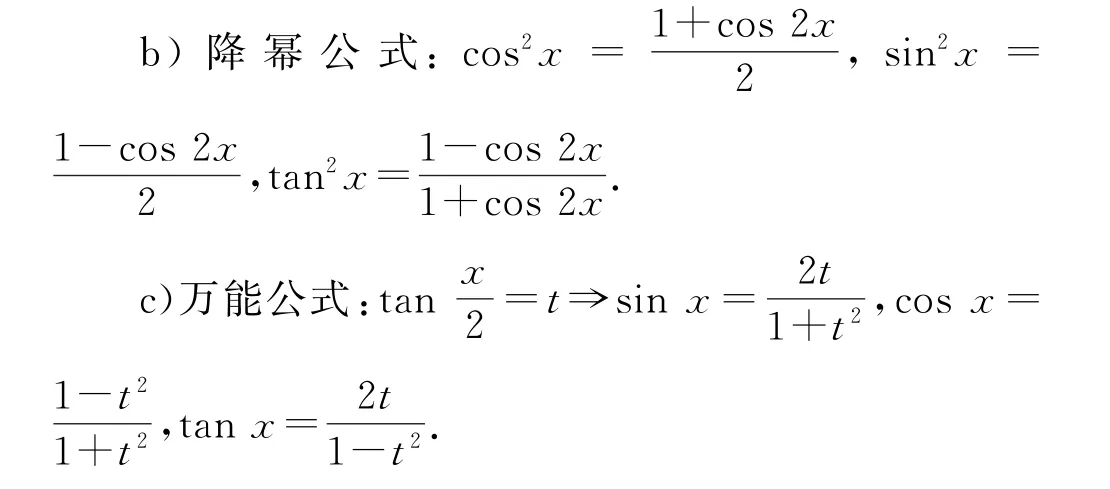
3)反三角函数的概念与算法

反三角函数是现行高中数学教学弱化的内容,但笔者梳理高校强基计划数学笔试试题发现,反三角函数运算题仍时有出现,因此强基应试复习务必扎实掌握反三角函数的概念与算法.

a)基本概念.

函数y＝sinx存在反函数,称为反正弦函数,记作y＝arcsinx,x∈[－1,1].算法恒等式有

注意sin(arcsinx)有意义的条件是x∈[－1,1],而arcsin(sinx)对x∈R 都有意义.

函数y＝cosx,x∈[0,π]存在反函数,称为反余弦函数,记作y＝arccosx,x∈[－1,1].算法恒等式有

注意cos(arccosx)有意义的条件是x∈[－1,1],而arccos(cosx)对x∈R都有意义.

函数y＝tanx,存在反函数,称为反正切函数,记作y＝arctanx,x∈R.算法恒等式有

b)基本运算.

反三角函数的三角运算:

三角函数的反三角运算:

4)三角与几何

a)三角形边角关系.

非直角三角形常用恒等式:

tanA＋tanB＋tanC＝tanAtanBtanC.

在△ABC中,A＞B⇔a＞b⇔sinA＞sinB.

在锐角△ABC中,若A≤B≤C,则

根据三角变换及均值不等式,可以建立三角恒等式与三角不等式,例如:

b)塞瓦定理角元形式.

塞瓦定理:在△ABC内部任取一点P,都有

当点P位于△ABC外部时,如果把等式中各角理解为有向角,则等式仍然成立.

证明 如图1所示,由面积关系公式得

三式相乘即可.

如图2所示,同理可证得当点P位于△ABC外部时,等式成立.

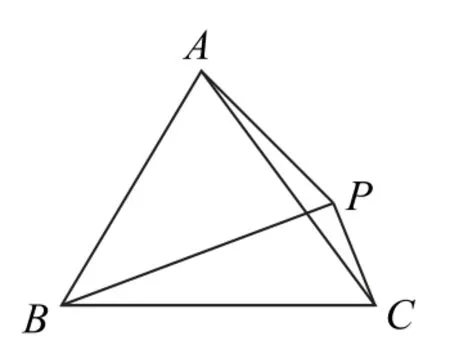
图2

2 典例精析

2.1 图像与性质

例1 函数y＝Asin(ωx＋φ)(A,ω＞0,图像的一部分如图3 所示,求其解析式.

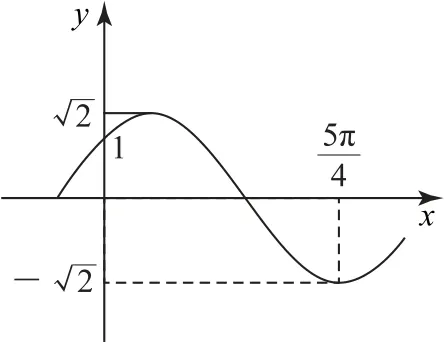
图3

图4

2.2 三角求值

1)乘积倍角化

例3 求sin6°sin42°sin66°sin78°的值.

方法1 应用二倍角正弦公式化倍角形成分式约分求值.

方法2 应用三倍角公式化倍角形成分式约分求值.

所以数列{f(n)}的特征方程①就是0,由此得递推算法:

3)构造方程求值

4)复数方法

2.3 反三角函数

2.4 不等式与最值

2.5 复合最值

2.6 恒成立问题中的极端性思维方法

例19f(x)＝1－acosx－bsinx－Acos2x－Bsin2x,其中a,b,A,B∈R,如果对一切x∈R,都有f(x)≥0.求证:

(1)a2＋b2＋A2＋B2≤3;

(2)f(x)≤3.

2.7 三角与几何

例20 如图5 所示,点P在△ABC内部,并且

图5

∠ABP＝30°,

∠CBP＝∠BCP＝24°,

∠ACP＝54°,

求∠BAP.

设∠BAP＝x,且为锐角,则∠PAC＝48°－x.由塞瓦定理得

则

取倒数得

则tanx＝tan18°,所以x＝18°,故∠BAP＝18°.

例21 如图6 所示,直线OP的倾斜角是30°,线段|OP|＝1,过点P作直线l分别交x轴、y轴于点M,N,由点M,N,求f＝|OM|＋|ON|－|MN|的最大值.

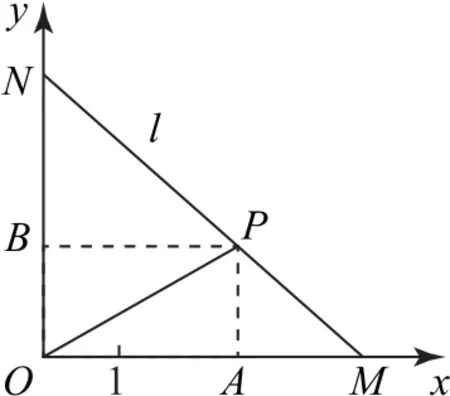
图6

(完)