高中数学平面向量中取值范围问题的求解策略探究

顾志国

(江苏省宿迁市泗洪县第一高级中学)

平面向量的数量积是高中数学中的一个核心知识点,常与平面几何、三角函数、解三角形、解析几何等综合考查,题目形式多种多样,其中求向量的数量积和模的取值范围问题就是典型的一种.为帮助同学们系统掌握这种问题常用的解题策略,本文以几道典型的例题为例介绍一些常用的解题方法.

1 利用参数的取值范围

用参数表示某些线段上的动点是解决有关向量问题的常用方法,此时的参数是有范围限制的,利用好该范围是求向量数量积取值范围的重要依据.

例1 在矩形ABCD中,边AB,AD的长分别为2,1,若M,N分别是边BC,CD上的点,且满足的取值范围.

分别以矩形的边AB,AD为x轴 和y轴建立如图1所示的平面直角坐标系,则B(2,0),C(2,1).设

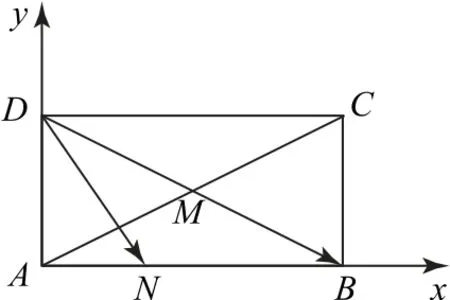
图1

则M(2,λ),N(2－2λ,1),所以

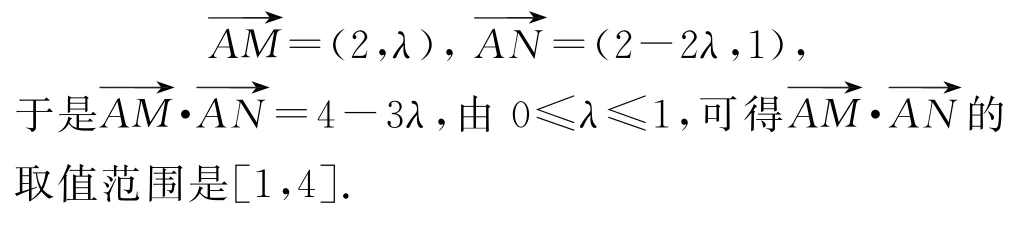
本题先用参数λ将两个动点M,N的坐标表示出来,进而可得出所求向量的数量积,解题时需注意到参数λ的取值范围直接影响到所求向量数量积的取值范围.

例2 在直角梯形ABCD中,AB//DC,∠ABC＝90°,AB＝3,BC＝DC＝2.若E,F分别是线段DC和BC上的动点,求的取值范围.

如图2所示,在直角梯形ABCD中,分别以AB,BC所在的直线为x轴和y轴建立平面直角坐标系,由已知可得A(－3,0),C(0,2),D(－2,2),则＝(3,2).

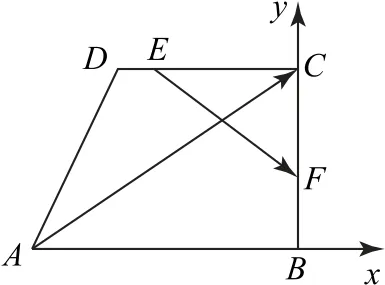
图2

由于本题中有两个动点,故需要设两个变量,在确定这两个变量的取值范围后,就可以运用不等式的性质解决两个变量的线性关系的取值范围问题.

2 利用二次函数

通过建立平面直角坐标系,可以运用坐标很快地将有关向量用含参变量表示出来,这样向量的数量积问题可能能转化为关于参数的二次函数问题,从而利用二次函数的性质解题就顺其自然了.

例3 在等腰直角△ABC中,∠ABC＝90°,AB＝BC＝2,M,N为AC边上的两个动点(M,N不与A,C重合),且满足,求的取值范围.

不妨设点M靠近点A,点N靠近点C,以等腰直角△ABC的直角边所在直线为坐标轴建立如图3 所示的平面直角坐标系,则A(0,2),C(2,0),线段AC的方程为x＋y－2＝0(0≤x≤2).

图3

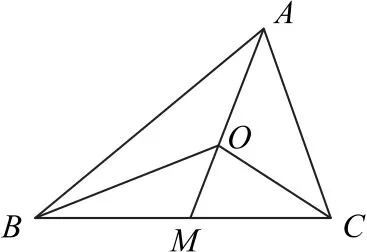
图4

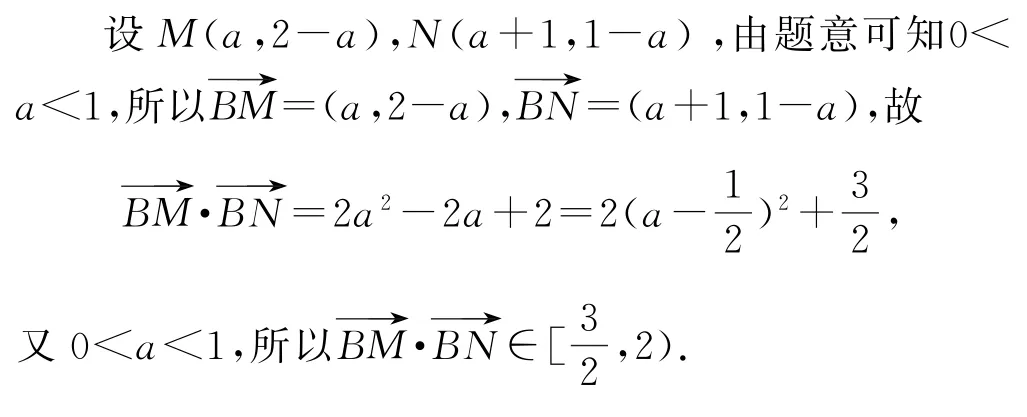
由于求出的向量数量积是一个关于参数a的二次函数,于是利用二次函数求最值的方法,根据参数的范围确定向量数量积的取值范围便是顺理成章的事.

本解法虽然没有建立平面直角坐标系求解,但灵活运用了共线向量的定理,通过引入参数将待求的向量数量积用已知向量进行替换变形,进而将原问题转化为二次函数求最值问题.

3 利用三角函数

许多与圆上动点有关的向量问题,通常先设出该动点的坐标,再利用三角函数的性质解题.

例5 已知正方形ABCD的边长为2,点E为AB的中点.以A为 圆心、AE为 半径,作弧 交AD于

点F.若P为劣弧EF上的动点,求的取值范围.

如图5 所示,分别以AB,AD所在直线为x轴、y轴 建 立 平 面 直 角 坐 标系,由于正方形ABCD的边长为2,则C(2,2),D(0,2),由于P为弧EF上的动点,不妨设

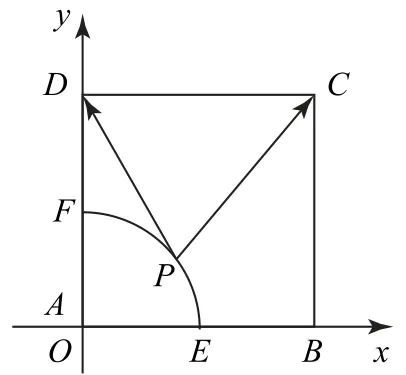
图5

通过建立平面直角坐标系求解本题是比较容易想到的一种方法,设出动点P的坐标,所求向量的数量积便可通过三角函数表示出来,进而可将原问题转化为三角函数的取值范围问题.

例6 半径为2的扇形的圆心角为120°,M,N分别为线段OP,OQ的中点,A为上任意一点,求的取值范围.

如图6 所示,以点O为 坐 标 原 点、OQ所在直线为x轴建立平面直角坐标系,则

图6

因为扇形可看成圆的一部分,所以通过设角θ为参数,就可以将向量的数量积用三角函数关系式表示出来,后续便可利用三角函数的有界性解题.

本文总结了求平面向量数量积取值范围问题的几种常规方法,可能不够全面,在具体问题中可能还会有其他奇思妙解,限于篇幅,这里就不赘述了.

(完)