巧构平面向量 妙解数学问题

杜银玲

(江苏省泰州市姜堰区娄庄中学)

平面向量作为高中数学的重要内容,它不仅具有一套完整的知识体系,更是解数学题的有力工具.无论是代数问题,还是几何问题,均可考虑用平面向量知识求解,下文举例说明.

1 妙解三角函数求值问题

对于某些三角函数式求值问题,可以通过构造坐标系,利用向量的运算求解.在求解时,可能需要用到三角恒等变换公式.

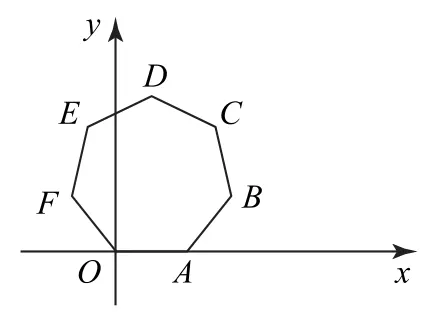
图1

解答本题用到了平面向量运算的两个性质:1)|m•n|≤|m||n|;2)几个首尾相连的向量之和为零向量.

2 妙解平面几何问题

例2 如图2所示,在平行 四 边 形ABCD中,BC＝2BA＝2,∠ABC＝60°,作AE⊥BD交BC于点E,求证:BE∶EC＝2∶3.

图2

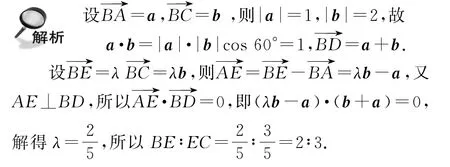
利用平面向量求解平面几何问题,通常有两种方法:基底法和坐标法.当给出的图形易于建立平面直角坐标系时,一般采用坐标法.本例中采用了基底法,也可采用坐标法,读者可自行尝试.

3 妙解不等式问题

平面向量数量积运算的性质和向量形式的三角不等式都具备不等式的特征,巧妙构造向量并利用这些向量知识有时可以快速解决不等式问题.例3 如图3所示,已知凸五边形ABCDE内接于半径为1的圆,且AB＝a,BC＝b,CD＝c,DE＝d,AE＝2,求证:

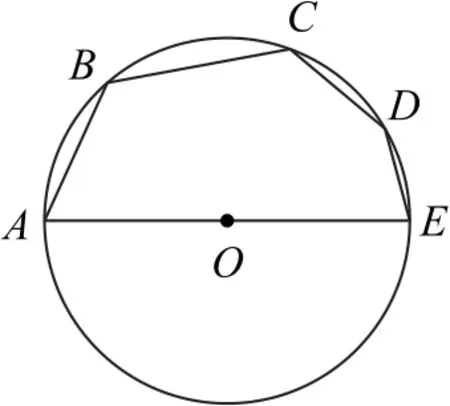
图3

连接AC,CE,易知

4 妙解解析几何问题

平面向量是沟通几何与代数的桥梁,因此可以利用该知识点解决平面向量与解析几何的综合题.

图4

通过对以上几类问题的分析,不难看出平面向量在解题中的应用.其实,利用平面向量还可以证明三角恒等变换公式、正弦定理、余弦定理以及解析几何中的点到直线的距离公式等,限于篇幅,这里不再展开,感兴趣的读者可以尝试证明.

(完)