平面向量问题的致错根源剖析

尹春晨

(福建省永安市第九中学)

高考对平面向量的考查主要涉及平面向量的基本概念、一些特殊的向量(如零向量、单位向量)、向量的关系(相等、相反)、向量的夹角、向量的运算、向量的模等,学生在解题中极易出现因对概念把握不准确、混淆向量的投影与投影向量、忽视向量夹角的定义、不注意向量夹角的取值范围等问题造成错解.下面针对这些致错根源进行举例剖析.

1 对基本概念把握不准确

例1 现有如下四个命题:

①已知向量a,b,则“a＝b”是“|a|＝|b|”的充要条件;

②已知向量a,b是两个单位向量,则“a＝b”是“|a＋b|＝2”的充要条件;

③若a•b＝0,则a＝0或b＝0;

④若a//b且b//c,则a//c.

其中正确的命题为_________.

错解 此类问题综合了向量的有关概念,若对相关概念把握不准确,则易错选①③④.

剖析 对于命题①,向量是既有大小又有方向的矢量,当a＝b时,两向量的模相等,方向相同,但两个模相等的向量,方向不一定相同,故“a＝b”是“|a|＝|b|”的充分不必要条件,命题①错误.

对于命题②,|a＋b|≤|a|＋|b|,当且仅当两个向量同向时,等号成立,命题②正确.

对于命题③,若向量a≠0且b≠0,当a⊥b时,a•b＝0,命题③错误.

对于命题④,若b＝0,则a//b且b//c,但向量a,c不一定平行,命题④错误.

综上,正确的命题为②.

2 混淆向量的投影与投影向量

3 忽视向量夹角的定义

例3 在△ABC中＞0,则△ABC的形状是( ).

A.锐角三角形 B.直角三角形

C.钝角三角形 D.不能确定

4 不注意向量夹角的取值范围

例4 已知a,b均为单位向量,则“|a－b|＜2”是“‹a,b›为锐角”的( ).

A.充分不必要条件

B.必要不充分条件

C.充分必要条件

D.既不充分也不必要条件

图1

5 向量的运算与数的运算不分

例5 已知向量a,b,c,现给出如下四个命题:

①a•(b＋c)＝a•b＋a•c;

②(a＋b)＋c＝a＋(b＋c);

③(a•b)c＝a(b•c);

④(a•b)2＝a2•b2.

其中正确命题的个数为________.

错解 数的运算与向量的运算是两种不同的运算,若将二者混淆,则易认为③和④正确,从而造成解题错误.

剖析 若将向量a,b换为实数,则上述几个运算关系均正确.

对于命题①,符合向量乘法的分配律,故①正确.

对于命题②,符合向量加法的结合律,故②正确.

对于命题③,两个向量的数量积运算结果为常数,则(a•b)c是与向量c共线的向量,a(b•c)是与向量a共线的向量,因此等式不一定成立,故③错误.

对于命题④,因为a•b＝|a|•|b|cos‹a•b›,所以(a•b)＝|a|•|b|cos‹a•b›,而cos‹a•b›∈[0,1],只有当cos‹a•b›＝1时,等式才成立,故④错误.

综上,正确命题①②,故正确命题的个数为2.

6 题目隐含条件利用不充分

剖析 上述解法所得结论错误的原因是求解过程中没有注意到点P在三角形的内部(含边界)这个条件.

如图2所示,设D为AB边上一点,且2,过点D作AC的平行线交BC于点E.过点E作AB的平行线交AC于点F.

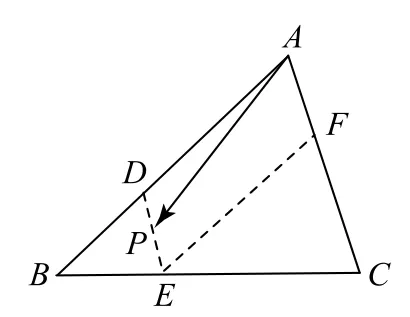
图2

当然,在求解与向量有关的问题时易出错的地方还有很多,如在利用向量三角形法则或平行四边形法则进行转化时,未注意向量的方向,在对已知关系进行变形时,未对变形的等价性进行判断等.总之,同学们在学习中要注意对这些易错点进行归纳,对错误根源进行剖析,避免同类错误屡次出现.

(完)